H. Kurke

Die Schnitt-Theorie (engl. intersection theory) ist zentraler Bestandteil der algebraischen Geometrie seit ihren Ursprüngen (z. B. Bezouts Theorem über den Durchschnitt ebener Kurven, 1720 durch MacLaurin formuliert, um 1760 durch Bezout und durch Euler bewiesen). Hilberts 15. Problem (1900) ist diesem Thema gewidmet und fordert eine rigorose Begründung von Schuberts abzählendem Kalkül (H. Schubert, Kalkül der abzählenden Geometrie, Leipzig 1879). Nach langen und z. T. kontroversen Diskussionen über eine geeignete lokale Definition für die Vielfachheit einer irreduziblen Komponente des Durchschnittes von zwei UnterVarietäten in einer Varietät X war um 1960 für quasiprojektive Varietäten eine befriedigende algebraische Theorie etabliert (A. Weil, P. Samuel, M. Nagata, W.L Chow, J.P. Serre und andere). Es wird für jede solche Varietät ein Schnittring für Äquivalenzklassen algebraischer Zyklen in zwei Schritten konstruiert:

(1) Für algebraische Zyklen \begin{eqnarray}z=\displaystyle \sum {n}_{j}{V}_{j},\,\,{z}^{^{\prime} }=\displaystyle \sum {n}_{k}^{^{\prime} }{V}_{k}^{^{\prime} }\end{eqnarray} der Kodimension p, q, die sich eigentlich schneiden (d. h., jede irreduzible Komponente W von \(({\cup }_{j}{V}_{j})\cap (\mathop{\cup }\limits_{k}\,{V}_{k}^{^{\prime} })\) hat die erwartete Kodimension p + q), wird ein algebraischer Zyklus \begin{eqnarray}z\cdot {z}^{^{\prime} }=\displaystyle \sum _{j,k}{n}_{j}{n}_{k}^{^{\prime} }\left(\displaystyle \sum _{W}i(W,{V}_{j}\cdot {V}_{k}^{^{\prime} };X)W\right)\end{eqnarray} definiert, wobei W alle irreduziblen Komponenten von V_j ∩ V_k durchläuft, und die Schnittmultiplizität \begin{eqnarray}i(W,{V}_{j}\cdot {V}_{k}^{^{\prime} };X)\in {{\mathbb{Z}}}_{\gt 0}\end{eqnarray} rein lokal definiert ist.

(2) (Moving Lemma). Es wird gezeigt, daß für je zwei rationale Äquivalenzklassen (algebraische Zyklen) α, α′ Vertreter z ∈ α, z′ ∈ α′ existieren, die sich eigentlich schneiden, und daß [z · z′] nur von den Klassen α, α′ abhängt, so daß deren Produkt durch α · α′ = [z · z′] definiert wird (oft auch als α ∪ α′ bezeichnet, in Analogie zum CupProdukt in der Topologie). Für komplexe algebraische Varietäten ist die Problematik im Rahmen der algebraischen Topologie bereits um 1925 durch S. Lefschetz studiert worden (L’ Analysis Situs et la Géométre Algébrique, 1924, und Topology, AMS Coll. Publ., 1930), und hat nicht unwesentlich die Entwicklung der algebraischen Topologie stimuliert (Zyklen-Abbildung). Um 1980 wurde ein völlig neuer Gesichtspunkt und ebenso neue Techniken entwickelt, konzeptionell einfacher, weitreichender und flexibler als die um 1960 entstandene Theorie (W. Fulton, R. MacPherson). Der neue Gesichtspunkt ist, Schnitt-Theorie nicht als Schnittring von Zyklenklassen, sondern als Theorie von Operatoren zwischen Gruppen von algebraischen Zyklen modulo rationaler Äquivalenz zu betrachten. Fundamental ist der pull-back- Operator längs einer regulären Einbettung sowie die Definition von Chern-Klassen als Operatoren. Als neue Technik dient eine von Verdier entwickelte Methode der „Deformation zum Normalenbündel“.

Die Grundzüge dieser Theorie werden im folgenden skizziert. Betrachtet werden algebraische Schemata über einem Körper, jedem solchen Schema X wird die Chow-Gruppe A_*(X) zugeordnet. Bzgl. eigentlicher Morphismen ist X ↦ A_*(X) ein Funktor, und bez. flacher Morphismen konstanter Faserdimension ein Kofunktor. Für eine abgeschlossene Einbettung i : X ⊂ Y und die komplementäre offene Einbettung j : U = X \ Y ↪ X ist die Folge \begin{eqnarray}{A}_{* }(Y)\mathop{\to }\limits^{{i}_{* }}{A}_{* }(X)\mathop{\to }\limits^{{j}^{* }}{A}_{* }(U)\to 0\end{eqnarray} exakt. Weiterhin erhält man ein äußeres Produkt \begin{eqnarray}\begin{array}{rll}{A}_{* }(X)\otimes {A}_{* }({X}^{^{\prime} }) & \to & {A}_{* }(X\times {X}^{^{\prime} })\\ [V]\otimes [W] & \mapsto & [V\times W].\end{array}\end{eqnarray}

(I) Chern-Klassen in der Schnitt-Theorie. Sie als Operatoren auf A_*(X) zu betrachten (unter einschränkenden Voraussetzungen über X durch Schnittprodukte mit bestimmten Klassen gegeben), ermöglicht ihre Einführung mit den wesentlichen Eigenschaften unter sehr allgemeinen Voraussetzungen und bringt Vereinfachungen mit sich. Die Endomorphismenringe End(A_* (X)) sind ℤ-graduiert (graduierter Ring), mit der Graduierung \({\text{End}}^{i}({A}_{* }(X))=\mathop{\times }\limits_{k-j=i}\text{Hom(}{A}_{k}\text{(}X\text{),}\,{A}_{j}\text{(}X\text{))}\).

Chern-Klassen eines Vektorbündels \( {\mathcal E} \) sind Operatoren \begin{eqnarray}(\alpha \mapsto {c}_{i}( {\mathcal E} )\cap \alpha )\in {\text{End}}^{i}({A}_{* }(X)),\,\,\,\,i\ge 1,\end{eqnarray} mit folgenden Eigenschaften:

1. (Normierung): Für \(rg\text{(} {\mathcal E} \text{)}\,\text{=}\,\text{1}\) ist \({c}_{i}\text{(} {\mathcal E} \text{)}\,\text{=}\,\text{0}\) für i > 1, und \({c}_{1}\text{(} {\mathcal E} \text{)}\,\cap [V]\text{=}\,{i}_{* }[D]\) für algebraische Varietäten i : V ⊂ X und Cartier-Divisoren D auf V mit \( {\mathcal E} \text{|}V\cong {{\mathscr{O}}}_{V}(D)\). (Hier ist [D] die zugehörige Klasse von Weil-Divisoren).

2. (Projektionsformel): Ist ϕ : X′ → X eigentlich, so ist \begin{eqnarray}{\varphi }_{* }({c}_{i}({\varphi }^{* }( {\mathcal E} ))\cap \alpha )={c}_{i}( {\mathcal E} )\cap {\varphi }_{* }(\alpha ).\end{eqnarray}

3. (Pull-back-Formel): Ist ϕ : X′ → X flach mit konstanter Faserdimension, so ist \begin{eqnarray}{c}_{i}({\varphi }^{* }( {\mathcal E} ))\cap {\varphi }^{* }\alpha ={\varphi }^{* }({c}_{i}( {\mathcal E} )\cap \alpha ).\end{eqnarray}

4. (Additivität): Mit \(c\text{(} {\mathcal E} \text{)}\,=:\,1+{c}_{1}\text{(} {\mathcal E} \text{)}+{c}_{2}\text{(} {\mathcal E} \text{)}\,\text{+}\cdots \) gilt für exakte Folgen 0 → ℰ′ → ℰ → ℰ″ → 0 die Whitney-Formel c(ℰ) = c(ℰ′)c(ℰ′).

Für Bündel vom Rang 1 ist \(c\text{(} {\mathcal E} \text{)}\) durch 1. festgelegt, und 2., 3. sind direkte Folgen dieser Definition, ebenso die Tatsache, daß die Chern-Klassen von Geradenbündeln miteinander vertauschbare Operatoren sind und c₁ ein Gruppenhomomorphismus \begin{eqnarray}\text{Pic}(X)\to {\text{End}}^{1}({A}_{* }(X))\end{eqnarray} in die Picard-Gruppe ist. Außerdem kann man die Chern-Klasse \({c}_{1}\text{(} {\mathcal L} \text{)}\) wie folgt lokalisieren: Wenn \(\lambda : {\mathcal L} \to {{\mathscr{O}}}_{X}\) ein Schnitt von \(\mathop{{\mathscr{L}}}\limits^{\vee }={{\mathscr{L}}}^{-1}\) mit dem Nullstellenschema i : Z(λ) = Z ↪ X ist, so ist \({c}_{1}({\mathscr{L}})\cap \alpha \in {i}_{* }{A}_{* }(Z)\). Letzteres besitzt folgende Verallgemeinerung (durch Induktion nach r, unter Verwendung der Projektionsformel): Besitzt ℰ eine Filtration \begin{eqnarray} {\mathcal E} ={ {\mathcal E} }_{r}\supset { {\mathcal E} }_{r-1}\supset \cdots \supset { {\mathcal E} }_{1}\subset { {\mathcal E} }_{0}=0\end{eqnarray} so, daß \({ {\mathcal E} }_{i}/{ {\mathcal E} }_{i-1}={ {\mathcal L} }_{i}\) Geradenbündel sind, so gilt für jedes \(\lambda : {\mathcal E} \to {{\mathscr{O}}}_{X}\) mit dem Nullstellenschema Z = Z(λ) ↪ X die Inklusion \begin{eqnarray}{c}_{1}({{\mathscr{L}}}_{1}),\ldots,{c}_{1}({{\mathscr{L}}}_{r})\cap \alpha \in {i}_{* }A(Z)\end{eqnarray} (also \({c}_{1}({ {\mathcal L} }_{\text{1}}),\ldots,{c}_{1}({ {\mathcal L} }_{r})=0\), wenn Z = φ). Für höheren Rang r > 1 betrachtet man \(P={\mathbb{P}}\text{(} {\mathcal E} \text{)}\mathop{\to }\limits^{p}X\). p ist eigentlich und flach mit den Fasern ℙ^r−1. Dann ist \begin{eqnarray}\begin{array}{rrlr}{p}_{* }({c}_{1}{({{\mathscr{O}}}_{ {\mathcal E} }(1))}^{j}\cap {p}^{* }\alpha ) & = & 0 & j\lt r-1\\ {p}_{* }({c}_{1}{({{\mathscr{O}}}_{ {\mathcal E} }(1))}^{r-1}\cap {p}^{* }\alpha ) & = & \alpha. & \end{array}\end{eqnarray}

Man definiert Operatoren \({s}_{j}( {\mathcal E} )\in {\mathrm{End}}^{j}({A}_{* }(X))\) (Segre-Klassen) durch \begin{eqnarray}{s}_{j}( {\mathcal E} )={(-1)}^{j}{p}_{* }({c}_{1}{({{\mathscr{O}}}_{ {\mathcal E} }(1))}^{r-1+j}\cap {p}^{* }\alpha )\end{eqnarray} und \begin{eqnarray}\begin{array}{lll}c( {\mathcal E} ) & = & {(1+{s}_{1}( {\mathcal E} )+{s}_{2}( {\mathcal E} )+\cdots )}^{-1}\\ & = & 1+{c}_{1}( {\mathcal E} )+{c}_{2}( {\mathcal E} )+\cdots \end{array}\end{eqnarray}

Es läßt sich zeigen, daß die so definierten Klassen die Bedingungen 1. bis 4. erfüllen und durch diese Eigenschaften charakterisiert sind, außerdem folgt \({c}_{i}({\mathscr{E}})=0\) für \(i\gt rg({\mathscr{E}})\), und Operatoren \({c}_{i}({\mathscr{E}})\), \({c}_{j}({\mathscr{F}})\) sind miteinander vertauschbar.

Diese Eigenschaften werden mit dem sogenannten Splittingprinzip bewiesen: Sind \({ {\mathcal E} }_{\text{1}},\ldots,{ {\mathcal E} }_{k}\) Vektorbündel auf X, so gibt es einen flachen eigentlichen Morphismus \({X}^{\prime}\mathop{\to }\limits^{f}X\) konstanter Faserdimension, für den gilt:

(a) f* : A_*(X) → A_*(X′) ist injektiv.

(b) Jedes Bündel \({f}^{* }{{\mathscr{E}}}_{v}\) besitzt eine Filtration mit Geradenbündeln als Subquotienten.

Eine Filtration von \({\mathscr{E}}\) mit Subquotienten \({{\mathscr{L}}}_{i}\) (lokal frei vom Rang 1) liefert eine solche von \({p}^{* }{\mathscr{E}}\otimes {{\mathscr{O}}}_{{\mathscr{E}}}(-1)\) (für \(p:P={\mathbb{P}}({\mathscr{E}})\to X\)) mit Subquotienten \({p}^{* }{{\mathscr{L}}}_{i}\otimes {{\mathscr{O}}}_{{\mathscr{E}}}(-1)\), und da eine Surjektion \({p}^{* }{\mathscr{E}}\otimes {{\mathscr{O}}}_{{\mathscr{E}}}(-1)\to {{\mathscr{O}}}_{p}\) existiert, gibt es in End(A_*(P)) die Relation \begin{eqnarray}\displaystyle \prod _{v=1}^{r}(\eta -\tilde{{\lambda }_{v}})=0\end{eqnarray} mit \(\eta ={c}_{1}({{\mathscr{O}}}_{{\mathscr{E}}}(1))\) und \({\tilde{\lambda }}_{v}={c}_{1}({p}^{* }{{\mathscr{L}}}_{v})\). Mittels Projektionsformel und Definition von \(c({\mathscr{E}})\) folgt daraus mit \({\lambda }_{v}={c}_{1}({{\mathscr{L}}}_{v})\): \begin{eqnarray}\begin{array}{lll}c( {\mathcal E} ) & = & \displaystyle \prod _{v=1}^{r}(1+\lambda v)\\ {c}_{j}( {\mathcal E} ) & = & {\sigma }_{j}({\lambda }_{1},\ldots,{\lambda }_{r}),\end{array}\end{eqnarray} wobei σ_j die j-te elementarsymmetrische Funktion ist. Das Splittingprinzip, zusammen mit Projektionsformel und Pull-back-Formel, ergibt dann Additivität, \({c}_{j}( {\mathcal E} )=0\) für \(j\gt rg( {\mathcal E} )\), und Vertauschbar- keit, ebenso die Relation \begin{eqnarray}\begin{array}\ll{\eta }^{r}-{c}_{1}({p}^{* } {\mathcal E} ){\eta }^{r-1}+{c}_{2}({p}^{* } {\mathcal E} ){\eta }^{r-2}-\cdots +\\ {(-1)}^{r}{c}_{5}({p}^{* } {\mathcal E} )=0.\end{array}\end{eqnarray}

Weiterhin gilt: \begin{eqnarray}\begin{array}{rll}{A}_{* }{(X)}^{r} & \to & {A}_{* }(P)\\ ({\alpha }_{0},\ldots,{\alpha }_{r-1}) & \mapsto & {p}^{* }{\alpha }_{0}+\eta \cap {p}^{* }{\alpha }_{1}+\\ & & \cdots +{\eta }^{r-1}\cap p* {\alpha }_{r-1}\end{array}\end{eqnarray} ist ein Isomorphismus, und für \(\pi :{\mathbb{V}}\text{(} {\mathcal E} \text{)}\to X\) (relatives Spektrum) ist π^* : A_*(X) → A_*(V) ein Isomorphismus.

Der inverse Isomorphismus läßt sich wie folgt beschreiben: Ist \(Q={\mathbb{P}}({\mathscr{E}}\otimes {{\mathscr{O}}}_{X})\mathop{\to }\limits^{q}X\), dann ist P ⊂ Q und V = Q \ P. Ist \({\mathscr{F}}\subset {q}^{* }({\mathscr{E}}\oplus {{\mathscr{O}}}_{X})\) das universelle Unterbündel (Kern von \({q}^{* }({\mathscr{E}}\oplus {{\mathscr{O}}}_{X})\to {{\mathscr{O}}}_{E\oplus {{\mathscr{O}}}_{X}}(1)\), so ist \(\xi \cap {A}_{* }(Q)\subseteq {i}_{* }{A}_{* }(P)\) (i : P → Q Einbettung, P Nullstellenschema eines Schnittes von \({{\mathscr{O}}}_{E\oplus {{\mathscr{O}}}_{X}}(1)\)), und somit \begin{eqnarray}{A}_{* }(Q)={q}^{* }{A}_{* }(X)+{i}_{* }{A}_{* }(P),\,\,\,\,\,\,\,\bar{\alpha }={q}^{* }\beta +{i}_{* }\gamma.\end{eqnarray}

Da \({{\mathscr{O}}}_{p}\subset {\mathscr{F}}|P\) als Unterbündel, ist \({c}_{r}({\mathscr{F}}|P)=0\), also \({c}_{r}({\mathscr{F}})\cap {i}_{* }{A}_{* }(P)=0\). Nach der Whitney-Formel ist \begin{eqnarray}{c}_{r}({\mathscr{F}})=\displaystyle \sum _{j+k=r}{(-1)}^{k}{c}_{j}({q}^{* } {\mathcal E} ){\xi }^{k}\end{eqnarray} und somit \begin{eqnarray}{q}_{* }({c}_{r}({\mathscr{F}})\cap \bar{\alpha })=\displaystyle \sum _{j+k=r}{(-1)}^{k}{c}_{j}( {\mathcal E} )\cap {q}_{* }({\xi }^{k}\cap {q}^{* }\beta )=\beta \end{eqnarray} und \begin{eqnarray}{\pi }^{* }(\beta )={j}^{* }({q}^{* }\beta )={j}^{* }(\bar{\alpha }-{i}_{* }(\gamma ))=\alpha.\end{eqnarray}

(II) Reguläre Einbettungen und die fundamentale Konstruktion. Reguläre Einbettungen i : Y ↪ X der Kodimension d sind abgeschlossene Einbettungen, deren Idealgarbe lokal durch eine reguläre Folge der Länge d definiert wird (für d = 1 sind dies also die effektiven Cartier-Divisoren). Die zugehörige Konormalengarbe \({{\mathscr{N}}}_{X|Y}^{* }\) (Normalenbündel) ist lokal frei vom Rang d, \begin{eqnarray}{N}_{X|Y}={\mathbb{V}}({{\mathscr{N}}}_{X|Y}^{* })\mathop{\to }\limits^{\pi }X\end{eqnarray} (relatives Spektrum) ist das zugehörige Normalenbündel.

Für jeden Morphismus f : Y′ → Y und X′ = f⁻¹(X) ⊂ Y erhält man dann Homomorphismen i^! : A_k(Y′) → A_k−d(X′), \begin{eqnarray}{i}^{!}\cdot \left(\displaystyle \sum _{i}{n}_{i}[{V}_{i}]\right)=\displaystyle \sum _{i}{n}_{i}X\cdot {V}_{i},\end{eqnarray} wobei X · V wie folgt definiert ist: Wenn W = V_×YX = f⁻¹(X) ⊂ V, so ist der Normalenkegel C_W|V rein k-dimensional und abgeschlossenes Unterschema des Vektorbündels \(N=W{\times }_{X}{N}_{X|Y}\mathop{\to }\limits^{\pi }W\). Also ist nach (I) die Zyklenklasse [C_W|V] ∈ A_k (N) von der Form \begin{eqnarray}[{C}_{W|V}]={\pi }^{* }\alpha,\,\,\,\,\,\alpha \in {A}_{k-d}(W),\end{eqnarray} und X · V wird als Bild von α in A_k−d(X′) definiert.

Die wichtigsten Eigenschaften dieser Konstruktion sind die folgenden: Bzgl. einer Zerlegung \begin{eqnarray}f=g\circ \varphi :{Y}^{\prime}\mathop{\to }\limits^{\varphi }{Y}^{\prime\prime}\mathop{\to }\limits^{g}Y\end{eqnarray} mit den durch g, ϕ bzw. i induzierten Abbildungen h : X″ → X, ψ : X′ → X″ bzw. i″ : X″ → Y″ gilt:

(a) (Push-forward): Wenn ϕ eigentlich ist, so ist i^! ∘ ϕ_* = ψ_* ∘ i^!.

(b) (Pull-back): Wenn ϕ flach und von konstanter Faserdimension ist, so auch ψ und i^! ∘ ϕ^* = ψ^* ∘ i^!.

(c) (Exzeß-Schnittformel): Wenn i″ ebenfalls reguläre Einbettung ist, so ist \({{\mathscr{N}}}_{{X}^{\prime\prime}|{Y}^{\prime\prime}}\) ein Unterbündel von \({f}^{* }{{\mathscr{N}}}_{X|Y}\), also \({\mathscr{E}}={f}^{* }{{\mathscr{N}}}_{X|Y}/{{\mathscr{N}}}_{{X}^{\prime\prime}|{Y}^{\prime\prime}}\) ein Vektorbündel (Exzeß-Normalenbündel), und \begin{eqnarray}{i}^{!}(\alpha )={c}_{e}({\psi }^{* }\varepsilon )\cap {i}^{\prime\prime!}(\alpha )\end{eqnarray}\((e=rg({\mathscr{E}}))\). Beispielsweise gilt für Morphismen h : Y′ → X und f = i ∘ h : Y′ → X die Formel \({i}^{!}(\alpha )={c}_{d}({h}^{* }{{\mathscr{N}}}_{X|Y})\cap \alpha \).

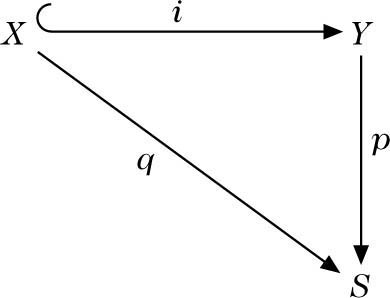
(d) (Verträglichkeit mit Pull-back): Für kommutative Diagramme mit regulärer Einbettung i,

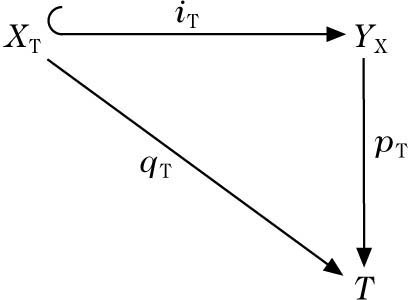
und daraus durch Basiswechsel T → S induzierte Diagramme

gilt: Wenn p, q flach mit konstanter Faserdimension sind, so auch PT, qT und \({p}_{T}^{* }={i}^{!}\circ {p}_{T}^{* }\). Wenn p glatt mit konstanter Faserdimension ist, und q ebenfalls reguläre Einbettung, so ist \({q}^{!}={i}^{!}\circ {p}_{T}^{* }\).

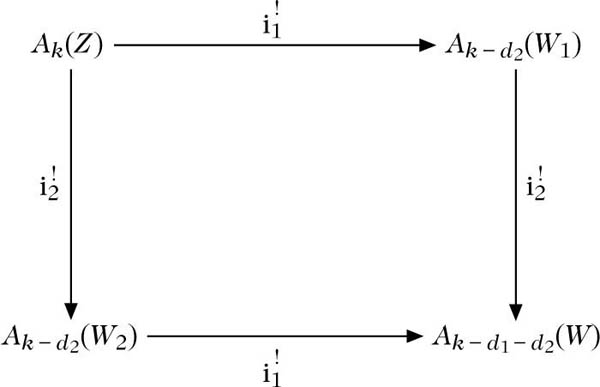
(e) (Vertauschbarkeit): Sind i₁ : X₁ → Y₁i₂ : X₂ → Y₂ reguläre Einbettungen der Kodimension d₁ bzw. d₂, und f_v : Z → Y_v Morphismen, \begin{eqnarray}Z\supseteq {W}_{v}={f}_{v}^{-1}({X}_{v})\supseteq W={W}_{1}\cap {W}_{2},\end{eqnarray} (v = 1, 2), so sind die Diagramme

kommutativ.

(f) (Funktorialität): Für reguläre Einbettungen i ∘ j, \(X\mathop{\to }\limits^{i}Y\mathop{\to }\limits^{j}Z\), und Morphismen \(f:{Z}^{\prime}\mathop{\to }\limits^{f}Z\) ist (j ∘ i)^! = i^! ∘ j^!.

Wichtige Beispiele für reguläre Einbettungen sind:

(a) Der Graph \(X\mathop{\to }\limits^{i}X\times Y\) eines Morphismus ϕ : X → Y in ein glattes k-Schema Y.

(b) Die Diagonaleinbettung \(X\mathop{\to }\limits^{{i}_{{\rm{\Delta }}}}X\times X\) eines glatten k-Schemas X.

Beispiel (a) liefert eine Pull-back-Abbildung ϕ^! für beliebige Morphismen ϕ : X → Y in glatte Schemata Y durch \({\varphi }^{!}(\alpha )={i}_{\varphi }^{!}([X]\times \alpha )\), α ∈ A_* (Y) mit der Eigenschaft: Für \begin{eqnarray}\varphi ={\varphi }_{1}\circ {\varphi }_{2}:X\mathop{\to }\limits^{{\varphi }_{2}}{X}_{1}\mathop{\to }\limits^{{\varphi }_{1}}Y\end{eqnarray} gilt: Wenn X₁ glatt, so \({({\varphi }_{1}\circ {\varphi }_{2})}^{!}={\varphi }_{2}^{!}\circ {\varphi }_{1}^{!}\). Wenn ϕ₂ flach von konstanter Faserdimension, so \({({\varphi }_{1}\circ {\varphi }_{2})}^{!}={\varphi }_{2}^{* }{\varphi }_{1}^{!}\). Häufig schreibt man auch ϕ* anstelle von ϕ^!. Die Kodimension bleibt unter ϕ* erhalten.

Beispiel (b) liefert ein Schnittprodukt \(\alpha \cdot \beta ={i}_{{\rm{\Delta }}}^{!}(\alpha \times \beta )\). Mit der Graduierung A*(X) durch die Kodimension (® algebraische Zyklen) wird X ↦ A*(X) ein Kofunktor auf der Kategorie glatter k-Schemata in die Kategorie der kommutativen assoziativen graduierten Ringe, das Einselement ist 1 = [X], und die Chern-Klassen sind durch \({c}_{i}({\mathscr{E}})\cap [X]\in {A}^{i}(X)\) bestimmt. (Der zugehörige Operator ist die Multiplikation mit diesem Element).

Die fundamentale Konstruktion liefert auch die lokale Schnittmultiplizität für Komponenten C von V ∩ W, in denen sich V, W eigentlich schneiden: \begin{eqnarray}{i}_{{\rm{\Delta }}}^{!}:{A}_{a+b}(V+W)\to {A}_{a+b-n}(V\cap W)\end{eqnarray} (mit n = dim X, a = dim V, b = dim W, a + b − n = dim C). Dann ist \begin{eqnarray}{i}_{{\rm{\Delta }}}^{!}([V+W])=i(C,V\cdot W;X)[C]+\cdots \end{eqnarray} (da ℤ[Δ] direkter Summand von A_a+b−n(V ∩ W)). Der Koeffizient con [C] ist die lokale Schnittmulti- plizität i(C, V · W; X).

(III) Spezialisierung zum Normalenkegel. Zu einer abgeschlossenen Einbettung X ⊂ Y erscheint die Einbettung X ⊂ C_X|Y in den Normalenkegel als Grenzfall in folgendem Sinne: Sei T = ℙ¹ ⊃ T⁰ = ℙ¹ \ {∞} und \(\sigma :\tilde{M}\to Y\times T\) die Aufblasung in X × {∞}. Da X × {∞} Cartier-Divisor in X × T ist, läßt sich die Einbettung X × T ⊂ Y × T zu einer Einbettung \(X\times T\subset \tilde{M}\) liften, so daß über T⁰ die konstante Einbettung X × T⁰ ⊂ Y × T⁰ induziert wird. Über ∞ ist \({\tilde{f}}^{-1}(\infty )=\tilde{Y}\cup E\), \(\tilde{Y}\to Y\) Aufblasung in X, und E der exzeptionelle Divisor der Aufblasung.

Ist \(M=\tilde{M}\backslash \tilde{Y}\), \(f=\tilde{f}|M\), so ist f⁻¹(∞) = C_X|Y der Normalenkegel. Also erhält man eine flache Familie von Einbettungen

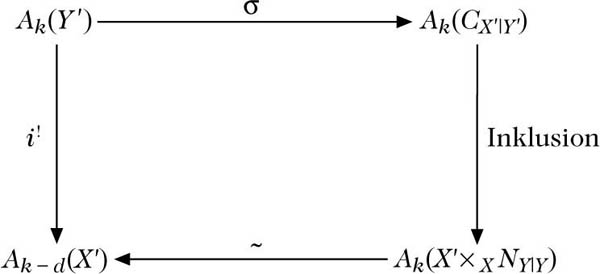
die über T⁰ = T \ {∞} die gegebene Einbettung, und über ∞ die Einbettung X ⊂ C = C_X|Y ist. C = f⁻¹(∞)) ist ein Cartier-Divisor auf M, und \({{\mathscr{O}}}_{M}(C)\simeq {f}^{* }{{\mathscr{O}}}_{T}(1)\). Das ermöglicht die Definition von Spezialisierungshomomorphismen σ : A_* (Y) → A_*(C) mit der Eigenschaft \begin{eqnarray}\sigma ([V])=[{C}_{V\cap X|V}]\in {A}_{* }(C)\end{eqnarray} für Varietäten V ⊂ Y.

Für die Einbettung i : C ⊂ M ist nämlich \({{\mathscr{O}}}_{M}(C)\otimes {{\mathscr{O}}}_{C}\simeq {{\mathscr{O}}}_{C}\), also ist i^! auf i_*A_* (C) ⊂ A_* (M) trivial, und \begin{eqnarray}{A}_{k+1}(M)/{i}_{* }{A}_{k+1}(C)\underset{{j}^{* }}{\overset{\sim }{\to }}{A}_{k+1}(M\backslash C)\underset{{p}^{* }}{\overset{\sim }{\leftarrow }}{A}_{k}(Y)\end{eqnarray} (da \(M\backslash C\simeq Y\times {T}^{0}=Y\times {{\mathbb{A}}}^{1}\)). Zusammen mit diesen Isomorphismen induziert also i^! einen Homo-morphismus σ : A_*(Y) → A_*(C), der auf Klassen von Varietäten die oben angegebene Abbildung ist. Die Abbildungen i^! in (II) sind damit wie folgt definiert:

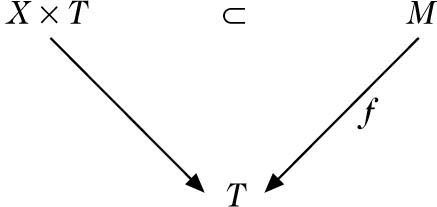
(IV) Bivariate Schnitt-Theorie. Chern-Klassen (I) und die fundamentale Konstruktion (II) sind Spezialfälle einer bivariaten Schnitt-Theorie A^*(X → S) für Morphismen X → S. Für jedes S-Schema T → S in der betrachteten Kategorie algebraischer k-Schemata sei X_T = X ×_ST. Die Elemente von A^p(X → S) sind Familien von Operatoren \begin{eqnarray}{c}_{T}\in {\text{Hom}}^{p}({A}_{* }(T),{A}_{* }({X}_{T})))=\\ \,\,\,\,\,\,\,\displaystyle \prod _{k}\text{Hom}({A}_{k}(T),{A}_{k-p}({X}_{T})),\end{eqnarray} für jedes solche T → S.

Beispiele: (1) Chern-Klassen \({c}_{p}( {\mathcal E} )\) sind aus \({A}^{p}(X\mathop{\to }\limits^{id}X)\).

(2) Für reguläre Einbettungen \(X\mathop{\hookrightarrow }\limits^{i}Y\) ist \({i}^{!}\in {A}^{d}(X\mathop{\hookrightarrow }\limits^{i}Y)\) (d = Kodimension).

(3) A^−k(X → pt) = A_k(x).

Wenn X → S′ → S eine Zerlegung von X → S ist, gibt es ein offensichtliches Produkt \begin{eqnarray}{A}^{p}(X\to {S}^{\prime})\otimes {A}^{q}({S}^{\prime}\to S)\to {A}^{p+q}(X\to S),\end{eqnarray} und wenn \(X\mathop{\to }\limits^{\varphi }Y\to S\) eine Zerlegung mit einem eigentlichen Morphismus ϕ ist, erhält man einen Push-forward Homomorphismus \begin{eqnarray}{\varphi }_{* }:{A}^{p}(X\to S)\to {A}^{p}(Y\to S).\end{eqnarray}

Für Morphismen g : S₁ → S und X₁ = X ×_S S₁ erhält man einen Pull-back Homomorphismus \begin{eqnarray}{g}^{* }:{A}^{p}(X\to S)\to {A}^{p}({X}_{1}\to {S}_{1}).\end{eqnarray}

Auf diese Weise wird \begin{eqnarray}{A}^{* }(X)={A}^{* }(X\mathop{\to }\limits^{id}X)\end{eqnarray} zu einem assoziativen Ring mit Einselement und X ↦ A*(x) ein Kofunktor, und A_*(X) = A*(X → pt) wird zu einem A*(X)-Modul.

Für glatte X liefert A*(X) → A*(X)c ↦ c([X]) einen Isomorphis, so daß das Produkt dem Schnittprodukt entspricht.