Aussage der elementaren Geometrie.

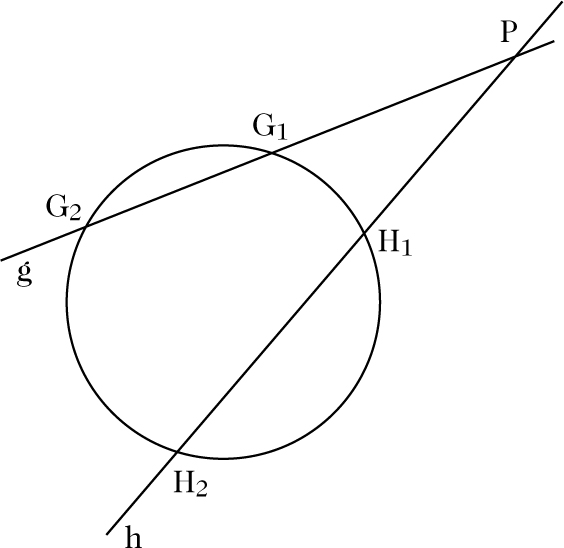
Gegeben sei ein Kreis K und ein außerhalb dieses Kreises liegender Punkt P. Weiter seien zwei Geraden g und h gegeben, die sich in P schneiden und mit K die Schnittpunkte G₁und G₂bzw. H₁und H₂haben.

Dann gilt die folgende Aussage über die Verhältnisse der Streckenlängen: \begin{eqnarray}\overline{P{G}_{1}}:\overline{P{H}_{1}}=\overline{P{H}_{2}}:\overline{P{G}_{2}}.\end{eqnarray}