stetige und isotone reellwertige Funktion einer reellen Variablen, deren Ableitung fast überall (im Lebesgue-Sinne) verschwindet, d. h. fast überall existiert und 0 ist.

Solche Funktionen haben Bedeutung bei der Frage, für welche Funktionen die Entsprechung zum Fundamentalsatz der Differential- und Integralrechnung \begin{eqnarray}\mathop{\mathop{\int}\limits^{b}}\limits_{a}{f}{^{\prime}}(x)dx=f(b)-f(a)\end{eqnarray} für das Lebesgue-Integral gilt. Hierbei seien −∞ < a < b < ∞ und f : [a, b] ℝ. Ist f nur fast überall differenzierbar, so geht man bei dieser Notierungsweise stillschweigend davon aus, daß f′ auf der Ausnahmemenge (beliebig) ergänzt ist.

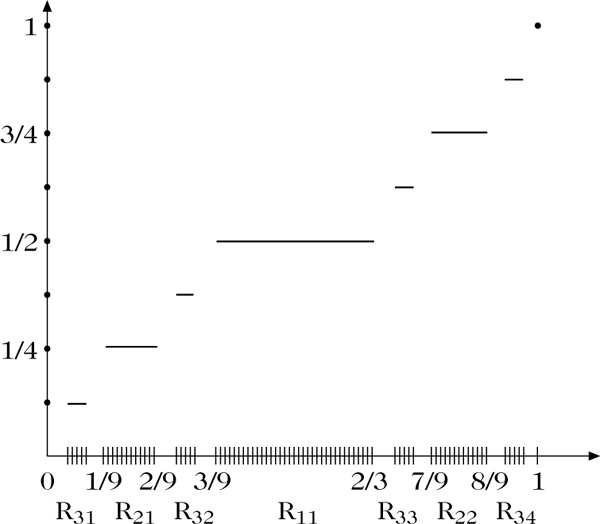
Ein isotones f ist fast überall differenzierbar, die Ableitung ist Lebesgue-integrierbar, und man hat \begin{eqnarray}\mathop{\mathop{\int}\limits^{b}}\limits_{a}{f}{^{\prime}}(x)dx\le f(b-)-f(a+).\end{eqnarray} Daß für eine stetige isotone Funktion tatsächlich „<“ auftreten kann, zeigt das auf Georg Cantor zurückgehende Standardbeispiel der Cantor- Funktion, die auch Lebesgue-singuläre Funktion genannt wird: Man geht aus von der Cantor- Menge \begin{eqnarray}G:=\mathop{\mathop{\bigcap}\limits^{\infty}}\limits_{k=0}{I}_{k},\end{eqnarray} wobei I₀ := [0, 1] und I_k für k ∈ ℕ disjunkte Vereinigung von 2^k abgeschlossenen Intervallen der Länge 3^−k ist, die aus den Intervallen aus I_k−1 durch Entfernen der offenen mittleren Drittel entstehen. Für k ∈ ℕ seien \({R}_{k{,}_{k}}\) für κ = 1,…,2^k−1 die beim Übergang von I_k−1 zu I_k entfernten offenen Intervalle (von links nach rechts gezählt), und damit \begin{eqnarray}h(x):=\frac{2\kappa -1}{{2}^{k}}\,\,(x\in {R}_{k{,}_{k}};\kappa =1,\mathrm{\ldots},{2}^{k-1}).\end{eqnarray}h ist dann isoton auf K := [0, 1] \ C. (Auf jedem offenen Intervall \({R}_{k{,}_{k}}\) erhält h das arithmetische Mittel seiner Werte auf den beiden benachbarten Intervallen, auf denen h schon definiert ist.)

Durch f(₀) := 0 und \begin{eqnarray}f(x):=\sup \{h(t)|K\,\unicode {8717}\,t\lt x\}\quad (x\in C\backslash \{0\})\end{eqnarray} wird h fortgesetzt zu einer stetigen isotonen Funktion f mit f([0, 1]) = [0, 1], f′(x) = 0 (x ∈ K), also f′(x) = 0 fast überall, und somit \begin{eqnarray}\mathop{\mathop{\int}\limits^{1}}\limits_{0}{f}{^{\prime}}(x)dx=0\lt 1=f(1)-f(0).\end{eqnarray}

Für x ∈ C existiert eine Darstellung \begin{eqnarray}\mathop{\sum ^{\infty}}\limits_{v=1}\frac{2{x}_{v}}{{3}^{v}}\quad \text {mit}\quad {x}_{v}\in \{0, 1\},\end{eqnarray} und dafür gilt \begin{eqnarray}f(x)\mathop{\sum ^{\infty}}\limits_{v=1}\frac{{x}_{v}}{{3}^{v}}.\end{eqnarray} Das auf Riesz-Nagy zurückgehende Beispiel einer streng monotonen stetigen Funktion mit fast überall verschwindender Ableitung ist weniger anschaulich, jedoch noch deutlich frappierender.

Eine rechtsseitig stetige Funktion von beschränkter Variation ist genau dann singulär, wenn für das von ihr erzeugte signierte Maß μ gilt, daß ein N ∈ B(ℝ) so existiert, daß μ(N) = 0 und das Lebesgue-Maß von ℝ\N gleich 0 ist. Sie ist genau dann singulär stetig, falls sie singulär ist und falls in B(ℝ) bzgl. μ keine atomare Mengen liegen.

Für das Lebesgue-Integral gilt eine Entsprechung des Hauptsatzes, wenn man absolut stetige Funktionen anstelle stetiger Funktionen betrachtet.