Lexikon der Mathematik: Singulärwertzerlegung
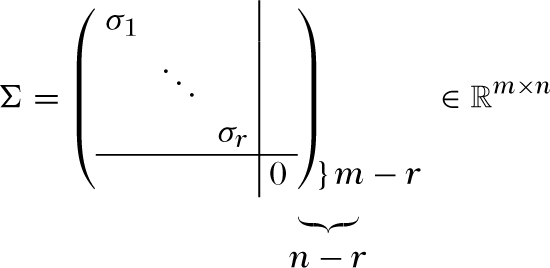
die Zerlegung einer Matrix A ∈ ℝm×n in das Produkt A = U∑VT, wobei U ∈ ℝm×m und V ∈ ℝn×m orthogonale Matrizen sind, und
die aus den von Null verschiedenen singulären Wertenσ1,…,σr von A gebildete Matrix. r ist der Rang von A.
Weiter gelten mit der Bezeichnung U = [u1, u2,…,um] und V = [v1, v2,…,vn] folgende Beziehungen:
Ein gebräuchlicher Algorithmus zur Berechnung der Singulärwertzerlegung besteht aus zwei Schritten. (Zur Vereinfachung sei m ≥ n angenommen, andernfalls betrachte man AT statt A). Im ersten Schritt wird die Matrix A durch Transformation mit Householder-Matrizen (oder Givens- Matrizen) in eine Bidiagonalgestalt überführt, d. h. in eine Matrix B, bei welcher lediglich die Dia-gonalelememte bii und die oberen Nebendiago-nalelemente bi,i+1 ungleich 0 sind. Dazu führt man abwechselnd Spalten- und Zeileneliminationen mit Householder-Matrizen (oder Givens- Rotationen) durch: Zunächst bestimmt man eine (m × m)-Householder-Matrix P1, welche die Elemente der ersten Spalte von A unterhalb des Matrixelements a11 annulliert:
mit einer (m − 1) × (n − 1)-Matrix Ã. Man behandelt nun die Matrix A auf die gleiche Weise wie à und erhält so nach n Reduktionsschritten eine (m × n)-Bidiagonalmatrix B
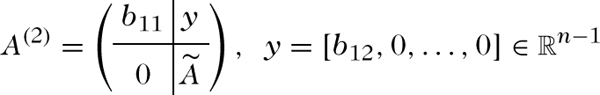
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.