Ein grundlegendes Problem der Angewandten Mathematik ist es, Objekte (beispielsweise Autokarosserien oder architektonische Konstruktionen) und Prozesse (beispielsweise Strömungsvorgänge im Windkanal) durch mathematische Modelle zu beschreiben. Dabei werden Objekte häufig durch Funktionen möglichst einfacher Struktur und Prozesse durch Differentialgleichungen beschrieben.

Für den Mathematiker ergibt sich somit das Problem, mathematische Beschreibungen für Objekte und Prozesse der realen Welt zu entwickeln und Abläufe mit Hilfe des Computers zu simulieren. Aufgaben diese Typs treten in der industriellen Fertigung (beispielsweise bei computergesteuerten Werkzeugmaschinen), in der Medizin (bei der Visualisierung von Körperorganen oder der Simulation von Krankheitsverläufen), in der Physik (Wärmeleitung, Schwingungen, Strömungsvorgänge), bei der Bildübertragung, der Signalverarbeitung und vielen anderen Gebieten auf.

Im allgemeinen können mathematische Modelle die Realität nicht exakt beschreiben, und die daraus resultierenden mathematischen Probleme sind häufig nur näherungsweise lösbar. Bei der approximativen Lösung solcher Probleme spielen Spline-funktionen, die wir unten noch näher beschreiben werden, eine zentrale Rolle. Grob gesprochen sind Splinefunktionen (kurz Splines genannt) zusammengesetzte Polynomstücke. Die einfachsten Splinekurven sind somit Streckenzüge, und die einfachsten Splineoberflächen (also Splines in zwei Variablen) bestehen aus stetig zusammengesetzten Dreiecken (Abbildung 1).

Deshalb verwendet man in der Praxis häufig Splines. Der Grundgedanke hierbei ist, daß man sich die gewünschte Flexibilität bei der Näherung komplizierter Funktionen verschaffen kann, indem man mehrere Polynomstücke eines festen vorgegebenen Grades benutzt. Dieser Grad m ist typischerweise klein, zum Beispiel zwei, drei oder vier, während andererseits die Anzahl der Polynomstücke n relativ groß ist, zum Beispiel n = 1000. Auf diese Art und Weise erhält man die benötigte große Anzahl von Freiheitsgraden, welche für gute Näherungen notwendig sind.

Genauer besteht nun ein Spline s (vom Grad m) aus Polynomstücken (vom Grad m) auf Knotenintervallen \begin{eqnarray}[k_0, k_1],[k_1, k_2],\ldots,[k_{n-1}, k_n]\end{eqnarray} der x-Achse, die an den Knoten k_i (m − 1)-mal stetig differenzierbar zusammengesetzt werden, die Funktion s entstammt also der Differenzierbarkeitsklasse C^m−1[k₀, k_n]. Falls m ≥ 2 ist, so handelt es sich um einen glatten Spline, im Fall m = 1 um einen stetigen Streckenzug.

Ein solcher Spline besitzt n + m Freiheitsgrade, während die Polynome vom Grad m nur m + 1 Freiheitsgrade besitzen. Man nennt einen derartigen Spline auch genauer einen Spline mit einfachen Knoten; ohne auf Einzelheiten einzugehen sei an dieser Stelle die Möglichkeit erwähnt, diese Definition zu verallgemeinern, indem man an den einzelnen Knoten unterschiedliche Differenzierbarkeitsordnungen vorschreibt. Man spricht dann auch von Splines mit mehrfachen Knoten, da man dies formal auch so interpretieren kann, daß eine gewisse Anzahl von Knoten k_i zu einem einzigen zusammengefaßt wird. Für Einzelheiten hierzu wird auf die weiterführende Literatur, beispielsweise [3] und [6], verwiesen.

Splines werden zur Konstruktion und Rekonstruktion (aus Meßdaten) von komplizierten Kurven verwendet. Dabei gibt man sich Punkte x₁ < … < x_n+m der x-Achse und reelle Zahlen z₁, …, z_n+m vor, und erhält durch Interpolation einen eindeutigen Spline s mit der Eigenschaft \begin{eqnarray}s(x_i)=z_i,\,\,\,i=1,\ldots,n+m.\end{eqnarray} Interpolationsprobleme dieses Typs sind allerdings im Gegensatz zum oben erwähnten Polynomfall nicht immer lösbar, vielmehr genau dann, wenn die Lagebedingung \begin{eqnarray}x_i\lt k_i \lt x_{i+m+1},\,\,\,i=1,\ldots,n-m.\end{eqnarray} gilt. Man spricht in diesem Zusammenhang von der Schoenberg-Whitney Bedingung und nennt solche Punktmengen Lagrange-Interpolationsmengen.

Diese Bedingung läßt sich durch geeignete Wahl der Knoten k_i stets erfüllen – und hierin liegt unter anderem die Stärke und Flexibilität der Splines begründet. Auf diese Weise können auch Funktionen f, beispielsweise f(x) = exp(x) (Exponentialfunktion) oder \(f(x)=\sqrt{x}\) (Quadratwurzel) mit hoher Genauigkeit approximiert werden, indem man z_i = f(x_i), i = 1, …, n + m, setzt.

Zur Berechnung der Splines müssen lineare Gleichungssysteme gelöst werden, die eine Reihe von angenehmen strukturellen Eigenschaften besitzen. Beispielsweise treten hierbei sogenannte Bandmatrizen auf.

In manchen technischen Anwendungen werden Kurven nur unter ästhetischen Gesichtspunkten konstruiert (unter Verzicht auf die exakte Darstellung). Auf dem Gebiet des Computer-Aided Design (CAD) wird folgende Methode verwendet, die wir kurz für den klassischen Fall von Polynomen beschreiben. Es soll ein Polynom q (vom Grad m) konstruiert werden, das in der Nähe von vorgegebenen Punkten \(\left(\frac{i+j}{m},{z}_{i,j}\right)\), i + j = m, in der Ebene verläuft. Zur Lösung dieser Aufgabe wird im CAD das Bernstein-Polynom \begin{eqnarray}q(x)=\displaystyle \sum _{i+j=m}{z}_{i,j}\frac{m!}{i!j!}{(1-x)}^{i}{x}^{j},\,\,\,\, x\in [0,1],\end{eqnarray} benutzt.

An dieser Darstellung von q erkennt man, daß die linearen Polynome p₁(x) = 1 − x und p₂(x) = x, welche die Werte 0 und 1 an den Randpunkten des Intervalls [0, 1] annehmen, als Bausteine verwendet werden. Für den Anwender eines interaktiven CAD-Systems besteht die Möglichkeit, die Form der zum Polynom q gehörigen Kurve durch verschiedene Wahlen der Kontrollpunkte \(\left(\frac{i+j}{m},{z}_{i,j}\right)\), i + j = m, schnell abzuändern. Analoge Ansätze sind für Splinekurven bekannt, wobei anstelle der Polynome (1 − x)_ix_j, i + j = m, die B-Splinefunktionen als Basisfunktionen verwendet werden.

Von fundamentaler Bedeutung für die eingangs genannten Anwendungsgebiete (Karosseriebau, Werkzeugmaschinen, Visualisierung von Organen, ⋯) ist die Darstellung von Oberflächen durch bivariate Splines. Dies sind Splines s(x, y) in zwei reellen Veränderlichen, welche über einem Teilbereich der Ebene festgelegt sind.

Für den Fall, daß die Splines s(x, y) auf einem Rechteck R definiert werden, kann man Tensorprodukte \begin{eqnarray}s(x,y)=s_1(x)s_2(y)\end{eqnarray} von Splines in einer Variablen verwenden. Die Theorie dieser Tensorprodukt-Splines unterscheidet sich aufgrund dieser Definition nur wenig von derjenigen der univariaten Splines und kann als weitestgehend abgeschlossen angesehen werden.

Die Probleme werden sehr viel komplexer, wenn man Splineoberflächen über allgemeineren Teilmengen der Ebene konstruieren möchte. Dies ist für vielerlei Anwendungen unumgänglich. In dieser allgemeineren Situation werden Splineoberflächen über einer Triangulierung T eines Teilbereichs der Ebene definiert (das heißt einem System von Dreiecken {T_l} wie in Abbildung 2, wobei (x, y) ∈ T).

In Analogie zu Splinekurven besteht ein bivariater Spline s(x, y) (vom Grad m) aus bivariaten Polynomstücken (vom Grad m) auf den Dreiecken T_l von T, die an den den Kanten benachbarter Dreiecke r-mal stetig differenzierbar zusammengesetzt werden.

Differenzierbarkeit ist hierbei im Sinne der beiden Variablen x und y gemeint, und als bivariates Polynom p (vom Grad m) bezeichnet man hierbei eine Funktion des Typs \begin{eqnarray}p(x,y)=\displaystyle \sum _{0\le i+j\le m}{a}_{i,j}{x}^{i}{y}^{j},\end{eqnarray} wobei a_i,j, 0 ≤ i + j ≤ m, fest vorgegebene Zahlen sind, vgl. Abbildung 3.

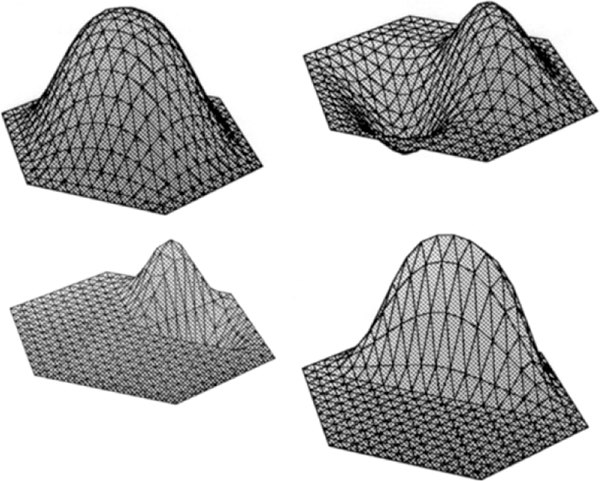
Dreiecksoberflächen wie in Abbildung 1 bestehen aus linearen (das heißt m = 1), bivariaten Polynomstücken, die entlang den Kanten nur stetig zusammengefügt werden – sie sind also nicht differenzierbar und bilden ebenso wie die oben beschriebenen Streckenzüge eine Ausnahme. Abbildung 4 zeigt Beispiele differenzierbarer bivariater Splines.

Im Gegensatz zu den Dreiecksoberflächen besitzen glatte bivariate Splines s(x, y) eine sehr komplexe Struktur, die bis heute noch nicht vollständig durchschaut wird. Hierbei treten Phänomene und mathematische Probleme auf, die in der Theorie der Splines in einer Variablen in dieser Form nicht bestehen.

Trotz beachtlicher Fortschritte seit Beginn der 80er Jahre gibt es weiterhin eine Reihe offener Fragen und ungelöster Standardprobleme in der Theorie bivariater Splines. So kennt man beispielsweise die Anzahl der Freiheitsgrade einmal differenzierbarer, bivariater Splines s(x, y) hinsichtlich einer beliebigen Triangulierung T nur, wenn der Grad größer oder gleich vier ist. Für kubische (das heißt m = 3) bivariate Splines, welche einmal differenzierbar sind, wird vermutet, daß die Anzahl der Freiheitsgrade immer einer gewissen explizit angebbaren Formel genügt – bewiesen ist diese aber bis heute nicht. Betrachtet man einmal differenzierbare bivariate Splines vom Grad Zwei, weiß man darüberhinaus, daß man im allgemeinen nur eine sehr kleine Anzahl von Freiheitsgraden erwarten darf, selbst wenn man sehr viele Dreiecke verwendet. Darüber hinaus können sich in diesem Fall Sprünge in der Anzahl der Freiheitsgrade ergeben, wenn die Gesamtgeometrie der Triangulierung eine minimale Abänderung erfährt.

Allgemein zeigt sich, daß die Struktur bivariater Splines umso komplexer wird, je näher der Grad des Splines m bei dessen Differenzierbarkeitsordnung r liegt.

Zur Analyse und Konstruktion bivariater Splines benutzt man häufig die folgende Darstellung der zugehörigen bivariaten Polynomstücke. Diese wird auch (analog dem oben angesprochenen Fall polynomialer Kurven) im CAD zur Oberflächenkonstruktion verwendet. Für vorgegebene Punkte \begin{eqnarray}\left(\frac{i+j+k}{m},{z}_{i,j,k}\right),i+j+k=m,\end{eqnarray} im Raum betrachtet man die sogenannte Bernstein-Darstellung eines bivariaten Polynoms q(x, y) (vom Grad m), \begin{eqnarray}q(x,y)=\displaystyle \sum _{i+j+k=m}{z}_{i,j,k}\frac{m!}{i!j!k!}{(1-x-y)}^{i}{x}^{j}{y}^{k},\end{eqnarray} wobei (x, y) ∈ T₀. Hierbei sind p_i(x, y) = (1−x−y), p₂(x, y) = x, und p₃(x, y) = y diejenigen bivariaten linearen Polynome, welche in zwei Eckpunkten des Dreiecks T₀ mit den Ecken (0, 0), (0, 1), (1, 0) den Wert 0, und im dritten Eckpunkt den Wert 1 annehmen. Polynomiale Oberflächen können durch verschiedene Wahlen der Kontrollpunkte \begin{eqnarray}\left(\frac{i+j+k}{m},{z}_{i,j,k}\right),i+j+k=m,\end{eqnarray} schnell entworfen und abgeändert werden. Durch Anwendung des de Casteljau-Algorithmus lassen sich bivariate Polynome effizient berechnen und visualisieren.

Durch Verwendung der Bernstein-Darstellung bivariater Polynome lassen sich Formeln angeben, die die Differenzierbarkeit für bivariate Splines über die Kanten einer Triangulierung T beschreiben. Diese werden bei der Konstruktion glatter Oberflächen durch differenzierbare bivariate Splines verwendet. Für diese Konstruktionen findet man in der klassischen Literatur der 70er Jahre zwei charakteristische Vorgehensweisen, die wir hier kurz beispielhaft beschreiben:

Abbildung 5 zeigt ein Finites Element. Es handelt sich hierbei um die Konstruktion eines bivariaten, differenzierbaren Splines vom Grad fünf. Dieser Spline s(x, y) ist durch die Vorgabe der Funktionswerte, der beiden ersten Ableitungen und der drei zweiten Ableitungen in allen Eckpunkten (dies ist im Bild durch entsprechende Kreise angedeutet) sowie der ersten orthogonalen Ableitung in den Mittelpunkten jeder Kante von T eindeutig festgelegt. Damit diese Vorgehensweise so funktionieren kann, muß man jedoch zusätzlich fordern, daß s(x, y) zweimal differenzierbar in allen Eckpunkten von T ist.

Um Splines kleinerer Grade zu verwenden, werden die gegebenen Dreiecke einer Triangulierung T oftmals weiter unterteilt. In Abbildung 6 wird diese Vorgehensweise anhand der sogenannten Clough-Tocher-Zerlegung veranschaulicht. Hierbei wird jedes Dreieck von T zunächst in drei Teildreiecke zerlegt. Man erhält so eine neue Triangulierung. Nun konstruiert man einen bivariaten differenzierbaren Spline s(x, y) vom Grad drei hinsichtlich dieser neuen Triangulierung, indem man die Funktionswerte und die beiden ersten Ableitungen in allen Eckpunkten von T, sowie die ersten orthogonalen Ableitungen in den Mittelpunkten jeder Kante von T für s(x, y) festlegt.

Bereits oben wurde angesprochen, daß im Gegensatz zu Splines in einer Variablen selbst Standardprobleme für bivariate Splines schwierig und zum Teil ungelöst sind. So wurden beispielsweise erst seit Beginn der 90er Jahre Lagrange-Interpolationspunkte für bivariate Splines konstruiert; zunächst für gleichmäßige Triangulierungen (siehe Abbildung 7) – in neuester Zeit auch für allgemeinere Klassen von Triangulierungen. An der Universität Mannheim wurden diese Interpolationsmethoden für die Konstruktion von glatten Oberflächen mit bivariaten Splines entwickelt. Abbildung 8 zeigt eine solche Splineoberfläche, welche zur Approximation eines Terrains verwendet wurde

Abschließend sie noch erwähnt, daß sich parallel zur hier geschilderten und sehr verbreiteten Theorie der reellen Splines auch eine kleine Theorie der Splinefunktionen im Komplexen entwickelt hat. Dies sind komplexwertige Funktionen komplexer Variabler, was eine z.T. von der hier geschilderten abweichende Struktur der Ergebnisse und Techniken zur Folge hat. Eine genauere Schilderung würde hier zu weit führen, es sei auf die Monographie [7] verwiesen.

Für weitere Informationen über das sich rasch entwickelnde und weite Teile der Angewandten Mathematik beeinflussende Gebiet der Splinefunktionen wird auf die angegebene Literatur verwiesen.

Literatur

[1] Collatz, L.; Quade, W.: Zur Interpolationstheorie der reellen periodischen Funktionen. Sitzungsber. Preuss. Akad. Wiss., 1938.

[2] de Boor, C.: A Pracical Guide to Splines. Springer-Verlag New York, 1978.

[3] Nürnberger, G.: Approximation by Spline Functions. Springer-Verlag Berlin/Heidelberg/New York, 1989.

[4] Nürnberger, G.; Zeilfelder, F.: Developments in Bivariate Spline Interpolation. J. Comp. Appl. Math. 121, 2000.

[5] Schoenberg, I.J.: Cardinal Spline Interpolation. CBMS 12, SIAM, Philadelphia, 1973.

[6] Schumaker, L.L.: Spline Functions: Basic Theory. John Wiley and Sons New York/Chichester, 1980.

[7] Walz, G.: Spline-Funktionen im Komplexen. B.I.-Wissenschaftsverlag Mannheim, 1991.