Lexikon der Mathematik: Stringtheorie
Ziel der Stringtheorie ist die Vereinheitlichung der Naturgesetze, denen die Elementarteilchen und die zwischen ihnen wirkenden Kräfte unterworfen sind. Drei der vier bekannten Wechselwirkungen – die elektromagnetische, die schwache und die starke Wechselwirkung – werden durch das Standardmodell der Elementarteilchenphysik im Rahmen einer Quantenfeldtheorie mit Yang-Mills-Eichgruppe U(1) × SU(2) × SU(3) erfolgreich beschrieben. Alle Versuche, eine Quantentheorie der Gravitation im Rahmen der Quantenfeldtheorie zu formulieren, stoßen jedoch auf Schwierigkeiten. Während die Unendlichkeiten (Ultraviolettdivergenzen), die bei der Berechnung physikalischer Prozesse auftreten, sich im Rahmen des Standardmodells mit Hilfe eines Renormierungsverfahrens kontrollieren lassen, ist dies nach Hinzunahme der Gravitation nicht mehr der Fall.
Die Stringtheorie weicht nun von der Vorstellung ab, daß die elementaren Bausteine der Natur punktförmige Teilchen sind, und ersetzt diese durch ein eindimensionales Objekt, den String. Die in der Natur vorkommenden Elementarteilchen sind harmonische Schwingungen dieser Strings. Es gibt eine unendliche Anzahl dieser harmonischen Schwingungen mit wachsender Masse.
Die Details des Teilchenspektrums und ihre Wechselwirkungen hängen von der jeweiligen Stringtheorie ab. Insbesondere unterscheidet man zwischen offenen und geschlossenen Strings. Ein offener String kann sich, wenn seine beiden Enden aufeinandertreffen, schließen und so zu einem geschlossenen String werden. Es gibt demnach Theorien mit offenen und geschlossenen Strings, aber auch Theorien mit nur geschlossenen Strings.
Außerdem unterscheidet man zwischen dem bo sonischen und dem fermionischen String. Die den Anregungsmoden des bosonischen Strings entsprechenden Elementarteilchen sind allesamt Bosonen, während man beim fermionischen String sowohl Bosonen als auch Fermionen erhält. Es existiert im Spektrum des geschlossenen Strings immer eine Schwingungsmode, die mit dem masselosen Graviton, das zwischen zwei gravitativ wechselwirkenden Körpern ausgetauscht wird, u. a. anhand seiner Wechselwirkungen identifiziert werden kann.
Einsteins (klassische) Allgemeine Relativitätstheorie beinhaltet die Lichtgeschwindigkeit c sowie die Newtonsche Gravitationskonstante GN als fundamentale Naturkonstanten. In einer Quantentheorie der Gravitation muß zusätzlich das Plancksche Wirkungsquantum ħ auftreten.
In der Stringtheorie wird GN durch die Stringspannung T als fundamentale Naturkonstante ersetzt und GN aus ihr bestimmt. Durch die Stringspannung werden eine für die Stringtheorie charakteristische Längenskala
und Energieskala
definiert. So ist etwa die typische Ausdehnung eines Strings durch ls bestimmt, und die Massen seiner Anregungen sind ganzzahlige Vielfache von Es/c2. ħ wird durch eine Quantisierungsvorschrift (z. B. Lichtkegelquantisierung, Pfadintegralquantisierung, BRST-Quantisierung) eingeführt.
Die klassische Gravitationstheorie, die auf der Riemannschen Geometrie beruht, verliert ihre Gültigkeit bei Distanzen
oder, dazu äquivalent, bei Energien E >Es, wo sie durch eine Quantentheorie der Gravitation ersetzt werden muß, in der die klassischen Konzepte von Raum und Zeit modifiziert werden müssen.
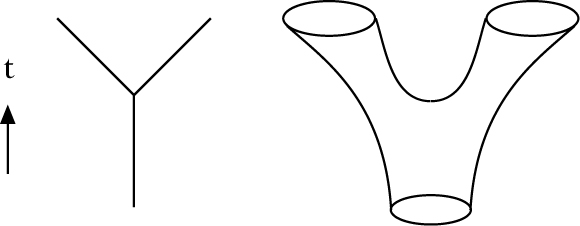
Der Übergang von nulldimensionalen zu eindimensionalen Grundbausteinen hat weitreichende Konsequenzen, die man heuristisch wie folgt einsehen kann. Während die Raum-Zeit-Trajektorien von Punktteilchen Weltlinien sind, sind diejenigen von Strings zweidimensionale Weltflächen. Die Weltfläche eines frei propagierenden offenen Strings hat die Topologie eines Streifens, die eines geschlossenen Strings die eines Zylinders. Die Weltflächen wechselwirkender Strings haben eine kompliziertere Topologie. Vergleicht man nun z. B. die Raum-Zeit-Trajektorien eines zerfallenden Teilchens mit der eines zerfallenden Strings, so sieht man, daß, während die Weltlinie im Falle des Teilchens einen singulären Verzweigungspunkt hat, die Wechselwirkung im Falle des Strings verschmiert ist.
Weltlinie eines zerfallenden Teilchens und Weltfläche eines zerfallenden geschlossenen Strings.
Das hat zur Folge, daß die Divergenzen, die eine quantenfeldtheoretische Formulierung der Gravitation allem Anschein nach unmöglich machen, nicht mehr auftreten. Dadurch, daß alle verschiedenen Elementarteilchen durch ein fundamentales Objekt beschrieben werden, erreicht man auch die gewünschte Vereinheitlichung, bei der die Gravitation notwendigerweise mit eingeschlossen ist.
Die Quantisierung des Strings ist bisher nur in einem vorgegebenen, klassischen Raum-Zeit-Hintergrund möglich. Am einfachsten ist die Quantisierung des freien Strings in einer Minkowskischen Raum-Zeit. Wie auch bei Punktteilchentheorien ist dabei zu beachten, daß sich ein positiv definiter Hilbertraum ergibt, und die Symmetrien der klassischen Theorie (Raum-Zeit-Symmetrien, Eichsymmetrien, Reparametrisierungs- und Skaleninvarianz auf der Weltfläche) erhalten bleiben (Anomaliefreiheit). Diese Forderungen bedeuten starke Einschränkungen an die möglichen konsistenten Stringtheorien. Eine wichtige Einschränkung ist die, daß sich die Stringtheorie nicht im Minkowsi-Raum von beliebiger Dimension quantisieren läßt, sondern nur in der sogenannten kritischen Dimension, die für den bosonischen String dkrit = 26, und für den fermionischen String dkrit = 10 ist. Neben endlich vielen masselosen und unendlich vielen massiven Anregungen enthält das Spektrum des bosonischen Strings immer ein Tachyon ((Masse)2< 0), das eine Instabilität signalisiert. Der fermionische String kann dagegen durch eine zusätzliche Projektion (GSO-Projektion) so eingeschränkt werden, daß ein tachyonfreies, supersymmetrisches Spektrum resultiert. Gleichzeitig wird erreicht, daß keine Anomalien auftreten (modulare Invarianz).
Supersymmetrie ist eine Symmetrie zwischen Fermionen und Bosonen. Sie stellt eine Erweiterung der Raum-Zeit-Symmetrien dar: Zusätzlich zu den Symmetriegeneratoren der Poincaré-Algebra (Translationen, Rotationen und Lorentztransformationen) gibt es \({\mathcal{N}}\) fermionische Generatoren, die man als Superladungen bezeichnet. Yang-Mills Eichtheorien sowie die Allgemeine Relativitätstheorie erlauben, unter Hinzunahme von weiteren fermionischen und bosonischen Feldern (Superpartner der Eichfelder bzw. der Metrik), Erweiterungen, die invariant unter Supersymmetrietransformationen sind. Diese supersymmetrischen Feldtheorien bezeichnet man als Super-Yang-Mills– bzw. Supergravitationstheorie. Supersymmetrische Yang-Mills-Theorien existieren in d ≤ 10 Dimensionen, Supergravitationstheorien in d ≤ 11. In der Stringtheorie kann Supersymmetrie in der Raum-Zeit auf eine Supersymmetrie auf der zweidimensionalen Weltfläche zurückgeführt werden.
In einer Theorie mit nur geschlossenen Strings besitzt das Spektrum \({\mathcal{N}}\) = 2 Supersymmetrie in zehn Dimensionen. Zwei inäquivalente GSO-Projektionen führen zu der nichtchiralen (linksrechts symmetrischen) Typ IIA und der chiralen (linksrechts asymmetrischen) Typ IIB Theorie. Ihre masselosen Spektren sind die der zehndimensionalen Typ IIA bzw. Typ IIB Supergravitationstheorien. Das Spektrum der Typ I Theorie mit offenen und geschlossenen Strings ist \({\mathcal{N}}\) = 1 supersymmetrisch und enthält im masselosen Sektor supersymmetrische Yang-Mills Theorie, gekoppelt an Supergravitation. Die Freiheitsgrade der Yang-Mills Theorie sind im Anregungsspektrum des offenen Strings. Das Graviton und seine supersymmetrischen Partner sind wie in den Typ II Theorien im masselosen Anregungsspektrum des geschlossenen Strings. Die Konsistenz der Typ I Theorie fordert, daß die Eichgruppe die orthogonale Gruppe SO(32) ist – nur dann verschwinden alle Eich- und Gravitationsanomalien.
Die Typ I und Typ II Theorien werden auch als Superstringtheorien bezeichnet. Neben der Typ I Theorie gibt es zwei weitere Stringtheorien mit \({\mathcal{N}}\) = 1 Raum-Zeit-Supersymmetrie, den heterotischen E8 × E8 sowie den heterotischen SO(32) String. Diese beiden Stringtheorien haben, wie die Typ II Theorien, nur geschlossene Strings, aber eine andere Weltflächensupersymmetrie. Die Einschränkung auf nur zwei mögliche Eichgruppen ist eine Konsequenz der modularen Invarianz. Das masselose Spektrum der heterotischen Stringtheorien ist wiederum dasjenige einer supersymmetrischen Yang-Mills-Theorie, gekoppelt an Supergravitation – diesmal mit Eichgruppe E8 × E8 oder SO(32). Die fünf supersymmetrischen Stringtheorien (Typ I, IIA, IIB, und die beiden heterotischen Theorien) sind die einzigen bekannten Stringtheorien, die alle Konsistenzkriterien erfüllen.
Der störungstheoretischen Berechnung von Streuamplituden durch Summation über Feynman-Diagramme entspricht in der Stringtheorie die Summation über Weltflächen unterschiedlicher Topologie. Die erlaubten Topologien hängen dabei vom betrachteten Prozeß und der jeweiligen Stringtheorie ab. Nicht-orientierbare Weltflächen kommen nur in der Typ I Theorie vor.
Die Stärke der Wechselwirkung wird durch die Stringkopplungskonstante g kontrolliert. g ist durch den Wert eines skalaren Feldes, des Dilatons, das neben dem Graviton als einziges Feld zum masselosen Spektrum jeder Stringtheorie gehört, bestimmt. Die Kopplungskonstanten der verschiedenen Stringtheorien sind a priori voneinander unabhängig. Die Potenz von g, zu der eine Weltfläche in der Störungsreihe beiträgt, ist durch ihre Eulerzahl bestimmt. Die Gültigkeit der Störungsreihe setzt dabei, wie auch in der Quantenfeldtheorie, g ≪ 1 voraus.
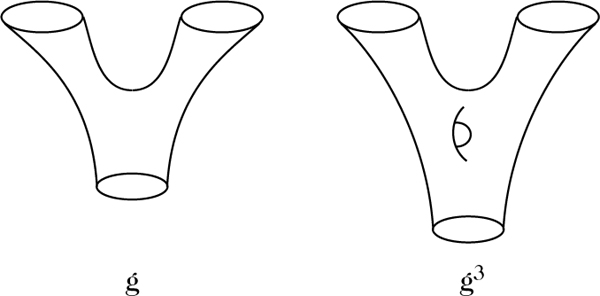
Beiträge zum Zerfall eines geschlossenen Strings in zwei geschlossene Strings in den Ordnungen g und g3.
Für Energien E ≪ Es stimmen die Streuamplituden, die z. B. im Rahmen der konformen Feldtheorie als Korrelationsfunktionen von Vertexoperatoren berechnet werden können, mit denen einer effektiven Feldtheorie überein, die für jede der fünf Stringtheorien gerade die jeweilige supersymmetrische Feldtheorie ist.
Für Energien E >Es wird die endliche Ausdehnung des Strings relevant, und Abweichungen von Quantenfeldtheorien werden bemerkbar, was sich u. a. in der schon erwähnten Endlichkeit von Streuamplituden niederschlägt. Im Rahmen der Stringtheorie können nun z. B. Quantenkorrekturen zur Gravitationswechselwirkung berechnet werden.
Soll die Stringtheorie eine physikalische Theorie sein, muß es möglich sein, sie in einer (topologisch und metrisch nichttrivialen) Raum-Zeit zu formulieren, in der nur d = 4 Dimensionen von unendlicher, die verbleibenden dint = dcrit − d Dimensionen aber von endlicher Ausdehnung sind. Eine mögliche Realisierung einer solchen Kompaktifizierung beginnt mit dem Faktorisierungsansatz Md × Kint für die zehndimensionale Raumzeit. Hier ist Md der d-dimensionale Minkowski-Raum und Kint ein dint -dimensionaler kompakter Raum. Allgemein wird eine Kompaktifizierung durch Kint, eine Riemannsche Metrik auf Kint, und die Werte weiterer Tensorfelder, die sich im masselosen Teil des Spektrums der jeweiligen Stringtheorie befinden, spezifiziert. Die notwendige Forderung nach Skaleninvarianz auf der Weltfläche schränkt die möglichen Kompaktifizierungen ein. Die resultierende d-dimensionale Theorie hängt stark von der Wahl der Kompaktifizierung ab. Beispielsweise erhält man eine d-dimensionale supersymmetrische Theorie nur für solche Kint, auf denen Killingspinoren existieren.
Bei der Kompaktifizierung führt die Tatsache, daß Strings eindimensional sind, zu interessanten Symmetrien. Das Massenspektrum von Teilchen, die sich auf einer Riemannschen Mannigfaltigkeit bewegen, ist durch die Eigenwerte des Laplace-Operators bestimmt. Geometrisch und topologisch unterschiedliche Mannigfaltigkeiten führen in der Regel zu verschiedenen Spektren. Für einen Kreis mit Radius R findet man die Kaluza-Klein-Anregungen mit
Für R → ∞ ergibt sich ein Kontinuum, welches ein Signal für eine unendlich ausgedehnte Richtung ist. Das Spektrum eines geschlossenen Strings auf einem Kreis ist dagegen ganz anders geartet, da sich der String nicht nur auf dem Kreis bewegen, sondern sich auch um ihn wickeln kann. Das kostet Energie, die sowohl von der Windungszahl w als auch vom Radius des Kreises abhängt, da der String gegen seine Spannung T gedehnt werden muß. Man findet jetzt die erlaubten Werte
Dieses Spektrum ist symmetrisch unter der diskreten T-Dualitätstransformation \(R\to {l}_{s}^{2}/R\), bei der Kaluza-Klein-Anregungen und Windungszustände ihre Rollen vertauschen. Die Symmetrie gilt auch für die Streuamplituden des bosonischen Strings, wenn man zusätzlich g → gls/R transformiert. Es entsprechen also geometrisch unterschiedliche Kompaktifizierungen physikalisch identischen Theorien. Sowohl für R → ∞ als auch für R → 0 erhält man ein Kontinuum von masselosen Zuständen, was man als die Dekompaktifizierung einer zusätzlichen Dimension interpretiert. Für Typ II Theorien transformiert die T-Dualität die Typ IIA Theorie auf \({S}_{R}^{1}\) in die Typ IIB Theorie auf \({S}_{{l}_{s}^{2}/R}^{1}\).
Allgemein bezeichnet man diskrete Symmetrien zwischen den Kompaktifizierungen auf zwei geometrisch und in vielen Fällen auch topologisch verschiedenen Mannigfaltigkeiten \({K}_{1}^{\mathrm{int}}\) und \({K}_{1}^{\mathrm{int}}\), die zu physikalisch identischen d-dimensionalen Stringtheorien führen und exakt in jeder Ordnung in g sind, als T-Dualität. Die mirrorsymmetry der Kompaktifizierung auf Calabi-Yau-Mannigfaltigkeiten ist ein interessantes Beispiel einer T-Dualität. Sie tritt bei den physikalisch interessanten Kompaktifizierungen des heterotischen Strings auf sechsdimensionalen Calabi-Yau-Mannigfaltigkeiten auf, die vierdimensionale Stringtheorien mit \({\mathcal{N}}\) = 1 Supersymmetrie ergeben. Zu jeder CY-Mannigfaltigkeit K1 existiert nun immer eine Spiegel-CY-Mannigfaltigkeit K2 so, daß die Kompaktifizierungen auf K1 und K2 zu identischen vierdimensionalen Stringtheorien führen. Hierbei haben K1 und K2 verschiedene Topologie. Im Falle der Kompaktifizierung des Typ II Strings auf CY-Mannigfaltigkeiten gilt
Wie die T-Dualität zeigt, ist für Strings, im Gegensatz zu Punktteilchen, nicht die klassische Geometrie oder gar Topologie der Raum-Zeit relevant, sondern vielmehr eine ‘Stringgeometrie’. Diese Modifikation der Raum-Zeit-Geometrie wird bei Längenskalen l ≤ ls wichtig, und es besteht die Hoffnung, daß die Stringtheorie zu Einsichten über die Physik bei diesen kleinen Distanzen führt. Insbesondere sollte in einer vollständigen Theorie der Quantengravitation die bisher als fest vorgegebene Raum-Zeit-Geometrie, durch die sich der String bewegt, dynamisch erzeugt werden. Diesen Anspruch kann die Stringtheorie bisher nicht erfüllen, u. a. auch wegen ihrer bislang ausschließlich störungstheoretischen Formulierung, die allen vorangegangenen Betrachtungen zugrunde lag. Die Formulierung der Stringtheorie, die zu dieser Störungsreihe führt, fehlt noch.
Einen Zugang zu nichtstörungstheoretischer Information eröffnet die aus supersymmetrischen Quantenfeldtheorien bekannte Dualität zwischen stark (g ≫ 1) und schwach (g ≪ 1) gekoppelten Theorien. Sie ermöglicht es, die Theorie bei starker Kopplung mit perturbativen Methoden in der dualen, schwach gekoppelten Theorie zu kontrollieren. Die zueinander dualen Theorien können störungstheoretisch sehr unterschiedlich sein und sich z. B. in ihren Freiheitsgraden und Symmetrien voneinander unterscheiden. So können die in der Störungstheorie relevanten Freiheitsgrade der einen Theorie Solitonen, also lokalisierte Lösungen der klassischen Bewegungsgleichungen, der (schwachgekoppelten) dualen Theorie sein. Diese gehören zum nichtperturbativen Spektrum, da ihre Massen für g → 0 divergieren und die Zustände somit entkoppeln. Falls die Solitonen bei starker Kopplung, d. h. g → ∞, sehr leicht werden und schwach gekoppelt sind, übernehmen sie in der dualen Theorie die Rolle der elementaren Anregungen. Die Dualität zwischen stark und schwach gekoppelten Theorien bezeichnet man als S-Dualität, wenn sie in jeder Ordnung in E/Es gilt. Von U-Dualität spricht man, wenn diskrete Symmetrien vorliegen, die die Ordnungen sowohl in g als auch in E/Es mischen.
Der Beweis der S-Dualität (oder U-Dualität) ist schwierig ohne eine nichtstörungstheoretische Formulierung der Theorie. Man kann aber die Dualitätshypothese an solchen solitonischen Zuständen überprüfen, deren Quantenkorrekturen unter Kontrolle sind, und deren Massen als Funktionen von g bei schwacher Kopplung vollständig bestimmt werden können. Extrapolation in den Bereich starker Kopplung ist dann zulässig, und ein Vergleich mit den störungstheoretischen Zuständen der dualen Theorie möglich. Solche Zustände existieren in Feld- bzw. Stringtheorien mit \({\mathcal{N}}\) > 1 Supersymmetrie und werden als BPS-Zustände bezeichnet.
Zum BPS-Spektrum der Stringtheorie gehören insbesondere sogenannte Branen. Man findet sie als stabile klassische Lösungen der Supergravitationstheorien, die ausgedehnte Objekte beschreiben: Teilchen (0-Brane), Strings (1-Brane), Membranen (2-Brane), oder allgemein p-Branen. Welcher dieser Lösungen vorkommen, hängt von der gewählten Supergravitationstheorie ab. Offene Strings werden durch ihre Randbedingungen in jeder Richtung im Raum charakterisiert. Die üblicherweise gestellten Neumall-Randbedingungen bedeuten physikalisch, daß an den Enden des offenen Strings kein Impuls abfließt. Unterwirft man jedoch ein Ende des offenen Strings in (9 − p) der Raumrichtungen Dirichlet-Randbedingungen, so findet man, daß nun Impuls über dieses Ende abfließen kann, der aufgrund der Impulserhaltung auf neue (dynamische) p-dimensionale Objekte, die D(irichlet)p-Branen, übertragen werden muß.
Detaillierte Betrachtungen ergeben, daß es sich bei diesen beiden Beschreibungen der Branen um dasselbe Objekt handelt. Ihre Massendichte divergiert bei verschwindender Stringkopplung g, und deshalb sind sie im perturbativen Spektrum der Theorie nicht sichtbar. Bei starker Kopplung werden sie jedoch sehr leicht und können in manchen Fällen als die fundamentalen Objekte einer dualen Theorie mit Kopplung 1/g interpretiert werden.
Ein Beispiel in d = 10 ist die S-Dualität zwischen dem heterotischen SO(32)-String und dem Typ I-String. Es gilt gI = 1/ghet, und die D1-Brane der Typ I Theorie wird im Limes starker Typ I Kopplung auf den fundamentalen heterotischen String abgebildet.
Die Typ IIA Theorie besitzt BPS-Zustände von n D0-Branen mit Masse
Diese Zustände können als Kaluza-Klein-Anregungen einer auf S1 kompaktifizierten Theorie mit Radius R11 = gIIAls interpretiert werden. Im Limes gIIA → ∞, also bei starker Kopplung, resultiert aus der zehndimensionalen Typ IIA Theorie eine Theorie in elf Dimensionen! Ihre masselosen Freiheitsgrade und Wechselwirkungen werden bei niedrigen Energien durch die elfdimensionale Supergravitation mit charakteristischer Energieskala \({E}_{SG}={g}_{\text{IIA}}^{-1/3}{E}_{s}\) beschrieben.
Bei Energien O(ESG) liefert weder die Stringtheorie noch die Supergravitation eine adäquate Beschreibung. Der noch unbekannten Theorie, die dies leistet, hat man den Namen M-Theorie gegeben. Auch der stark gekoppelte E8 ×E8 heterotische String kann als Kompaktifizierung – diesmal auf einem Intervall der Länge R11 – dieser M-Theorie interpretiert werden. Je ein E8 Faktor ist auf einem der beiden zehndimensionalen Ränder lokalisiert.
Diese und viele andere Dualitätsrelationen implizieren, daß alle fünf Stringtheorien lediglich verschiedene störungstheoretische Approximationen ein und derselben fundamentalen Theorie sind. Das Auftreten der elfdimensionalen Supergravitation bedeutet, daß die Stringtheorie keine komplette Beschreibung im Bereich starker Kopplung liefern kann. Die hypothetische Theorie, aus der sich sowohl die Stringtheorien als auch die elfdimensionale Supergravitationstheorie in verschiedenen Näherungen ableiten lassen, ist die schon erwähnte M-Theorie. Die elementaren Anregungen dieser Theorie hängen von der gewählten Approximation ab. Ihre BPS-Zustände sind die sogenannten M2- und M5-Branen, die bisher nur als klassische Lösungen der Supergravitationstheorie konstruiert werden können. Dann läßt sich z. B. der Typ IIA String als eine M2-Brane, deren eine Dimensionen um den Kreis mit Radius R11 gewickelt ist, interpretieren
Zum gegenwärtigen Zeitpunkt ist die Stringtheorie noch keine abgeschlossene physikalische Theorie, insbesondere eine über die Störungstheorie hinausgehende Formulierung fehlt noch. Von einer solchen Formulierung erhofft man sich auch, daß die freien Parameter der Kompaktifizierung, die den Werten der masselosen Felder entsprechen (Metrik, Dilaton, etc.), und die Parameter der effektiven Feldtheorie (z. B. Eich-, Yukawakopplungen), dynamisch bestimmt werden.
Da die charakteristische Energie E2 ∼ MPlanckc2 um viele Gößenordnungen über den experimentell erreichbaren Energien liegt, ist die direkte Verifizierung der Stringtheorie sehr schwierig. Andererseits wird jede Quantentheorie der Gravitation mit diesem Problem zu kämpfen haben. Unter den existierenden Ansätzen für eine solche Theorie ist die Stringtheorie z.Zt. die vielversprechendste.
Literatur
[1] Green, M.; Schwarz, J.; Witten, E.: Superstring Theory, Vol. I+II. Cambridge University Press, 1987.
[2] Lüst, D.; Theisen, S.: Lectures on String Theory. Springer Verlag, 1989.
[3] Polchinski, J.: String Theory, Vol. I+II. Cambridge University Press, 1998.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.