Lexikon der Mathematik: surreale Zahlen
Conway-Zahlen, von John Horton Conway ab dem Jahr 1970 untersuchter und 1976 in seinem Buch „On Numbers and Games“ (ONAG), dessen Originalausgabe seit dem Jahr 2001 in einer Neubearbeitung [3] vorliegt, beschriebener reell-abgeschlossener nichtarchimedischer Körper No. Die Bezeichnung surreale Zahlen ist von Donald Ervin Knuth geprägt worden, der Conways Zahlen schon 1974 im Rahmen einer Novelle kurz vorstellt hatte [6]. Conway selbst nennt die Elemente von No einfach nur Zahlen, weil No die reellen Zahlen und auch die Ordinalzahlen umfaßt. Insbesondere ist No keine Menge, sondern eine echte Klasse.
Conway definiert die Zahlen auf eine rekursive Weise als Paare aus einer linken und einer rechten Menge von Zahlen, die eine gewisse Schnittbedingung (keine Zahl der linken Menge ist größer als eine Zahl der rechten Menge) erfüllen. Diese Conway-Schnitte lassen sich als eine Verallgemeinerung der (ausgehend von den rationalen Zahlen) zur Einführung der reellen Zahlen benutzten Dedekind-Schnitte sehen. Während jedoch die Dedekind-Schnittbildung ein einschrittiger Vorgang mit dem Ziel des Ausfüllens der ‚Lücken‘ zwischen den rationalen Zahlen und damit der Vervollständigung des Körpers ℚ ist, dessen Wiederholung nichts Zusätzliches bringt, werden bei der wiederholten Conway-Schnittbildung immer neue Lücken zwischen den bereits erzeugten Zahlen aufgerissen und mit neugebildeten Zahlen gefüllt, und dies nicht nur bei endlicher, sondern auch bei transfiniter Wiederholung, wobei auch unendlich kleine und unendlich große Zahlen entstehen. Man kann jeder Zahl eine Ordinalzahl als Geburtstag zuordnen, sozusagen der ‚Zeitpunkt‘ ihrer Erzeugung in diesem transfiniten Prozeß. Die Rekursion beginnt bei der Zahl Null als einem Paar leerer Mengen. So entstehen also Conways Zahlen gewissermaßen aus dem Nichts, ähnlich wie die nichtnegativen ganzen Zahlen oder allgemeiner die Ordinalzahlen gemäß John von Neumanns Konstruktion, wo jede Ordinalzahl gerade als die Menge aller kleineren Ordinalzahlen definiert ist, beginnend mit 0 := ∅, 1 := {0}, 2 := {0, 1}, …, ω := {0, 1, 2, …}, ω + 1 := {0, 1, 2, …, ω}, … und allgemein α = {β | β< α}. Während jedoch bei von Neumann eine Ordinalzahl die Menge all ihrer Vorgänger ist, ist bei Conway eine Zahl ein Paar von Mengen von Vorgängern.
Conway gelangte durch die Untersuchung von Spielen zu seiner Definition der Zahlen. Es ist möglich und zweckmäßig, zunächst Spiele einzuführen und dann die Zahlen als spezielle Spiele.
Da die Zahlen, ihre Ordnung und ihre Operationen rekursiv definiert sind, lassen sich Aussagen über sie oft am bequemsten induktiv beweisen, wobei für den Induktionsanfang i. d. R. gar nichts gezeigt werden muß, weil er eine Aussage über Elemente der leeren Menge ist.
Man kann die Zahlen in einer Baumstruktur ordinaler Höhe anordnen, an deren Wurzel die am nullten Tag erzeugte Null steht und in jeder Ebene, der Größe nach geordnet, die am zugehörigen Tag α neu erzeugten Zahlen. Gemäß Philip Ehrlich [4] läßt sich No auch als vollständige binäre Baumstruktur definieren, in der jedes Element x ein Mengenpaar (Lx, Rx) dergestalt ist, daß Lx alle linken Vorgänger und Rx alle rechten Vorgänger von x enthält.
Jede Zahl läßt sich in einer Normalform darstellen, die sich mit einer ordinalen Vorzeichenfolge (d. h. einer Abbildung von den Ordinalzahlen in eine Menge {−, 0, +}) identifizieren läßt. Die Ordnung der Zahlen entspricht der lexikographischen Ordnung der Vorzeichenfolgen. Umgekehrt definiert z. B. Harry Gonshor [5] die Zahlen als derartige Vorzeichenfolgen, auch um Conways zunächst etwas ungewohnte halbformale Herangehensweise durch einen strengen formalen Zugang zu ersetzen. Weitere Vorteile dieser Methode sind, daß man sich auf ‚vertrautem Gelände‘ (Ordinalzahlen) bewegt, und daß die Begriffe Gleichheit und Identität von Zahlen zusammenfallen, während bei Conway die Gleichheit von Zahlen eine definierte Äquivalenzrelation ist und sich von der Identität unterscheidet. Leider gibt es für allgemeine Spiele keine der Vorzeichenentwicklung von Zahlen entsprechende Darstellung. Ferner müssen bei diesem Zugang die Ordinalzahlen schon bekannt sein, während sie bei Conways Methode auf natürliche Weise miterzeugt werden. Conway merkt auch an, daß bei der Definition über Vorzeichenfolgen eine Zahl ein recht kompliziertes Ding ist.
Zur Erläuterung nun eine kurze Darstellung des ‚rekursiven Zugangs‘ zu den Zahlen. Dabei ist {L | R} eine chreibweise für ein Paar (L, R) von Mengen L und R. Man nennt L linke Menge, R rechte Menge, Elemente von L linke Optionen und Elemente von R rechte Optionen von {L | R}. Sind a, b, c, … und u, v, w, … Elemente, so schreibt man unter Weglassung der Mengenklammern auch {a, b, c, … | u, v, w, …} anstelle von {{a, b, c, …} | {u, v, w, …}}.
Für ein solches x = {L | R} bezeichnet xL ein typisches (d. h. irgendein) Element von L und xR ein typisches Element von R, und man schreibt damit auch x = {xL | xR}. Schreibt man eine Aussage für xL bzw. xR, so soll dies bedeuten, daß sie für alle linken bzw. rechten Optionen von x gilt, und entsprechend auch für Aussagen in mehreren Variablen.
Zahlen als Conway-Schnitte
Mit diesen Bezeichnungen lassen sich die Zahlen zusammen mit der Relation ≥ durch nur zwei Regeln definieren:
- Sind L, R Mengen von Zahlen, und gilt xL ≱ xR für x := {L | R}, dann ist x eine Zahl. Alle Zahlen entstehen auf diese Weise.
- Für zwei Zahlen x und y schreibt man x ≥ y genau dann, wenn y ≱ xR und yL ≱ x gilt.
Ein Ausdruck x = {L | R} mit Zahlenmengen L, R mit xL ≱ xR heißt nach Norman L. Alling [1] auch Conway-Schnitt. Zahlen sind also definiert als Conway-Schnitte in den Zahlen. Hierzu einige Anmerkungen:
- Auf den ersten Blick erscheint die Definition zyklisch: Um zu erklären, was eine Zahl ist, braucht man schon die Relation ≥ für Zahlen. Die Klasse No aller Zahlen ist hiermit aber doch wohldefiniert, weil immer nur Bezug auf die Optionen einer Zahl genommen wird. Durch die Vorschrift „Alle Zahlen entstehen auf diese Weise“ und das Fundierungsaxiom der Mengenlehre wird gewährleistet, daß die Rekursion, egal von welcher Zahl man ausgeht, letztlich bei der leeren Menge endet, daß Relationen und insbesondere Funktionen von Zahlen sich rekursiv definieren und geeignete Aussagen über Zahlen sich induktiven beweisen lassen. Ist etwa P(x) eine Aussageform für Zahlen, und folgt aus der Gültigkeit von P(xL) und P(xR) die Gültigkeit von P(x), dann gilt P(x) für alle Zahlen x. Eine anschaulichere Sichtweise ist, die beiden Regeln nicht als Axiome aufzufassen, sondern als Konstruktionsregeln, und sich vorzustellen, daß die Zahlen, beginnend mit {|}, schrittweise der Reihe nach ‚erzeugt‘ werden.
- Ein Conway-Schnitt unterscheidet sich von einem Dedekind-Schnitt im wesentlichen dadurch, daß linke und rechte Menge leer sein dürfen, und dadurch, daß es keine Einschränkung der Art „R hat kein kleinstes Element“ gibt. Der erste Unterschied bewirkt die Existenz unendlich großer Zahlen, während der zweite dafür sorgt, daß immer wieder zusätzliche Zahlen zwischen die schon vorhandenen Zahlen eingeschoben werden können. Dedekind wollte von ℚ zu ℝ kommen und mußte daher an seine Schnitte stärkere Forderungen stellen.
- Werden in einem bestimmten Schritt der Zahlengenese aus den schon erzeugten Zahlen alle nach den Regeln erlaubten neuen Zahlen gebildet, so werden alle schon vorhandenen Zahlen wieder miterzeugt, denn alle ihre Optionen sind ja auch Zahlen und stehen zur Schnittbildung zur Verfügung.
- Der Grund, nicht xL< xR zu fordern anstelle von xL ≱ xR, obwohl dies gemäß nachfolgender Definition äquivalent wäre, wird weiter unten beim Zugang über Spiele deutlich.
Die Relationen ≤, =, > und < sind für Zahlen x und y wie folgt definiert:
Bemerkenswert ist, daß die Gleichheit von Zahlen eine definierte Äquivalenzrelation ist. Man muß daher etwa die trivial erscheinende Formel x = x für Zahlen x beweisen. Ferner können zwei verschiedene Conway-Schnitte die gleiche Zahl bezeichnen. Eine naheliegendes Vorgehen wäre es daher, Zahlen als Äquivalenzklassen von Schnitten zu definieren und dann z. B. auch nicht von ‚der‘ linken Menge einer Zahl zu reden, sondern nur von der linken Menge eines die Zahl darstellenden Schnitts. Dagegen spricht u. a., daß diese Äquivalenzklassen i. a. echte Klassen wären.
Addition und Multiplikation von Zahlen x, y sind rekursiv definiert:
Diese Definitionen sind verträglich mit der Gleichheitsrelation: Für alle Zahlen x1, x2, y1, y2 mit x1 = x2 und y1 = y2 hat man x1 + y1 = x2 + y2 und x1y1 = x2y2.
Man kann nun nachrechnen, daß auf diese Weise ein geordneter Körper No definiert wird, dessen Nullelement die bei der Wahl von linker und rechter Menge als leere Menge entstehende erste und einfachste Zahl 0 := {|} und dessen Einselement die Zahl 1 := {0 |} ist. Das Negative einer Zahl x ist einfach −x = {−xR | − xL} während das Reziproke einer surrealen Zahl eine etwas aufwendigere Gestalt hat.
Zahlen als Spiele
Beim Zugang zu den Zahlen über Spiele führt man zunächst diese ein und dann die Zahlen als diejenigen Spiele x, deren Optionen allesamt Zahlen sind mit xL ≱ xR. Die Relationen ≥, ≤, =, >, < und die Addition und Multiplikation sind dann also schon als die entsprechenden Relationen und Operationen der Spiele gegeben. Die Spiele 0 und 1 sind Zahlen, und Summen, Negative und Produkte von Spielen, die Zahlen sind, sind wieder Zahlen. Zu jeder von Null verschiedenen Zahl gibt es eine reziproke Zahl.
Während die Spiele nur halbgeordnet sind, ist die Ordnung auf den Zahlen total, und während die arithmetischen Operationen der Spiele nicht notwendig mit deren Gleichheitsrelation verträglich sind (es gibt Spiele x und y = z mit xy ≠ xz), ist dies für Zahlen der Fall. Die Spiele 0 und 1 sind Zahlen, und man erhält den Körper No als Teilklasse der Klasse der Spiele.
Hierbei wird auch verständlich, weshalb beim obigen direkten Zugang die Gültigkeit von xL ≱ xR gefordert wurde und nicht die von xL< xR : Für die nur halbgeordneten Spiele sind diese Aussagen nicht äquivalent.
Der Einfachheitssatz
Für jede Zahl x gilt xL ≱ x ≱ xR, d. h. x liegt zwischen allen xL und xR. Der Einfachheitssatz lautet:
Ist x eine Zahl, und gilt xL ≱ z ≱ xR für eine Zahl z, aber für keine Option von z anstelle von z, dann gilt x = z.
Der Einfachheitssatz gilt auch dann, wenn man x nur als Spiel voraussetzt. Er ist ein wichtiges Hilfsmittel, um Zahlen auszuwerten oder Schnittdarstellungen zu vereinfachen. Mit ihm sieht man z. B. sofort, daß für jede Zahl x
gilt für alle Zahlen ℓ ≤ x, wobei \({x}_{\gt \ell}^{L}\) die linken Optionen von x bezeichnet, die größer als ℓ sind, und entsprechend
für alle Zahlen r ≥ x, wobei \({x}_{\lt r}^{R}\) die rechten Optionen von x bezeichnet, die kleiner als r sind, und schließlich
für alle Zahlen ℓ, r mit ℓ ≤ x ≤ r. Daher gilt etwa
für jede Zahl x > 0, was bei der Darstellung des Reziproken einer surrealen Zahl benutzt wird.
Ordinalzahlen
Ordinalzahlen sind definiert als Zahlen der Gestalt {L |}, also als Schnitte mit leerer rechter Menge. Zu jeder Menge S von Ordinalzahlen gibt es eine Ordinalzahl, die größer als jedes Element von S ist, nämlich etwa {S |}.
On bezeichnet die Klasse der Ordinalzahlen, und griechische Buchstaben stehen im folgenden immer für Elemente von On. Für jede Zahl x ist die Klasse {β< x} eine Menge. Mit dem Einfachheitssatz folgt daraus, daß α = {β< α |} gilt für alle α ∈ On und daß jede nichtleere Klasse C ⊂ On ein kleinstes Element enthält, nämlich etwa {L |} mit L als Menge aller Ordinalzahlen, die kleiner sind als alle Elemente von C. Folglich ist On wohlgeordnet. Hiermit kann man zeigen, daß On mit den sonst üblicherweise in der Mengenlehre definierten Ordinalzahlen übereinstimmt. Summe und Produkt in On entsprechen der sog. maximalen Summe und dem maximalen Produkt der üblichen Ordinalzahlarithmetik.
Geburtstage
Für jedes α ∈ On wird die Menge Mα („made numbers“) aller bis zum Tag α geborenen Zahlen definiert als die Menge aller Zahlen x, deren Optionen alle an einem früheren Tag geboren wurden, also an einem Tag Mβ mit β< α. Damit ist
(„old numbers“) die Menge der vor, und
(„new numbers“) die Menge der am Tag α geborenen Zahlen. Jedes x ∈ Nα definiert durch
einen Schnitt {L | R} in Oα, und nach dem Einfachheitssatz gilt x = {L | R}. In diesem Sinn ist Mα gerade die Vereinigung von Oα mit allen Schnitten in Oα.
Jede Zahl x liegt in genau einer Menge Nα. Die Ordinalzahl βx := α heißt Geburtstag von x. Für zwei Zahlen x, y heißt x einfacher als y, wenn βx< βy gilt. Da On wohlgeordnet ist, existiert in jeder gegebenen nicht-leeren Teilklasse von On (mindestens) ein einfachstes Element. Aus dem Einfachheitssatz ergibt sich, daß jede Zahl x die einfachste Zahl ist, die zwischen allen xL und xR liegt.
Vorzeichenentwicklungen
Zu jedem x ∈ Nα wird für jedes β< α durch
ein Schnitt {L | R} in Oβ definiert und damit ein
bezeichnet als β-te Näherung zu x. Für β ≥ α setzt man xβ := x. Durch
für jedes β ∈ On wird dann jeder Zahl x eine Vorzeichenentwicklung s(x) := (sβ)β∈On zugeordnet mit sβ ∈{−, +} für β< βx und sβ = 0 für β ≥ βx. Versieht man die Klasse der Vorzeichenfolgen, also der Funktionen s : On →{−, 0, +}, mit der lexikographischen Ordnung, so ist x ↦ s(x) eine bijektive ordnungserhaltende Abbildung von der Klasse der Zahlen auf die Klasse der Vorzeichenfolgen, die sich also identifizieren lassen. Die Vorzeichenentwicklung von −x erhält man aus der von x durch Vertauschen der Zeichen − und +. Beim Niederschreiben von Vorzeichenentwicklungen läßt man das aus lauter Nullen bestehende Endstück weg und beschränkt sich auf den aus den Zeichen − und + bestehenden Teil, also z. B. (+ + − −) anstelle von (+ + − − 000 …). So ist etwa 0 = () und 1 = (+). Neben den Zeichen − und + sind auch die Zeichen ↓ und ↑ gebräuchlich.
Eine kurze Geschichte der Zahlen
Am Anfang gibt es keine Zahlen, so daß sich als Schnitt nur die Zahl Null als
bilden läßt. Die Null ist eine Ordinalzahl und die einzige am Tag 0, dem nullten Tag, geborene Zahl.
Am nächsten Tag kann man auch die Null zur Konstruktion benutzen und kommt zu den Möglichkeiten {|}, {0|}, {|0} und {0|0}. Die Null {|} entsteht dabei nochmals, das Spiel {0|0} ist keine Zahl, aber die Schnitte
liefern neue Zahlen, wobei −1 tatsächlich das Negative von 1 ist. Die Zahl 1 ist eine Ordinalzahl. Am Tag 1, dem ersten Tag, entstehen also die neuen Zahlen −1, 1.
Auf die gleiche Weise entstehen am Tag 2, dem zweiten Tag, die neuen Zahlen
und ihre Negativen und am Tag 3, dem dritten Tag, die neuen Zahlen
und ihre Negativen. So fortgesetzt, erhält man an den endlichen Tagen alle dyadischen rationalen Zahlen (also Zahlen der Gestalt ±m/2n), insbesondere am n-ten Tag als jeweils kleinste und größte Zahlen die ganzen Zahlen −n und n. Die Buchstaben m und n stehen im folgenden immer für natürliche Zahlen. Schließlich lassen sich all die an endlichen Tagen entstandenen Zahlen am Tag
für neue Schnittbildungen einsetzen. Dabei entstehen neben ω etwa auch sein Negatives
sowie sein Reziprokes
Derartige Schnitte notiert man auch verkürzt als
Ferner entstehen am Tag ω auch alle noch fehlenden reellen Zahlen. Diese lassen sich als diejenigen Zahlen x charakterisieren, zu denen es eine natürliche Zahl N mit −N< x< N gibt, und für die
gilt bzw., falls man nur an endlichen Tagen erzeugte Zahlen heranziehen will:
Führt man diese Zahlengenese immer weiter, so entstehen sämtliche Ordinalzahlen, wie etwa
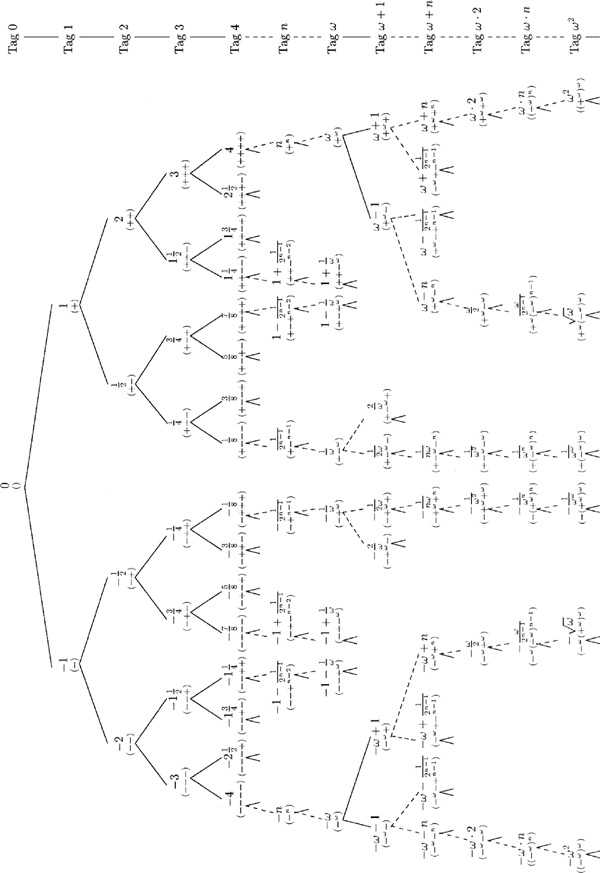
Conways Baum der Zahlen
Die Potenzen von ω entsprechen hierbei speziellen Fällen von Conways ω-Abbildung, die für positive Zahlen x mittels
erklärt ist, wobei r über alle positiven reellen Zahlen läuft. Die ω-Abbildung wird benutzt, um Zahlen nach Potenzen von ω in die sog. Normalform zu entwickeln, vgl. [3].
Es entstehen aber auch nicht-ordinale Zahlen wie
oder auch
sowie die Negativen und Reziproken all dieser Zahlen und auch Zahlen wie
Alle diese Zahlen haben ihren Platz in Conways Baum der Zahlen. In jeder Ebene des Baumes stehen die am zugehörigen Tag α geborenen Zahlen, also gerade diejenigen, deren Vorzeichenentwicklung die ordinale Länge α hat, und zwar der Größe nach sortiert, was der lexikographischen Ordnung der Vorzeichenentwicklung entspricht. In der Abbildung bedeuten die Exponenten n bzw. ω in der Vorzeichenentwicklung die n- bzw. ω-fache Wiederholung einer Zeichenreihe ordinaler Länge.
[1] Alling, N. L.: Foundations of Analysis over surreal number fields. Elsevier Science Publishers Amsterdam, 1987.
[2] Conway, J. H.: Über Zahlen und Spiele. Vieweg Braunschweig, 1983.
[3] Conway, J. H.: On Numbers and Games. A K Peters Natick, Massachusetts, 2001.
[4] Ehrlich, P. (ed): Real Numbers, Generalizations of the reals, and theory of continua. Kluwer Academic Publisher Dordrecht, 1994.
[5] Gonshor, H.: An Introduction to the Theory of Surreal Numbers. Cambridge University Press, 1986.
[6] Knuth, D. E.: Insel der Zahlen. Vieweg Braunschweig, 1978.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.