Lexikon der Mathematik: Tangentenmethode
Verfahren, das gemeinsam mit der Sekantenmethode zur Konstruktion rationaler Punkte einer algebraischen Menge dient.
Zur Erläuterung betrachte man die Bachetschen Gleichung
Die Menge aller reellen Lösungen dieser Gleichung ist ein Kurve C ⊂ ℝ2. Ist (x0, y0) ∈ C, so ist
die Gleichung der Tangente an C in diesem Punkt. Liegt (x, y) sowohl auf der Tagente als auch auf der Kurve C, so muß (x, y) sowohl Gleichung (1) als auch Gleichung (2) erfüllen. Nach kurzer Rechnung erhält man (im Fall y0 ≠ 0) für die x-Koordinate die Gleichung
Daraus ergibt sich neben (x0, y0) noch ein Schnittpunkt der Tangente mit der Kurve, nämlich
Ist (x0, y0) rational mit y0 ≠ 0, so hat man auf diese Weise einen weiteren rationalen Punkt der durch Gleichung (1) gegebenen Kurve gefunden.
Beginnt man z. B. mit dem rationalen Punkt
der Bachetschen Gleichung x3 − y2 = 2, so erhält man auf diese Weise den weiteren rationalen Punkt
der auch von Bachet selbst angegeben wurde.
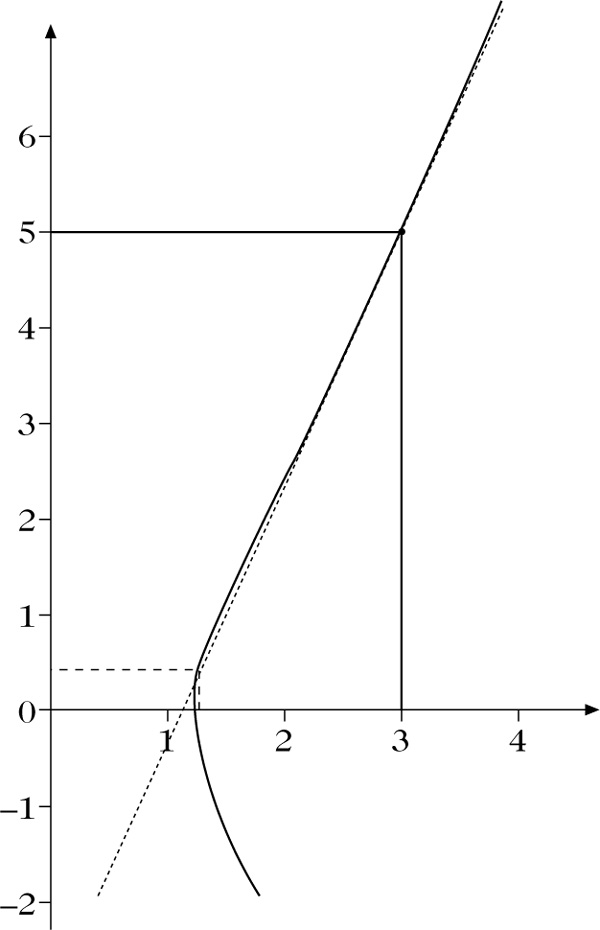
Die Tangente im rationalen Punkt (3, 5) schneidet die Kurve x3 – y2 = 2 in dem weiteren rationalen Punkt \((\frac{129}{100},\frac{383}{10000})\).
Ebenso wie die Sekantenmethode findet sich die Tangentenmethode implizit bereits in der „Arithmetika“ des Diophantos von Alexandria. Bachet gab 1621 diese „Arithmetika“, mit einem ausführlichen Kommentar versehen, heraus; daher wird die Tangentenmethode manchmal auch Bachet zugeschrieben.
Die Tangentenmethode wurde vielfach weiterentwickelt (zunächst von Euler und Cauchy) und wird in komplizierteren und allgemeineren Situationen angewandt, was mitunter technisch recht aufwendig ist.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.