die Frage, ob eine Isomorphie von Kohomologiegruppen H^k (X, ℤ) ≃ H^k (X′, ℤ) für kompakte Kählersche Mannigfaltigkeiten aus einer gegebenen Klasse \({\mathfrak{M}}\), die die Hodge-Struktur respektiert, auch eine Isomorphie der komplexen Mannigfaltigkeiten X, X′ nach sich zieht.

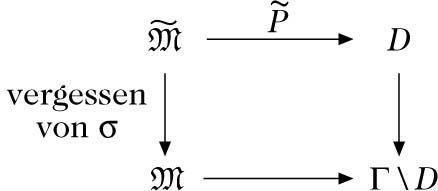
Dazu ist es zweckmäßig, die Periodenabbildung zu definieren: Es sei H ein festes Gitter mit einer (−1)^k-symmetrischen Bilinearform Q : H ⊗ H → ℤ und \(D\subset \check{D}\) der Raum aller polarisierten Hodge-Strukturen vom Gewicht k desselben Typs wie die von \({H}^{k}\text{(}X\text{,}\ {\mathbb{Z}}\text{)}\ \text{(}X\in \ {\mathfrak{M}}\text{)}\) (Variation von Hodge-Strukturen). \(\tilde{{\mathfrak{M}}}\) sei die Menge aller Isomorphieklassen (X, σ), σ : H^k (X, ℤ) / Torsion \(\mathop{\to}\limits^{\sim}H\) (mit Q verträglich) und \({\rm{\Gamma}}\ \text{=}\ {\mathbb{O}}\text{(}H,\ Q\text{)}\). Jedes (X, σ) induziert dann eine Hodge-Struktur auf H, und man erhält Abbildungen:

Eine Variante wird im folgenden geschildert: Auf den X werden durch ein amples Geradenbündel noch Polarisierungen festgelegt. \( {\mathcal L} \), h sei ein fixiertes Element von H, D der Raum aller Hodge-Strukturen mit h ∈ H^m,m, und Γ die Gruppe \({\mathbb{O}}{\text{(}H,\ Q\text{)}}_{h}\) der Automorphismen, die h festlassen. σ erfülle noch die Bedingung \(\sigma ({c}_{1}{({\mathcal L})}^{m})=h\). Es geht dann um die Frage der Injektivität der Periodenabbildung P (oder \(\tilde{P}\)). Meist sind \({\mathfrak{M}}\) und \(\tilde{{\mathfrak{M}}}\) komplexe Räume und P, \(\tilde{P}\) Morphismen komplexer Räume.

Ebenso gibt es eine infinitesimale Variante der Periodenabbildung für eine Kählersche Mannigfaltigkeit X₀. Der Parameterraum der semiuniversellen Deformation (Modulprobleme) von X₀ hat im Ursprung einen zu \({H}^{1}\ ({X}_{0},{{\rm{\Theta}}}_{{X}_{0}})\) kanonisch isomorphen Tangentialraum (durch die Kodaira-Spencer-Abbildung), und die Tangentialabbildung \({T}_{\text{0}}(\tilde{P})\) bildet diesen Raum in den Unterraum \({T}_{\text{hor}}{(D)}_{\tilde{P}(0)}\), der isomorph zu \begin{eqnarray}\displaystyle \sum _{p\gt q}{\text{Hom}}_{Q}({H}^{p,q}({X}_{0}),\ {H}^{p-1,q+1}({X}_{0}))\end{eqnarray} ist (Variation von Hodge-Strukturen). Hier ist Hom_Q der Raum der linearen Abbildungen ϕ mit \begin{eqnarray}Q(\varphi (x),s)+Q(x,\varphi (s))=0.\end{eqnarray}

Diese Abbildung wird durch das Cup-Produkt \begin{eqnarray}{H}^{1}({X}_{0},{{\rm{\Theta}}}_{{X}_{0}})\otimes {H}^{q}({X}_{0},{{\rm{\Omega}}}_{{X}_{0}}^{p})\\ \ \ \ \ \ \ \ \ \ \ \ \ \to {H}^{q+1}({X}_{0},{{\rm{\Theta}}}_{{X}_{0}}\otimes {{\rm{\Omega}}}_{{X}_{0}}^{p})\end{eqnarray} und die durch die Kontraktion \({{\rm{\Theta}}}_{{X}_{0}}\otimes {{\rm{\Omega}}}_{{X}_{0}}^{p}\to {{\rm{\Omega}}}_{{X}_{0}}^{p-1}\) induzierte Abbildung \begin{eqnarray}{H}^{q+1}({X}_{0},{{\rm{\Theta}}}_{{X}_{0}}\otimes {{\rm{\Omega}}}_{{X}_{0}}^{p})\to {H}^{q+1}({X}_{0},{{\rm{\Omega}}}_{{X}_{0}}^{p-1})\end{eqnarray} gegeben. Wenn z. B. \({{\rm{\Omega}}}_{{X}_{0}}^{n}\) ein triviales Geradenbündel ist (n = dim X₀), so liefert die Kontraktion mit einer globalen holomorphen n-Form einen Isomorphismus \({{\rm{\Theta}}}_{{X}_{0}}\to {{\rm{\Omega}}}_{{X}_{0}}^{n-1}\) und einen Isomorphismus \begin{eqnarray}\begin{array}{l}{H}^{1}({X}_{0},{{\rm{\Theta}}}_{{X}_{0}})\to \text{Hom(}{H}^{0}({X}_{0},{{\rm{\Omega}}}_{{X}_{0}}^{n}),\\ \ \ \ \ {H}^{1}({X}_{0},{{\rm{\Omega}}}_{{X}_{0}}^{n-1})),\end{array}\end{eqnarray} also gilt in diesem Fall das infinitesimale Torelli-Theorem. Für Kurven ist die Abbildung \begin{eqnarray}{H}^{1}({X}_{0},{{\rm{\Theta}}}_{{X}_{0}})\to \text{Hom(}{H}^{10},{H}^{0,1})\\ \ \ \ \ ={H}^{0}{({X}_{0},{{\rm{\Omega}}}_{{X}_{0}}^{1})}^{*}\otimes {H}^{1}({X}_{0},{{\mathcal{O}}}_{{X}_{0}})\end{eqnarray}

über Serre-Dualität dual zu der Produktabbildung \begin{eqnarray}{H}^{0}({X}_{0},{{\rm{\Omega}}}_{{X}_{0}}^{1})\otimes {H}^{1}({X}_{0},{{\rm{\Omega}}}_{{X}_{0}}^{1})\to {H}^{0}({X}_{0},{{\rm{\Omega}}}_{{X}_{0}}^{1\otimes 2}),\end{eqnarray} und diese ist für nicht hyperelliptische Kurven vom Geschlecht ≥ 3 surjektiv. Was die Ausgangsfragestellung betrifft, so kann die Antwort positiv oder negativ ausfallen.

Beispiele, in welchen ein Torelli-Satz gilt, sind:

1. Kurven (H¹(X, ℤ));
2. polarisierte abelsche Varietäten (H¹(X, ℤ));
3. K3-Flächen (Klassifikation von Flächen) (H²(X, ℤ));
4. Enriques-Flächen (Klassifikation von Flächen) (H²(X, ℤ)).