eine additive Kategorie \({\mathcal{C}}\) mit Zusatzstruktur. Die Zusatzstruktur besteht aus

(1) einem additiven Automorphismus \(T:{\mathcal{C}}\to {\mathcal{C}}\), dem Translationsfunktor,

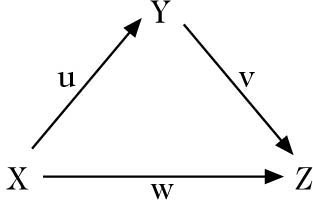
(2) einer ausgewählten Familie von 6-Tupeln (X, Y, Z, u, v, w), die ausgezeichnete Dreiecke genannt werden. Hierbei sind X, Y, Z Objekte von \({\mathcal{C}}\) und u, v, w Morphismen \begin{eqnarray}u:X\to Y,\ \ \ v:Y\to Z,\ \ \ w:Z\to T(X).\end{eqnarray}

Bildlich dargestellt wird solch ein 6-Tupel durch das Dreieck

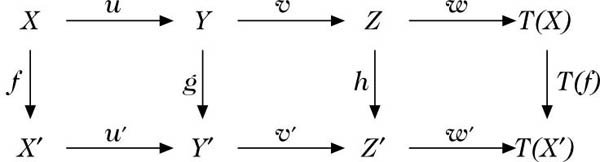
Jedes solche 6-Tupel heißt Dreieck. Ein Morphismus von Dreiecken (X, Y, Z, u, v, w) → (X′, Y′, Z′, u′, v′, w′) ist gegeben durch ein Tripel (f, g, h) von Morphismen f : X → X′, g : Y → Y′, h : Z → Z′, derart, daß das Diagramm

kommutiert. Es sei vorausgesetzt, daß die Axiome (Tr1) bis (Tr4) gelten:

(Tr1) Jedes 6-Tupel der obigen Art, das isomorph zu einem ausgezeichneten Dreieck ist, ist selbst ein ausgezeichnetes Dreieck. Jeder Morphismus u : X → Y kann in ein ausgezeichnetes Dreieck (X, Y, Z, u, v, w) eingebettet werden. Das 6-Tupel (X, X, 0, id_X, 0, 0) ist ein ausgezeichnetes Dreieck.

(Tr2) (X, Y, Z, u, v, w) ist ein ausgezeichnetes Dreieck genau dann, wenn (Y, Z, T(X), v, w, −T(u)) ein ausgezeichnetes Dreieck ist.

(Tr3) Sind zwei ausgezeichnete Dreiecke (X, Y, Z, u, v, w) und (X′, Y′, Z′, u′, v′, w′) und zwei Morphismen f : X → X′, g : Y → Y′ gegeben, die mit u und u′ kommutieren, d. h., gilt u′ ∘ f = g ∘ u, dann gibt es einen Morphismus h : Z → Z′, der (f, g, h) zu einem Morphismus des ersten Dreiecks nach dem zweiten Dreieck macht. (h ist nicht notwendig als eindeutig vorausgesetzt.)

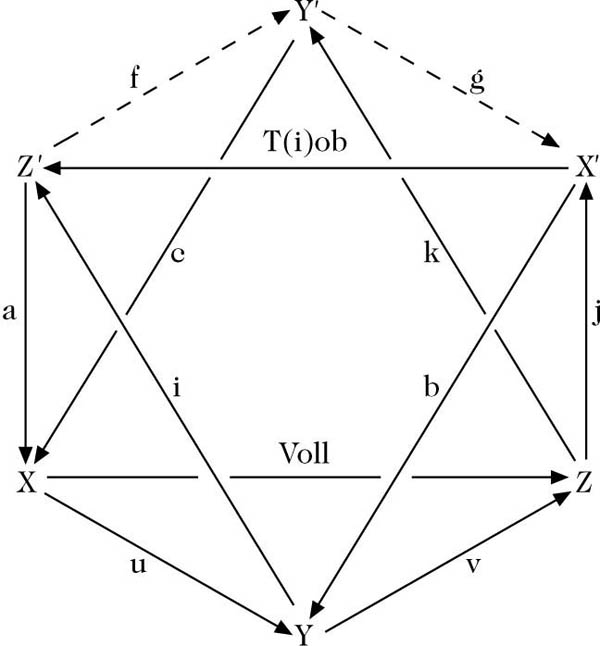
(Tr4) Es gilt das Oktaederaxiom: Sind \begin{eqnarray}\begin{array}{c}{D}_{1}=(X,Y,{Z}^{\prime},u,i,a),\ \ {D}_{2}=(Y,Z,{X}^{\prime},v,j,b),\\ {D}_{3}=(X,Z,{Y}^{\prime},w,k,c)\end{array}\end{eqnarray} drei ausgezeichnete Dreiecke mit w = v ∘ u, dann gibt es zwei Morphismen f : Z′ → Y′, g : Y′ → X′, derart, daß (id_X, v, f) ein Morphismus von D₁ nach D₃ und (u, id_Z, g) ein Morphismus von D₃ nach D₂, und \begin{eqnarray}({Z}^{\prime},{Y}^{\prime},{X}^{\prime},f,g,T(i)\circ b)\end{eqnarray} ein ausgezeichnete Dreieck ist. Dies kann im Bild veranschaulicht werden:

Ein δ-Funktor ist ein additiver Funktor zwischen zwei triangulierten Kategorien, der mit den Translationsfunktoren vertauscht und ausgezeichnete Dreiecke in ausgezeichnete Dreiecke überführt. Ein (kovarianter) Kohomologiefunktor ist ein kovarianter Funktor \(H:{\mathcal{C}}\to {\mathcal{A}}\) von einer triangulierten Kategorie \({\mathcal{C}}\) in eine abelsche Kategorie \({\mathcal{A}}\) für den für jedes ausgezeichnete Dreieck (X, Y, Z, u, v, w) die induzierte lange exakte Sequenz \begin{eqnarray}\to H({T}^{i}X)\to H({T}^{i}Y)\to H({T}^{i}Z)\to H({T}^{i+1}X)\to \end{eqnarray} exakt ist. Analog werden kontravariante Kohomologiefunktoren definiert.