liegt bei einer auf einer Menge D ⊂ ℝ definierten Funktion f : D → ℝ an einer inneren Stelle a ∈ D vor, wenn f an der Stelle a nicht differenzierbar ist, d. h. der Differenzenquotient Q_f (a, x) für x → a nicht konvergiert, aber Q_f (a, x) für x → a bestimmt divergiert, also Q_f (a, x) → −∞ oder Q_f (a, x) → ∞ gilt für x → a. Man schreibt dafür f′(a) = −∞ bzw. f′(a) = ∞, nennt dies eine uneigentliche oder unendliche Ableitung und sagt auch, f habe an der Stelle a eine senkrechte Tangente.

Beispielsweise ist die durch \begin{eqnarray}f(x)=\mathrm{sgn}(x)\sqrt{|x|}\end{eqnarray} definierte Funktion f : ℝ → ℝ stetig und in ℝ \ {0} differenzierbar mit \(f^{\prime} (x)=1/(2\sqrt{|x|})\), aber wegen

lim_x→0Q_f (0, x) = ∞ an der Stelle 0 nicht differenzierbar, sondern uneigentlich differenzierbar.

Bei bestimmter Divergenz von Q_f (a, x) für x ↑ a bzw. x ↓ a spricht man auch von linksseitiger bzw. rechtsseitiger uneigentlicher Differenzierbarkeit von f an der Stelle a und schreibt dafür \({f}_{-}^{\prime}(a)=\infty \), \({f}_{+}^{\prime}(a)=\infty \) usw.. Die durch x ↦ x^2/3 definierte Neilsche Parabeln : ℝ → ℝ ist z.B. linksseitig und rechtsseitig uneigentlich differenzierbar an der Stelle 0, jedoch wegen \({n}_{-}^{\prime}(0)=-\infty \) und \({n}_{+}^{\prime}(0)=\infty \) dort nicht uneigentlich differenzierbar.

Auch etwa an Randstellen eines abgeschlossenen Intervalls D spricht man bei bestimmter Divergenz des Differenzenquotienten von linksseitiger bzw. rechtsseitiger uneigentlicher Differenzierbarkeit.

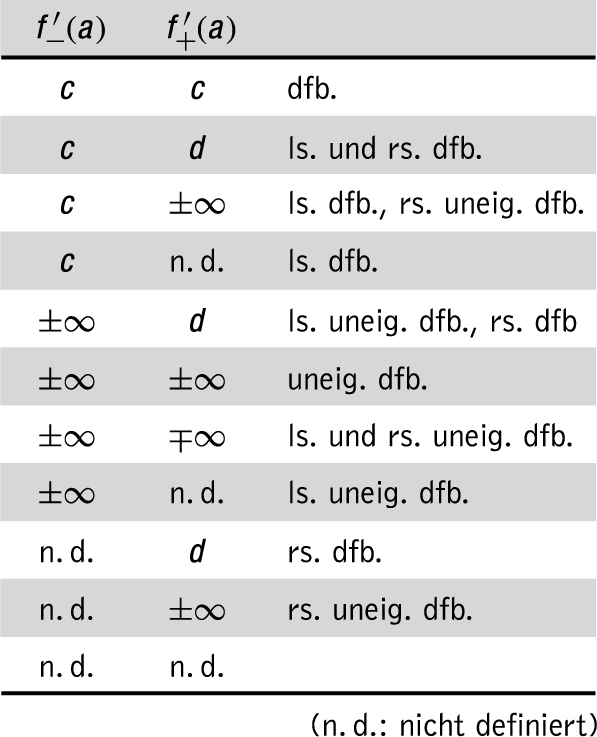
An inneren Stellen a ist jeder der Fälle

mit c, d ∈ ℝ, c ≠ d möglich.

Man beachte, daß aus der uneigentlichen Differenzierbarkeit einer Funktion an einer Stelle nicht ihre Stetigkeit an dieser Stelle folgt, wie man schon an die Signumfunktion an der Stelle 0 sieht.

Mit Hilfe des Mittelwertsatzes der Differentialrechnung kann man zeigen:

Ist f : D → ℝ an einer inneren Stelle a ∈ D stetig und in einer punktierten Umgebung von a differenzierbar (also in (a − ϵ, a + ϵ) \ {a} mit einem geeigneten ϵ > 0), und ist f′(x) für x → a konvergent oder bestimmt divergent, so ist f an der Stelle a differenzierbar bzw. uneigentlich differenzierbar mit\begin{eqnarray}{f}^{\prime}(a)=\mathop{\mathrm{lim}}\limits_{x\to a}{f}^{\prime}(x).\end{eqnarray}

Wie die Signumfunktion zeigt, ist die Voraussetzung der Stetigkeit an der Stelle a wesentlich