zentraler Begriff der Analysis und verwandter Gebiete.

Unstetigkeit einer Funktion f : D → ℝ an einer Stelle x₀ ∈ D ⊂ ℝ besagt, daß f in x₀ nicht stetig, man sagt „unstetig“, ist.

Dies kann unter der Annahme, daß x₀ Häufungspunkt von D ist, verschiedene Gründe haben:

(1) \({\mathrm{lim}}_{x\to {x}_{0}}f(x)\)existiert in ℝ, ist aber verschieden von f(x₀).

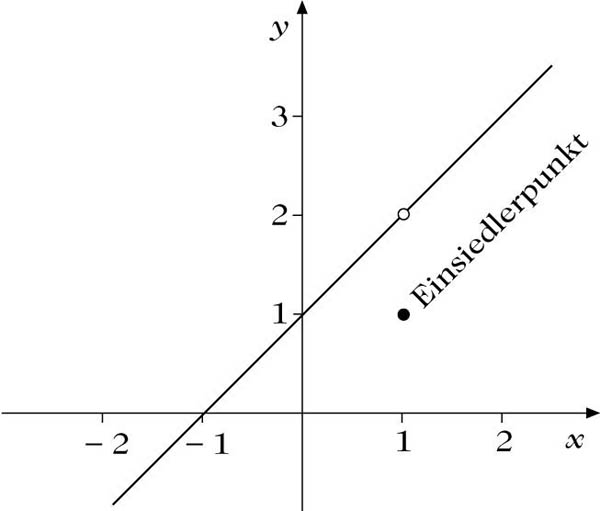
Eine solche Unstetigkeit heißt hebbar, der Punkt (x₀, f(x₀)) Einsiedlerpunkt. Durch Abänderung des Funktionswertes an der Stelle x₀ zu \({\mathrm{lim}}_{x\to {x}_{0}}f(x)\) wird die Funktion stetig in x₀, die Unstetigkeit an dieser Stelle wird so, behoben‘. Man spricht auch von stetiger Ergänzung.

Ein Beispiel: Es sei \begin{eqnarray}f(x):=\left\{\begin{array}{ccc}x+1 &, & x\ne 1\\ 1 &, & x=1\end{array}\right.\end{eqnarray} für x ∈ ℝ. Hier gilt \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{x\to 1}f(x)=2\ne 1=f(1).\end{eqnarray}

Die Unstetigkeit in 1 ist also hebbar, bzw. (1, 1) ist Einsiedlerpunkt.

(2) \({\mathrm{lim}}_{x\to {x}_{0}}f(x)\in \{\infty,\ -\infty \}.\).

Hier ist natürlich eine stetige (reellwertige) Ergänzung nicht möglich.

Ein einfaches Beispiel (mit bestimmter Divergenz gegen ∞) liefert die Funktion \begin{eqnarray}f(x):=\bigg\{\begin{array}{ccc}1/{x}^{2} &, & x\in {\mathbb{R}}\backslash \{0\}\\ 0 &, & x=0\end{array}\end{eqnarray} bei x₀ = 0.

(3) \({\mathrm{lim}}_{x\to {x}_{0}}f(x)\)existiert nicht in ℝ ∪ {∞, −∞}. In diesem Fall kann man noch unterteilen in die beiden Fälle:

(3 a) Es existieren die beiden einseitigen Grenzwerte\begin{eqnarray}\mathop{\mathrm{lim}}\limits_{{x}_{0}\gt x\to {x}_{0}}f(x)\ und\ \mathop{\mathrm{lim}}\limits_{{x}_{0}\lt x\to {x}_{0}}f(x)\end{eqnarray}in ℝ ∪ {−∞, ∞}, diese sind aber verschieden.

Dabei wird davon ausgegangen, daß x₀ Häufungspunkt von D ∩ (−∞, x₀) und von D ∩ (x₀, ∞) ist. Man spricht von einer Sprungstelle (endlicher oder unendlicher Höhe).

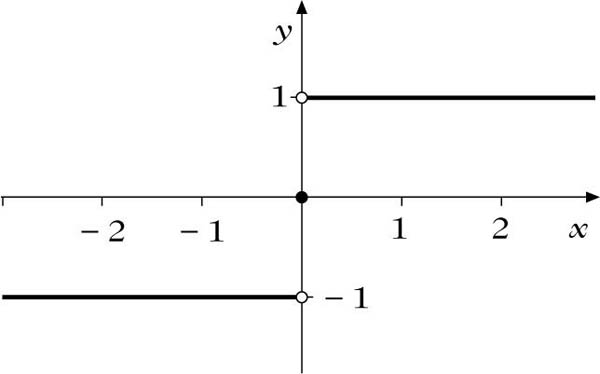
Ein Beispiel wird gegeben durch die Funktion \begin{eqnarray}f(x):={\rm{sgn}}\ (x):=\left\{\begin{array}{rrr}1 &, & x\gt 0\\ 0 &, & x=0\\ -1 &, & x\lt 0\end{array}\right.\end{eqnarray}

Hier sind an der Stelle x₀ = 0 die einseitigen Grenzwerte verschieden und zudem noch beide verschieden vom Funktionswert; 0 ist somit insbesondere Sprungstelle: \begin{eqnarray}\mathop{\mathrm{lim}}\limits_{0\gt x\to 0}f(x)=-1,\ \mathop{\mathrm{lim}}\limits_{0\lt x\to 0}f(x)=1,\ f(0)=0.\end{eqnarray}

Ein einfaches Beispiel für eine Sprungstelle unendliche Höhe liefert die Funktion \begin{eqnarray}f(x):=\bigg\{\begin{array}{ccc}1/x &, & x\in {\mathbb{R}}\backslash \{0\}\\ 0 &, & x=0\end{array}\end{eqnarray} bei x₀ = 0.

(3 b) Mindestens einer der beiden einseitigen Grenzwerte\begin{eqnarray}\mathop{\mathrm{lim}}\limits_{{x}_{0}\gt x\to {x}_{0}}f(x)\ und\ \mathop{\mathrm{lim}}\limits_{{x}_{0}\lt x\to {x}_{0}}f(x)\end{eqnarray}existiert nicht, selbst wenn Werte in ℝ ∪ {−∞, ∞} zugelassen sind.

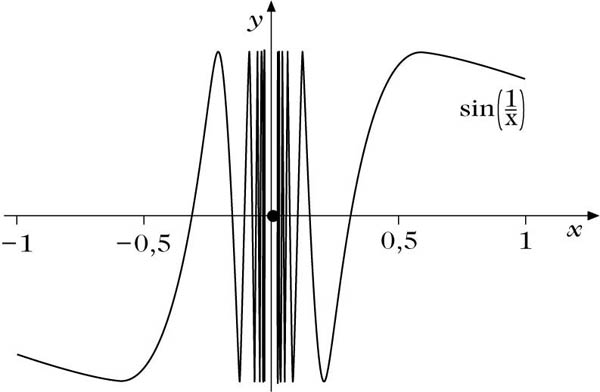
Hier dient die Funktion \begin{eqnarray}f(x):=\left\{\begin{array}{ccc}\sin \left(\frac{1}{x}\right) &, & x\ne 0\\ 0 &, & x=0\end{array}\right.\end{eqnarray} als Beispiel. Für diese Funktion existiert weder der linksnoch der rechtsseitige Grenzwert in 0, denn für \begin{eqnarray}{x}_{n}:=\frac{1}{(2n+\frac{1}{2})\pi}\end{eqnarray} (n ∈ ℕ₀) gelten f(x_n) = 1, f(−x_n) = −1 und x_n → 0.

Für \begin{eqnarray}{u}_{n}:=\frac{1}{(2n-\frac{1}{2})\pi}\end{eqnarray} (n ∈ ℕ) hat man entsprechend f(u_n) = −1, f(−u_n) = 1 und u_n → 0.

(Der engere Bereich um 0 wurde in der Zeichnung ausgespart, weil sonst – wegen der dort immer dichter beieinander liegenden, Schleifen‘ – fast nur noch ein großer schwarzer Balken erkennbar wäre.)

Oft werden auch noch, Lücken‘ fälschlicherweise als Unstetigkeiten bezeichnet. Eine reelle Zahl a heißt genau dann Lücke, wenn α, β ∈ ℝ existieren mit α< β, a ∈ (α, β) \ D, (α, β) \ {a} ⊂ D und lim_x→af(x) existiert in ℝ.

In einer Lücke ist f nicht definiert, die Frage nach der Stetigkeit stellt sich also an einer solchen Stelle gar nicht. Natürlich kann man auch hier nach stetiger Ergänzung fragen.

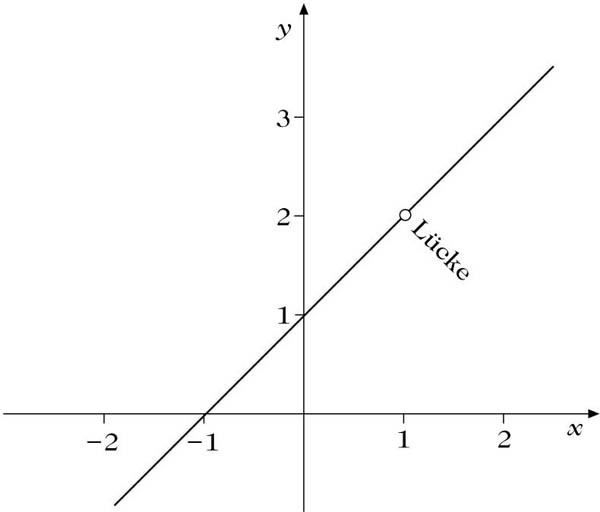
Auch hierzu ein Beispiel: \begin{eqnarray}f(x):=\frac{{x}^{2}-1}{x-1}\ ({\mathbb{R}}\ni x\ne 1).\end{eqnarray}

Für x ∈ D ist f(x) = x + 1.Bis auf die Stelle 1, wo f nicht definiert ist, stimmt also f mit der durch a(x) ≔ x + 1 (x ∈ ℝ) gegebenen Geraden überein. Bei 1 hat f eine Lücke. Die Funktion a ist gerade diejenige, die man durch stetige Ergänzung von f erhält.

Für weitere Information zu diesem Themenkreis siehe auch Stetigkeit.