Begriff aus der algebraischen Geometrie.

Eine Variation von Hodge-Strukturen vom Gewicht k über einer komplexen Mannigfaltigkeit Tist eine lokal konstante Garbe H von endlichdimensionalen reellen Vektorräumen auf T mit einer absteigenden Filtration des zugehörigen holomorphen Vektorbündels \( {\mathcal H} \ =\ {{\mathcal{O}}}_{T}\ {\otimes}_{{\mathbb{Q}}}\ H\) durch holomorphe Unterbündel \({{\mathcal F}}^{p}\ \subset \ {\mathcal H} \) so, daß für jeden Punkt t ∈ T der Vektorraum H_t zusammen mit der Filtration \({({F}_{t}^{p})}_{p}=({{\mathcal F}}^{p}|t)\) auf \({H}_{t}\ {\otimes}_{{\mathbb{R}}}\ {\mathbb{C}}\ =\ {\mathcal H} |\ t\) eine reelle Hodge-Struktur vom Gewicht k ist, und für den flachen holomorphen Zusammenhang \(\nabla =d\otimes I{d}_{H}\) auf \( {\mathcal H} \) gilt: \begin{eqnarray}\nabla ({{\mathcal{F}}}^{p})\subseteq {{\rm{\Omega}}}_{T}^{1}\otimes {{\mathcal{F}}}^{p-1}\end{eqnarray} („Griffiths Transversalitätsbedingung“).

Eine Variaton von polarisierten Hodge-Strukturen ist eine Variation von Hodge-Strukturen \((H,\ {{\mathcal F}}^{p})\) die zusätzlich mit einer lokal konstanten Garbe H_ℤ ⊂ H abelscher Gruppen und einer bilinearen Abbildung Q : H_ℤ ⊗ H_ℤ → ℤ_T (konstante Garbe ℤ auf T) versehen ist, so daß H = H_ℤ ⊗ ℝ gilt, und (H_ℤ, Q) auf jeder Faser eine Polarisierung der reellen Hodge-Struktur \(({H}_{t},\ {F}_{t}^{p})\) induziert.

Die wichtigsten Beispiele für Variationen von Hodge-Strukturen sind von folgender Art:

Sei X ⊂ ℙ^N × T eine abgeschlossene komplexe Untermannigfaltigkeit und f : X → T die Projektion auf T, die als glatt vorausgesetzt sei. X ist also eine Familie glatter projektiver Mannigfaltigkeiten \begin{eqnarray}{\left({X}_{t}={f}^{-1}(t)\right)}_{t\in T}.\end{eqnarray}

Dann ist für jedes k ∈ ℤ die Garbe R^kf_*ℤ_X lokal konstante Garbe mit den Halmen H^k(X_t, ℤ) in t ∈ T, ebenso ihr Bild \begin{eqnarray}{H}_{{\mathbb{Z}}}\subset {R}^{k}{f}_{*}{{\mathbb{Z}}}_{X}\otimes {\mathbb{R}}={R}^{k}{f}_{*}{{\mathbb{R}}}_{X}=H,\end{eqnarray} und \({{\mathcal{O}}}_{T\otimes {\mathbb{R}}}H= {\mathcal H} \) ist die relative de Rham-Kohomologie \begin{eqnarray}{{\mathcal{H}}}_{DR}^{k}(X/S)={{\mathbb{R}}}^{k}{f}_{*}\left({{\rm{\Omega}}}_{X/S}^{\bullet}\right)\end{eqnarray} (die k-te Hyperkohomologie des Komplexes \({{\rm{\Omega}}}_{X/S}^{\bullet}\) der relativen holomorphen Differentialformen von X über S). Der flache Zusammenhang d ⊗ Id_H = ∇ stimmt überein mit dem rein algebraisch definierten Gauß-Manin-Zusammenhang, und die Filtration \({{\mathcal F}}^{p}\) ist die zur Hodge-Spektralfolge (Hyperkohomologie) gehörende Filtration, die sich auch wie folgt ergibt:

Der Komplex \({{\rm{\Omega}}}_{X/S}^{\bullet}\) besitzt eine Filtration durch Unterkomplexe \({F}^{p}{{\rm{\Omega}}}_{X/S}^{\bullet}:\ {({F}^{p}{{\rm{\Omega}}}_{X/S}^{\bullet})}^{j}=0\) für j < p und = \({{\rm{\Omega}}}_{X/S}^{j}\) für j ≥ p (die sogenannte „stupide Filtration“), und \({{\mathcal F}}^{p}\) ist das Bild des induzierten Morphismus’ \begin{eqnarray}{{\mathbb{R}}}^{k}{f}_{*}\left({F}^{p}{{\rm{\Omega}}}_{X/S}^{\bullet}\right)\to {{\mathbb{R}}}^{k}{f}_{*}\left({{\rm{\Omega}}}_{X/S}^{\bullet}\right)={\mathcal{H}}.\end{eqnarray}

Auf diese Weise erhält man eine Variation von Hodge-Strukturen (VHS) \((H,{{\mathcal F}}^{p})\), zusätzlich mit einem Gitter H_Z ⊂ H und einer Bilinearform \begin{eqnarray}\begin{array}{l}Q:{H}_{{\mathbb{Z}}}\otimes {H}_{{\mathbb{Z}}}\to {{\mathbb{Z}}}_{T},\\ Q(\alpha,\beta)=\alpha \cup \beta \cup {c}_{1}{({\mathcal{O}}(1))}^{n-k},\end{array}\end{eqnarray} (\(n=\dim \ {X}_{t};\ {c}_{1}({\mathcal{O}}(1))\) die Chern-Klassen). Die Bilinearform kann allerdings auf den Fasern ausgeartet sein.

Es gibt universelle Variationen von polarisierten Hodge-Strukturen in folgendem Sinne: Wenn H ein konstantes lokales System ist und \({f}^{p}=rg({{\mathcal F}}^{p})\) der Rang von \({{\mathcal F}}^{p}\), so wird die Filtration \({{\mathcal F}}^{p}\) von \( {\mathcal H} \) durch einen Morphismus μ in die Fahnenmannigfaltigkeit \( {\mathcal F} (({f}^{p}),\ {H}_{{\mathbb{C}}})\ =\ {\mathbb{F}}\) aus der universellen Fahne induziert. Wenn H_ℤ, Q Polarisierung ist, so faktorisiert μ über die Untermannigfaltigkeit \(D\subset \check{D}\subset {\mathbb{F}}\), F^p orthogonal zu F^k−p+1 bzgl. Q}, \(D=\{({F}^{p})\in \check{D}|Q{(\sqrt{-1})}^{p-q}\xi,\overline{\xi})\gt 0\ \,\text{f}{\rm\ddot{u}}\text{r}\,\ \xi \in {H}^{p,q}={F}^{p}\cap \overline{{F}^{k-p}}\}\). \(\check{D}\) ist eine homogene algebraische Varietät, auf der die orthogonale Gruppe von Q auf H_ℂ transitiv operiert, und D ist offene Untermannigfaltigkeit von \(\mathop{{D}^{an}}\limits^{\vee}\), auf der \(G({\mathbb{R}})={\mathbb{O}}({H}_{{\mathbb{R}}},Q)\) transitiv operiert.

Die Monodromiegruppe Γ des lokalen Systems H_ℤ einer polarisierten VHS ist eine diskrete Untergruppe von G(ℝ), unter bestimmten Voraussetzungen über T gilt der Monodromiesatz, der die Quasiunipotenz bestimmter Monodromietransformationen beinhaltet.

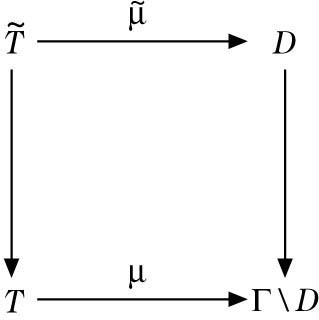
Jede polarisierte VHS über einer analytischen Mannigfaltigkeit T mit der universellen Überlagerung \(\mathop{T}\limits^{\sim}\) induziert einen Morphismus \(\mathop{\mu}\limits^{\sim}:\mathop{T}\limits^{\sim}\to D\) (und μ : T → Γ \ D so, daß das Diagramm kommutativ ist, Γ ist die Monodromiegruppe). Die Griffith-Transversalität drückt sich darin aus, daß die zu \(\mathop{\mu}\limits^{\sim}\) gehörige Tangentialabbildung das Tangentialbündel von \(\mathop{T}\limits^{\sim}\) in ein bestimmtes Unterbündel T_hor(D) ⊂ T(D) des Tangentialbündels an D abbildet: Schreibt man \(\check{D}=G({\mathbb{C}})/B\), B eine Isotropiegruppe eines Punktes 0 ∈ D, dem die Hodge-Struktur \(({H}_{0}^{p.q})\) entspricht, so ist \({\mathfrak{g}}\ =\ \mathrm{Lie}(G({\mathbb{C}}))\subset \mathrm{End}({H}_{{\mathbb{C}}})\) mit einer reellen Hodge-Struktur vom Gewicht 0 versehen durch

\begin{eqnarray}{{\mathfrak{g}}}^{r,-r}=\left\{X\in {\mathfrak{g}}|X({H}_{0}^{pq})\subseteq {H}_{0}^{p+r,q-r}\right\}.\end{eqnarray}

Die Lie-Algebra von B ist \begin{eqnarray}{\mathfrak{b}}={F}^{0}{\mathfrak{g}}=\mathop{\oplus}\limits_{r\ge 0}{{\mathfrak{g}}}^{r,-r},\end{eqnarray} und das Tangentialbündel \(T(\check{D})\) ist das zu der adjungierten Darstellung von B auf \({\mathfrak{g}}/{\mathfrak{b}}\) gehörige homogene Bündel \(G({\mathbb{C}}){\times}^{B}({\mathfrak{g}}/{\mathfrak{b}})\). Das horizontale Unterbündel ist \begin{eqnarray}{T}_{{\rm{hor}}}(\check{D})=G({\mathbb{C}}){\times}^{B}{F}^{-1}({\mathfrak{g}})/{\mathfrak{b}}.\end{eqnarray}

Die Quasiunipotenz der lokalen Monodromie zieht ein bestimmtes Verhalten einer VHS bei Annäherung an Randpunkte nach sich: Wenn T = Δ^*a × T′, \begin{eqnarray}{{\rm{\Delta}}}^{*}=\{z\in {\mathbb{C}},\ 0\lt |z|\lt 1\},\end{eqnarray}T′ kontrahierbar, und \(\mathcal{H}^{a}\times T\text{'}\mathop{\to}\limits^{p}T\) sowie \(\mathcal{H}=\{\tau \in {\mathbb{C}},\ {\rm{Im}}\tau \gt 0\}\) und \begin{eqnarray}p({\tau}_{1},\ldots,{\tau}_{a},{t}^{\prime})=(\exp (2\pi i{\tau}_{1},\ldots,\exp (2\pi i{\tau}_{a}),{t}^{\prime}),\end{eqnarray} und wenn eine reelle VHS mit einer reellen Bilinearform Q gegeben ist, die die Periodenrelationen \begin{eqnarray}Q({{\mathcal{F}}}^{p},{{\mathcal{F}}}^{k-p+1})=0,\ Q(C\xi,\overline{\xi})\gt 0\end{eqnarray} erfüllt, so daß die lokalen Monodromieoperatoren T₁, …,T_a quasiunipotent sind, so gilt:

(1) Das Bündel \( {\mathcal H} \) mit der Filtration \({{\mathcal F}}^{p}\) und der Bilinearform Q läßt sich holomorph auf Δ^a × T′ fortsetzen.

(2) Für die daraus resultierenden nilpotenten Orbits \begin{eqnarray}{N}_{{t}^{\prime}}(\tau)=\exp (\displaystyle \sum {\tau}_{j}{N}_{j})[{{\mathcal{F}}}^{\bullet}|O\times {t}^{\prime}]\end{eqnarray} in \(\check{D}\) gilt: \({N}_{{t}^{\prime}}(\tau)\in D\) für Im(τ_j) ≫ 0 (j = 1, …,a), und für Im(τ_j) → ∞ (j = 1, …,a) konvergiert der Abstand zwischen \({N}_{{t}^{\prime}}(\tau)\) und \(\tilde{\mu}(\tau,{t}^{\prime})\) gegen 0 (in einer präzise beschreibbaren Weise). Dies ist das nilpotente Orbittheorem.

Eine Abbildung \(N:\mathcal{H}^{a}\to \check{D}\) der Form \begin{eqnarray}N(\tau)=\exp \left(\displaystyle \sum _{j=1}^{a}{\tau}_{j}{N}_{j}\right)F\end{eqnarray} mit kommutierenden nilpotenten Transformationen \({N}_{j}\in {{\mathfrak{g}}}_{{\mathbb{R}}}\cap {F}^{-1}{\mathfrak{g}}\), \(F\in \check{D}\), so daß N(τ) ∈ D für Re(τ_j) ≫ 0 (j = 1, …,a) heißt auch nilpotenter Orbit.

Jeder nilpotente Endomorphismus N von H_ℝ definiert eine eindeutig bestimmte aufsteigende Filtration W(N) durch W(N)_n = H_ℝ bzw. W(N)_−n = 0 für Nⁿ = 0, und induktiv, für m ≥ 1, \begin{eqnarray}\begin{array}{rll}{W}_{m-1} & = & {({N}^{m})}^{-1}({W}_{-(m+1)}),\\ {W}_{-m} & = & {N}^{m}({W}_{m}).\end{array}\end{eqnarray}

Sie ist durch die Eigenschaften \begin{eqnarray}\begin{array}{rll}N({W}_{m}) & \subseteq & {W}_{m-2},\\ {N}^{m} & : & {W}_{m}/{W}_{m-1}\mathop{\to}\limits^{\sim}{W}_{-m}/{W}_{-(m+1)}\end{array}\end{eqnarray} charakterisiert. Ist W = W(N)[−k] die um k verschobene Filtration, so gilt: Ist τ ↦ exp(τN)F nilpotenter Orbit, so ist (H_ℝ, W, F) eine über ℝ definierte gemischte Hodge-Struktur und (Q, N) eine Polarisierung von (H_ℝ, W, F).

Letzteres bedeutet: Die Bilinearform Q ist N-invariant, W ist die verschobene Filtration W(N), NF^p ⊆ F^p−1, und Q(·, N^ℓ ·) induziert eine Polarisierung der Hodge-Struktur vom Gewicht ℓ − k auf \begin{eqnarray}{P}_{\ell -k}={\rm{Ker}}\ \left({N}^{\ell +1}:G{r}_{\ell -k}^{W}\to G{r}_{-\ell -k-2}^{W}\right).\end{eqnarray}

Als Grenzfall der Variation von Hodge-Strukturen erhält man also gemischte Hodge-Strukturen. Jede gemischte Hodge-Struktur (H_ℝ, W, F) läßt sich in eine zerfallende gemischte Hodge-Struktur \(({H}_{{\mathbb{R}}},W,\tilde{F})\) degenerieren, d. h. \begin{eqnarray}{H}_{{\mathbb{C}}}\mathop{\oplus}\limits_{p,q}{\tilde{I}}^{pq}\end{eqnarray} mit \begin{eqnarray}{\tilde{F}}^{p}=\displaystyle \sum _{r\ge p}{\tilde{I}}^{r,s},\ {({W}_{\ell})}_{{\mathbb{C}}}=\displaystyle \sum _{p+q\le \ell}{\tilde{I}}^{p,q}.\end{eqnarray}