Lexikon der Mathematik: Versuchsplanung
Die Versuchsplanung (Design of Experiments) ist ein eigenständiges Teilgebiet der Mathematischen Statistik (statistische Versuchsplanung) mit Lösungsansätzen aus der Kombinatorik (kombinatorische Design-Theorie) und der konvexen Analysis.
Fragestellung: Statistische Untersuchungen dienen zur Aufdeckung funktionaler Zusammenhänge zwischen erklärenden Variablen (unabhängige Variablen, exogene Variablen, Einflußfaktoren) und einer abhängigen Variablen (endogene Variable, Ergebnis), wenn die jeweiligen Beobachtungen mit einem Zufallsfehler behaftet sind. Man unterscheidet zwischen Experimenten mit aktiv erhobenen Beobachtungen, bei denen die Einflußfaktoren vom Experimentator eingestellt werden können, und Beobachtungsstudien, bei denen auch die erklärenden Variablen nur passiv beobachtet werden können. Typische Beispiele für Messungen in Experimentalsituationen sind: Auf landwirtschaftlichen Versuchsfeldern der Ernteertrag in Abhängigkeit von Getreidesorten und Düngemitteln, in der medizinischen Forschung der Heilungserfolg in Abhängigkeit von Behandlungen, bei der Entwicklung von Prototypen in der industriellen Produktion die Produktqualität in Abhängigkeit von Prozeßvariablen wie Druck, Temperatur, Prozeßdauer und Mischungsverhältnis von Komponenten, oder in der psychologischen Marktforschung der individuelle Nutzen in Abhängigkeit von Ausstattung und Preis verschiedener dargebotener Alternativen. Experimentalsituationen haben den großen Vorteil, daß durch eine geeignete Auswahl der Versuchseinstellungen für die einzelen Einflußfaktoren eine wesentliche Verbesserung der Qualität des Experiments erreicht werden kann.
Im allgemeinen besteht ein Versuch aus mehreren Einzelexperimenten, die an einzelnen Versuchseinheiten durchgeführt, und für die die Einflußfaktoren auf verschiedene Stufen eingestellt werden können. Zur Beschreibung des Einflusses dieser Faktoren auf das Versuchsergebnis unterscheidet man zwischen Modellen der Varianzanalyse, bei denen alle Faktoren nur auf einigen wenigen Stufen eingestellt werden (z. B. Behandlungen, Weizensorten, Düngemittel), Modellen der Regressionsanalyse, bei denen alle Faktoren über einen Bereich stetig variieren (z. B. Temperatur, Druck oder Dosierungen), und allgemeinen Modellen der Kovarianzanalyse, bei denen beide Sorten von Faktoren auftreten können.
Vorrangig befaßt sich die statistische Versuchsplanung mit der Wahl der Versuchseinstellungen im Hinblick auf eine möglichst große Genauigkeit der statistischen Analyse, wobei der Versuchsumfang als fest vorgegeben vorausgesetzt wird.
Historisches: Obwohl viele Ideen der Versuchsplanung älteren Ursprungs sind, gelten Fisher, 1926, und Yates, 1935, mit der Propagierung der Grundprinzipien Randomisierung, Blockbildung und Wiederholbarkeit als deren Begründer. Erste AnwendungsgebietewarenagrarwissenschaftlicheFeldversuche und Experimente in den Biowissenschaften. Später kamen ingenieur- und wirtschaftswissenschaftliche Fragestellungen hinzu (Taguchi-Ansatz zur Verbesserung der industriellen Produktion, 1980). Kombinatorische Hilfsmittel zur Konstruktion möglichst symmetrischer Anordnungen (z. B. Euler, 1782) fanden bereits frühzeitig Anwendung auf varianzanalytische Modelle. Fragen der optimalen Versuchsplanung bei Regressionsmodellen wurden seit 1918 in der Literatur behandelt. Die Formalisierung der statistischen Versuchsplanung leistete Kiefer 1959 mit der Einführung des Konzeptes verallgemeinerter Versuchspläne, das eine Einbettung der Optimierungsprobleme in die konvexe Analysis erlaubte. In den darauf folgenden Jahren wurden optimale Versuchspläne für große Klassen von allgemeinen linearen und nichtlinearen Modelle bis hin zu nichtparametrischen (modellfreien) Ansätzen bestimmt.
Grundprinzipien: Randomisierung, d. h. zufällige Zuordnung von Versuchseinstellungen zu den einzelnen Versuchseinheiten, und Blockbildung, d. h. Zusammenfassung gleichartiger Versuchseinheiten, sind allgemein anerkannte Prinzipien zum Ausschalten systematischer individueller Effekte bzw. zur Reduktion der Variabilität zwischen verschiedenen Versuchseinheiten. Die Randomisierung läßt sich als Spezialfall des allgemeineren Konzepts der Symmetrisierung interpretieren, das auf Ideen der In- bzw. Äquivarianz beruht: In vielen Experimentalsituationen gibt es natürliche Transformationen des Versuchsbereichs (Permutationen von Stufen oder Faktoren, Spiegelungen, Drehungen), für die die Qualität der statistischen Analyse sich nicht ändert. Daher sollten effiziente Versuchspläne selbst invariant bezüglich dieser Transformationen sein oder zumindest eine invariante Analyse erlauben (fraktionelle Strukturen). Die Blockbildung dient der gleichmäßigen Verteilung der Versuchseinstellungen auf homogene Gruppen (Blöcke) von Versuchseinheiten. Insbesondere in biowissenschaftlichen Untersuchungen liegen oft paarige Beobachtungen (Blöcke der Größe 2) vor, etwa wenn Paare von Augen oder Ohren eines Individuums untersucht werden. In agrarwissenschaftlichen Untersuchungen werden Versuchsfelder mit einer möglichst homogenen Bodenbeschaffenheit als Block betrachtet und in Parzellen als Versuchseinheiten aufgeteilt. Als Blockfaktoren können auch zusätzliche Eigenschaften der Versuchseinheiten gewertet werden, deren Einfluß auf das Versuchsergebnis nicht untersucht werden soll (etwa das Geschlecht, das Alter oder der Erkrankungszustand von Versuchspersonen). Die entsprechenden Blockeffekte sind nicht von Interesse und gehen als Störparameter in das Experiment ein. Eine Minimalforderung an die Versuchsplanung ist hierbei, daß trotz dieser störenden Blockeffekte die Modellparameter für die zu untersuchenden Einflußfaktoren identifizierbar (schätzbar, testbar) sind.
Kombinatorische Versuchsplanung : Aufgabenstellung kombinatorischer Ansätze ist einerseits eine möglichst gleichmäßige Anordnung der Stufen innerhalb einzelner Faktoren (Balanciertheit) und andererseits Unabhängigkeit zwischen den verschiedenen Faktoren (Orthogonalität). Aufgrund ihrer Struktur werden kombinatorische Versuchspläne vorrangig in Modellen der Varianzanalyse angewandt. Blockpläne dienen der Ausschaltung störender Blockeffekte. Wenn die Anzahl der Stufen die Blockgröße überschreitet, weisen vollständig balancierte, unvollständige Blockpläne (BIBD) balancierte Randverteilungen für die einzelnen Stufen bzw. Stufenkombinationen auf. Zur Konstruktion kombinatorischer Versuchspläne werden algebraische Strukturen und Elemente der Gruppentheorie (Galoisfelder, projektive Geometrie) als Hilfsmittel herangezogen. Ein typisches Beispiel balancierter Versuchspläne für drei Faktoren, die jeweils über die gleiche Anzahl s von Stufen variieren können, sind Lateinische Quadrate: Jede Zeile bzw. Spalte einer s × s-Tafel entspricht einer Stufe der ersten beiden Faktoren, während die Buchstaben in der Tafel die Stufen des dritten Faktors bezeichnen: jeder Buchstabe darf nur einmal in jeder Zeile und in jeder Spalte auftreten.
Lateinisches Quadrat (4 × 4)
Kann ein weiteres Alphabet so hinzugefügt werden, daß auch die Buchstabenkombinationen in den einzelnen Einträgen genau einmal vorkommen ergibt sich ein Griechisch-Lateinisches Quadrat, wobei die Buchstaben des neuen Alphabets die Stufen eines vierten Faktors sind.
Lateinische und Griechisch-Lateinische Quadrate sind Spezialfälle von Orthogonalen Feldern der Stärke 2: In einem Orthogonalen Feld der Stärke t tritt jede Stufenkombination von je t Faktoren genau einmal auf. Für t = 4 sind neben Haupteffekten auch Zwei-Faktor-Wechselwirkungen identifizierbar. Besitzen alle Faktoren nur zwei Stufen, können balancierte (fraktionell faktorielle) Versuchspläne mit Hilfe von Hadamard-Matrizen konstruiert werden. Alle Einträge einer Hadamard-Matrix sind entweder +1 oder −1 und je zwei Spalten sind orthogonal, d. h. das Skalarprodukt je zweier Spalten ist 0.
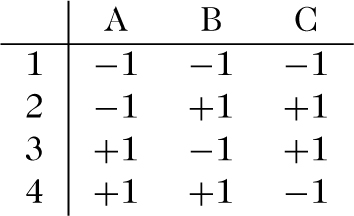
23−1-fraktionell faktorieller Versuchsplan vom Umfang 4 für 3 Faktoren
Einzelne Spalten einer Hadamard-Matrix werden Faktoren zugeordnet, wobei deren beiden Stufen jeweils als ±1 codiert sind. Jede Zeile gibt dann die Versuchseinstellungen für ein Einzelexperiment an. Alias-Strukturen dienen zur Charakterisierung der Maskierung von Haupteffekten oder Wechselwirkungen. Die Resolution eines faktoriellen Plans beschreibt, bis zu welchem Wechselwirkungsgrad Modellparameter noch identifizierbar sind. Fraktionell faktorielle Versuchspläne finden Anwendungen in diskretisierten multiplen Regressionsmodellen und als Wiegepläne für das Verteilen von Gewichten auf die Schalen einer Waage.
Optimale Versuchsplanung : Ziel der optimalen Versuchsplanung ist es, Versuchseinstellungen zu finden, die eine möglichst effiziente statistische Analyse des zugrunde liegenden Modells erlauben. Dies soll am Beispiel der Steigung bei einer linearen Regression \(Y={\beta}_{1}+{\beta}_{2}x+\varepsilon \) illustriert werden: Es liegen Beobachtungspaare (xi, Yi) vor, wobei Yi die abhängige Variable bei gegebener Versuchseinstellung xi ist. Die Kleinstquadratsummenschätzung für die Steigung β2 der Regressionsgerade berechnet sich zu
Im allgemeinen wird der funktionale Zusammenhang zwischen den Versuchsbedingungen x und den Beobachtungen Y durch eine Wirkungsfunktion n beschrieben, \(Y(x)=\eta (x,\beta)+\varepsilon \), wobei ϵ den Beobachtungsfehler bezeichnet und die strukturelle Gestalt von η bis auf einen unbekannten Parameter(vektor) β spezifiziert ist. Die Versuchseinstellung x aus dem Versuchsbereich \({\mathcal{X}}\) selbst kann mehrdimensional sein und mehrere Einflußfaktoren repräsentieren. Die bezüglich Fragestellungen der Versuchsplanung meistuntersuchte Modellklasse ist das allgemeine lineare Modell
Erstrebenswert ist eine Optimierung der Kovarianzmatrix im positiv-semidefiniten Sinn, so daß die Varianz \(V({c}^{\top}\hat{\beta})\) für alle eindimensionalen Aspekte \({c}^{\top}\beta \) gleichzeitig minimal würde. Dies ist jedoch im allgemeinen nicht möglich. Daher werden als Kriterien verschiedene Funktionale der Kovarianzmatrix betrachtet, die optimiert werden sollen: Das aufgrund seiner guten analytischen Eigenschaften populärste Kriterium ist das DeterminantenKriterium (D-Kriterium). Weitere, häufig verwendete Kriterien sind die Spur der Kovarianzmatrix (A-Kriterium, average variance) oder ein Minimax-Kriterium für eindimensionale Aspekte,
Weitere Kriterien untersuchen Teilaspekte Aβ des Parameters, wobei A eine (s ×p)-Matrix ist, zum Beispiel die Determinante der Kovarianzmatrix cov \((A\hat{\beta})={\sigma}^{2}AM{({x}_{1},\mathrm{\ldots}{x}_{n})}^{-1}{A}^{\top}\) (DA-Kriterium, bzw. speziell Ds-Kriterium für die ersten s Komponenten von β, Aβ = (β1,…,βs)). Besonderes Interesse gilt der Minimierung der Varianz \(V({c}^{\top}\hat{\beta})={\sigma}^{2}{c}^{\top}M{({x}_{1},\mathrm{\ldots}{x}_{n})}^{-1}c\) eindimensionaler Aspekte (c-Kriterium).
Das Auffinden eines optimalen Versuchsplans ist von seiner Struktur her ein Problem der diskreten Optimierung. Um zusätzlich analytische Ansätze nutzen zu können, werden verallgemeinerte Versuchspläne eingeführt: Zu einem Versuchsplan (x1,…,xn) mit nicht notwendig verschiedenen Versuchseinstellungen wird ein verallgemeinerter Versuchsplan ξ über \(\xi ({x}_{i})={n}_{i}/n\) definiert, wobei ni die Anzahl der Replikationen der Versuchseinstellung xi ist, \(\sum \xi ({x}_{i})=1\). Mit \(M\xi =\sum \xi (x)f(x)f{(x)}^{\top}\) bezeichnet man die standardisierte Informationsmatrix, und entsprechend mit \(d(x;\xi)=f{(x)}^{\top}M{(\xi)}^{-1}f(x)\) die standardisierte Varianzfunktion. Offensichtlich gilt \(M(\xi)=\frac{1}{n}M({x}_{1},\mathrm{\ldots},{x}_{n})\) und \(d(x;\xi)=nd(x;{x}_{1},\mathrm{\ldots},{x}_{n})\) Nach Verzicht auf die Ganzzahligkeit der Replikationen \(n\xi (x)\) ist die Gesamtheit der verallgemeinerten Versuchspläne eine konvexe Menge, und es können Methoden der konvexen Optimierung angewandt werden. Die Optimalitätskriterien lassen sich zumeist als konvexe Funktionale Φ des Versuchsplans darstellen, mit Richtungsableitungen
Ein verallgemeinerter Versuchsplan ξ*minimiert Φ genau dann, wenn \({\Phi}{^{\prime}}(\xi^* ;x)\ge 0\)für alle \(x\in {\mathcal{X}}\).
Zusätzlich verschwindet die Richtungsableitung \({\Phi}{^{\prime}}(\xi^* ;x)=0\) für alle Trägerpunkte x von ξ, \(\xi (x)\gt 0\). Für das D-Kriterium ergibt sich daraus der Äquivalenzsatz von Kiefer und Wolfowitz:
Ein verallgemeinerter Versuchsplan ξ* ist D-optimal genau dann, wenn ξ* Goptimal ist.
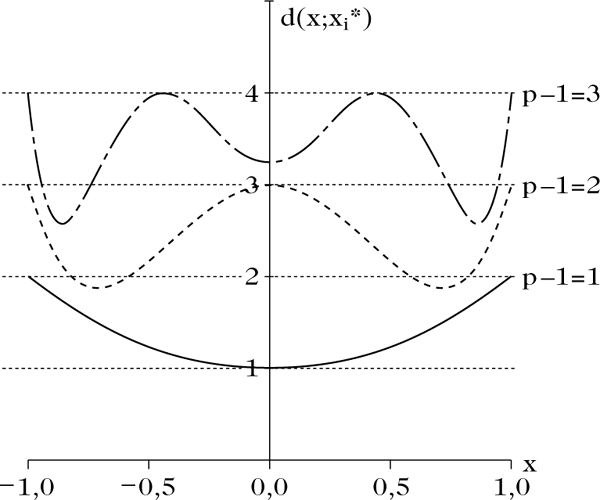
Für einen D- bzw. G-optimalen Plan gilt, daß die Varianzfunktion durch die Anzahl der Parameter beschränkt ist, d(x, f*) ≤ p, mit Gleichheit in den Trägerpunkten. Der Äquivalenzsatz dient vorrangig der Verifikation der Optimalität eines vorgegebenen Versuchsplans. Die Bedingung d(x, f*) = p in den Trägerpunkten kann jedoch auch bei der Konstruktion genutzt werden, wie folgendes Beispiel zeigt: Für polynomiale Regression \(Y(x)={\beta}_{1}+{\beta}_{2}x+\cdots +{\beta}_{p}{x}^{p-1}+\varepsilon \) ist die Varianzfunktion d(x; ξ) ein Polynom vom Grad 2p − 2 in x. Der Versuchsbereich \({\mathcal{X}}\) ist üblicherweise ein abgeschlossenes Intervall. Nach dem Hauptsatz der Algebra besitzt die Varianzfunktion genau p Maxima mit d(x; ξ*) = p auf dem Intervall \({\mathcal{X}}\). Damit hat der optimale Versuchsplan ξ* minimale Anzahl von Trägerpunkten und die Gewichte ξ(x) und Trägerpunkte können getrennt optimiert werden. Insbesondere besitzt der optimale Plan gleiche Gewichte ξ*(x) = 1/p auf allen Trägerpunkten.
Allgemein bestehen über Eigenschaften der Varianzfunktion Zusammenhänge zur Approximationstheorie (Tschebyschew-Systeme), und dort entwickelte Methoden finden in der Versuchsplanung Anwendung. In komplexeren Situationen, in denen es häufig keine expliziten Lösungen für das Versuchsplanungsproblem gibt, können effiziente Pläne mit Hilfe von Optimierungsalgorithmen erzeugt werden, die wie die Methode des steilsten Anstiegs auf den Richtungsableitungen basieren (Algorithmus von Fedorow und Wynn). Über die Richtungsableitungen lassen sich Abschätzungen für die Effizienz eff \((\xi)=\Phi (\xi)/\Phi (\xi^*)\) eines Versuchsplans im Vergleich zum jeweiligen Φ-optimalen Plan ξ* basierend auf der Konkavität des Informationsfunktionals 1/Φ(ξ) herleiten. Zum Beispiel ist die Effizienz bezüglich des D-Kriteriums immer mindestens so groß wie die Effizienz bezüglich des G-Kriteriums,
Varianzfunktionen bei polynomialer Regression, p − 1 = 1, 2, 3, D(G)-optimaler Versuchsplan.
Sei γ > 0 so gewählt, daß γc auf dem Rand der Elfving-Menge liegt. Dann gibt es Versuchseinstellungen x1,…,xnund Gewichte w1,…,wnmit \(\gamma c=\sum {z}_{i}{w}_{i}f({x}_{i})\)für Vorzeichen z1,…,zn = ±1, und der verallgemeinerte Versuchsplan ξ*mit ξ*(xi) = wiist c-optimal.
Der Äquivalenzsatz von Silvey und Sibson setzt das D-Kriterium in Beziehung zur Elfving-Menge: Beschreibt \({c}^{{\rm T}}Jc=p\) das Ellipsoid mit geringstem Volumen, das die Elfving-Menge umschließt, dann ist J = M(ξ*)−1 die Inverse der Informationsmatrix des D-optimalen Plans ξ*, und das Ellipsoid berührt die Elfving-Menge in den Trägerpunkten von ξ*.
Ein allgemeines Konstruktionsprinzip für optimale Versuchspläne ist Symmetrisierung, die In- und Äquivarianz von Modell und Kriterien bezüglich natürlicher Transformationen des Versuchsbereichs ausnutzt. Für Modelle der Varianzanalyse sind daher balancierte Pläne optimal. Regressionsmodelle sind zumeist invariant bezüglich Spiegelungen oder Drehungen des Versuchsbereichs, sodaß man sich bei der Suche nach optimalen Plänen auf die wesentlich vollständige Klasse derjenigen Pläne beschränken kann, die symmetrisch bezüglich dieser Transformationen sind. Dies gilt insbesondere für das D-Kriterium sowie für alle auf der Varianzfunktion basierender Kriterien, da diese Invarianz gegenüber beliebigen linearen Transformationen aufweisen. Insbesondere läßt sich für invariante Kriterien die Optimierung durch Orthogonalisierung auf eine kanonische Form reduzieren. Im allgemeinen gilt dies nicht für A- und E-optimale Pläne, die von der Parametrisierung abhängen und nur gegenüber orthogonalen Transformationen invariant sind.
Elfving-Menge fur quadratische Regression \(Y={\beta}_{1}x+{\beta}_{2}{x}^{2}+\varepsilon \) durch den Ursprung mit kleinster umschliesender Ellipse.
In multifaktoriellen Modellen sind häufig Produktpläne optimal: Für zwei Einflußfaktoren, x = (s, t) ist der Produktplan \(\xi ={\xi}_{1}\otimes {\xi}_{2}\) der marginalen Versuchspläne ξ1 und ξ2 für die einzelnen Einflußgrößen s bzw. t definiert durch \({\xi}_{1}\otimes {\xi}_{2}(x)={\xi}_{1}(s){\xi}_{2}(t).\) Unter anderem kann man in additiven Modellen \(Y(s,t)=\mu +{f}_{1}{(}^{\text T}{\beta}_{1}+{f}_{2}{(}^{\text T}{\beta}_{2}+\varepsilon \) ohne Wechselwirkungen, und in Kronecker-Produkt-Modellen \(Y(s,t)={(}{{f}_{1}(s)}{f}_{1}(t))^\text T\beta +\varepsilon \) mit vollständigen Wechselwirkungen die Suche nach optimalen Plänen auf Produktpläne beschränken, und die Optimierung kann auf marginale Modelle mit nur einem Einflußfaktor zurückgeführt werden. Damit erweisen sich faktorielle Pläne und Orthogonale Felder als optimal in Modellen der Varianzanalyse.
Bei Heteroskedatizität hängt die Fehlervarianz von den Versuchseinstellungen ab, V (ε(x)) = σ2(x). Häufig ist nur deren Struktur bekannt, beispielsweise in loglinearen Varianzmodellen \({\sigma}^{2}(x)=\exp (h{(}^{\text T}\vartheta)\) mit unbekanntem Parameter ϑ. Da die Fehlervarianz in die Informations-matrix
In der allgemeinen Situation nichtlinearer Regression, \(Y(x)=\eta (x,\beta)+\varepsilon, \) ist unter Regularitätsvoraussetzungen die Maximum-Likelihood-Schätzung asymptotisch normal-verteilt,
Weitere, aktuelle Fragestellungen der Versuchsplanung befassen sich unter anderem mit Modelldiskriminierung, Screening zum Auffinden relevanter Faktoren, Identifizierbarkeit von Modellen bei gegebenem Versuchsplan unter Verwendung von Gröbner-Basen, nichtparametrischer Regression, räumlich-zeitlichen Abhängigkeitsstrukturen zwischen den einzelnen Versuchseinheiten (Meßwiederholungen, Zeitreihen, räumliche Prozesse) und adaptiven, sequentiellen Ansätzen.
Unter dem Begriff der adaptiven bzw. sequentiellen Versuchsplanung werden eine Reihe unterschiedlicher Planungsansätze zusammengefaßt: Zweistufige Verfahren bei unbekannten Systemparametern, Interimsanalysen, Up-and-Down-Verfahren zur Dosis-Wirkungsbestimmung (stochastische Approximation), randomisierte Play-the-Winner-Regeln und verallgemeinerte Polya-Urnen, sequentielle Versuchsplanung in nichtlinearen Situationen und adaptive Kontrolle. Allen diesen Verfahren ist gemeinsam, daß Vorinformationen aus vorangegangenen Teilen des Gesamtexperiments genutzt werden, um während des Versuchsverlaufs bessere Versuchseinstellungen auszuwählen oder den Versuchsumfang der tatsächlichen Beobachtungssituation anzupassen.
Literatur
[1] Bandemer, H.; Bellmann, A.: Statistische Versuchsplanung. Teubner-Verlag Stuttgart, 1994.
[2] Cox, D.R.; Reid, N.: The Theory of the Design of Experiments. Chapman & Hall/CRC Boca Raton, 2000.
[3] Pukelsheim, F.: Optimal Design of Experiments. Wiley New York, 1993.
[4] Raghavarao, D.: Constructions and Combinatorial Problems in Design of Experiments. Wiley New York, 1971.
[5] Schwabe, R.: Optimum Designs for Multi-Factor Models. Springer New York, 1996.


Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.