Lexikon der Mathematik: Wavelet
Das Interesse an Wavelets begann etwa um 1980 und wuchs seitdem bis heute (2002) kontinuierlich an. Einige zentrale Ideen der Wavelettheorie existierten auf die eine oder andere Art schon früher in diversen Disziplinen.
Zu Beginn der 1980er Jahre verwendeten Wissenschaftler Wavelets – frz. Ondelettes – als Alternative zur Fourier-Analyse beispielsweise bei der Analyse akustischer oder seismischer Signale. Bei der klassischen Fourierzerlegung einer Funktion ist es nicht möglich, lokale Eigenschaften einer Funktion alleine aufgrund der Kenntnis einiger Fourierkoeffizienten zu analysieren. Demgegenüber hat die Wavelet-Zerlegung einen Vorteil: Die Waveletko-effizienten spiegeln einfach, zuverlässig und präzise die Eigenschaften der zu analysierenden Funktion wider. Anstatt mit den unendlich ausgedehnten Sinus- und Cosinusfunktionen arbeitet man bei der Wavelet-Analyse mit Translationen und Dilatationen einer einzigen Grundfunktion, dem Wavelet (auch mother wavelet genannt).
Vorteilhaft ist, wenn man gut lokalisierte Funktionen verwenden kann. In diesem Fall haben kleine Änderungen im Signal nur kleine Auswirkungen auf die Koeffizienten in der Waveletdar-stellung. Daß solche gut lokalisierten Wavelets, also Funktionen mit kompaktem Träger, existieren, die darüberhinaus auch über eine gewisse Glattheit verfügen, ist nicht von vornherein klar. 1987 wurden Wavelets mit kompaktem Träger und beliebiger Glattheit konstruiert. Dies hat wesentlich zum Erfolg der Waveletmethoden beigetragen.
Historisches
Als erste orthonormale Waveletbasis kann die 1910 von A. Haar konstruierte Haar-Basis angesehen werden. Das Haar-Wavelet h für den Hilbertraum L2(ℝ) ist definiert als
Ausgehend vom mother wavelet h wird eine Orthonormalbasis des L2(ℝ) durch Translation und Dilatation der Funktion h gewonnen. Eine weitere Orthonormalbasis des \({L}_{2}\) wurde 1923 von Walsh konstruiert. Auch diese kann im Nachhinein als eine typische Basis aus sogenannten Wavelet-Paketen (wavelet packets) interpretiert werden.
Nach diesen beiden klassischen Beispielen gab es zahlreiche Entwicklungen in Mathematik und Ingenieurwissenschaften, die letztlich zur Etablierung der Wavelettheorie beigetragen haben. Wesentliche Impulse kamen aus der Spline-Approximationstheorie, der Signal- und Bildverarbeitung (Laplace-Pyramide, Filtertechniken), sowie der harmonischen Analysis. Der Begriff Wavelet wurde ca. 1982 in Frankreich von dem Geophysiker J. Morlet und dem mathematischen Physiker A. Grossmann eingeführt.
Der französische Mathematiker Yves Meyer ist als einer derjenigen Wissenschaftler anzusehen, die die mathematisch fundierte Grundlegung der Wavelettheorie entscheidend geprägt haben. 1985 konstruierte er eine Waveletbasis mit den in mathematischer Hinsicht interessanten Eigenschaften Glattheit und Orthogonalität. Ebenfalls in dieser Zeit wurde von S. Mallat und Y. Meyer ein wichtiges Fundament und zugleich ein wesentliches Hilfmittel für die Konstruktion von Wavelets geschaffen, die multiresolution analysis oder Multiskalenzer-legung.
Die erste Waveletbasis, bestehend aus orthogonalen, beliebig glatten Funktionen mit kompakten Trägern, wurde schließlich von Ingrid Daube- chies 1987 konstruiert. Für viele Anwendungen ist die Eigenschaft der Daubechies-Wavelets, kompakten Träger zu haben, von besonderem Interesse. Speziell bewirken bei Verwendung gut lokalisierter Wavelets kleine Änderungen im Signal nur kleine Änderungen in wenigen Koeffizienten der Wavelet-darstellung.
Was ist ein Wavelet?
Eine Funktion ψ, von der ausgehend durch Translationen und Dilatationen eine Familie {ψa,b} mit
erzeugt wird, heißt Wavelet. Man nennt ψ auch mother wavelet.
Dabei heißt \(a\in {\mathbb{R}}\backslash \{0\}\) der Skalenparameter und \(b\in {\mathbb{R}}\) der Verschiebungsparameter. Hat man ein geeignetes Wavelet gewählt, können ähnlich wie mit Fourieranalyse auch mit Hilfe einer Wavelet-zerlegung Funktionen analysiert werden. Skalenwerte a mit |a| >> 1 liefern eine breitere Funktion und dienen der Erfassung langwelliger Anteile der zu analysierenden Funktion, kleine Skalenparameter mit |a| << 1 liefern sehr schmale Wavelets und erfassen lokal präzise hochfrequente Funktionsanteile. Der Vorfaktor |a|-1/2 dient der Normierung, damit \(\Vert \psi \Vert =1\) gilt.
Es gibt eine Vielzahl unterschiedlicher Wavelets, prinzipiell zugelassen sind alle quadratintegrierba-ren Funktionen \(\psi \in {L}_{2}({\mathbb{R}})\), die die Zulässigkeitsbe-dingung
erfüllen. Eine wichtige Anwendung von Wavelets ist die Analyse und Approximation von Funktionen bzw. diskreten Signalen. Dazu müssen geeignete Basen {ψa,b} (Wavelet-Basis) aus Wavelets konstruiert werden. Für praktische Anwendungen wird häufig eine Diskretisierung der Waveletfunktion ψ vorgenommen. Gängig ist die Festlegung a = 2 und b = 1, in diesem speziellen Fall bildet die Familie
eine orthonormale Basis des \({L}_{2}({\mathbb{R}})\).
Die Wavelet-Transformierte einer Funktion hängt von der Wahl des Wavelets ψ ab. Es steht eine Vielzahl verschiedener Wavelets zur Verfügung. Mit Hilfe der schnellen Wavelet-Transformation werden einer Funktion ihre Waveletkoeffizienten zugeordnet, die zur Analyse derselben verwendet werden können. Mit einer entsprechenden Rücktransformation wird die Synthese der Funktion aus den Waveletkoeffizi-enten vorgenommen. Bei der Auswahl eines geeigneten Wavelets hat man im Gegensatz zur Fourieranalyse, wo die Basisfunktionen feststehen, viel Freiheit. In der Praxis sind folgende Charakteristika von ψ von Interesse:
- Hat ψ kompakten Träger?
- Bildet die Menge
- Verfügt ψ über eine gewisse Anzahl verschwindender Momente?
Die Anzahl der verschwindenden Momente spielt bei der Kompression von Daten eine Rolle. Hat ein Wavelet eine genügend große Anzahl verschwindender Momente, so sind die Waveletkoeffizienten in glatten Bereichen der zu analysierenden Funktion klein – dort, wo Singularitäten auftreten, sind sie dagegen groß. Dieser Effekt ist für die Datenkompression, bei der kleine Koeffizienten vernachlässigt werden, von Interesse.
Multiskalenzerlegung
Die Konstruktion von Wavelets wird zumeist mit Hilfe der Multiskalenzer-legung \({\{{V}_{j}\}}_{j\in {\mathbb{Z}}}\) eines Funktionenraums, z. B. des \({L}_{2}({\mathbb{R}})\), durchgeführt. Wichtig für eine solche Zerlegung ist eine Skalierungsfunktion ϕ, deren ganzzahligen Translate den Grundraum V0 der Multi-skalenzerlegung aufspannen:
Die Verfeinerungsgleichung und die Orthogona-litätbedingung führen zu Bedingungen an die Wave-letkoeffzienten
Viele Wavelettypen, z. B. die Daubechies-Wavelets, sind allein über ihre Koeffizienten gegeben.
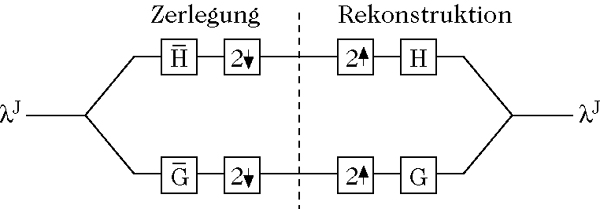
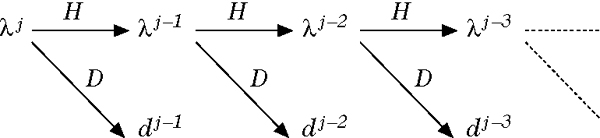
Die Multiskalenzerlegung führt auch zu einem hierarchischen Schema für die Berechnung der Waveletkoeffizienten eines Eingabesignals f. In der Elektrotechnik spricht man von der Zerlegung in Teilbänder (subband coding) mit exakter Rekonstruktion. Das Vorgehen ist in der Abbildung schematisch dargestellt.
Schema zur Multiskalenzerlegung (Dekomposition und Rekonstruktion eines Signals – Teilbandzerlegung mit exakter Rekonstruktion)
Dabei stehen H und
Für jede orthonormale Basis aus Wavelets mit kompaktem Träger existieren assoziierte Paare endlicher Filter zur Teilbandzerlegung mit exakter Rekonstruktion.
Wavelet-Analyse versus Fourier-Analyse
Mit Hilfe der Fourier-Analyse können Charakteristika einer Funktion untersucht werden, indem die Funktion in mathematisch einfache Komponenten, in diesem Fall Sinus- und Cosinusfunktionen verschiedener Frequenzen und Amplituden, zerlegt wird. Die wohlbekannten trigonometrischen Funktionen sind einfach zu analysieren, prinzipielle Eigenschaften der Funktion selbst können daraus abgeleitet werden. Fourier-Analyse ist natürlicherweise besonders gut geeignet, periodische Phänome zu analysieren.
Schwierig ist es, mit Hilfe der Fourier-Analyse Information über lokale Phänomene, beispielsweise eine Sprungstelle, zu gewinnen. Je schärfer ein Übergang ist, umso mehr Fourierkomponenten sind nötig, um das Verhalten zu beschreiben.
Wavelet-Analyse hingegen arbeitet mit den skalierten und translatierten Versionen eines einzigen Wavelets ψ. Ein mother wavelet ψ mit kompaktem Träger lebt auf einem endlichen Intervall. Eine Sprungstelle einer Funktion kann analysiert werden, indem nur diejenigen Versionen von ψ betrachtet werden, die sie überlappen. Feinere Details können mit entsprechend fein skalierten Versionen von ψ aufgelöst werden. Die lokale Analyse einer Funktion ist mit Hilfe von nur wenigen Basisfunktionen möglich.
Beispiele von Wavelets
Klassische Beispiele sind die Haar- und Walsh-Basis. Meyer-Wavelets und Daubechies-Wavelets haben ebenfalls orthogonale Translate und sind darüberhinaus beliebig glatt, letztere haben kompakten Träger.
Verallgemeinerungen sind Prä-Wavelets (Ortho-gnonalität nur bezgl. verschiedener Skalen), biorthogonale Wavelets und Wavelet-Pakete.
Mehrdimensionale Wavelets erhält man durch Tensorprodukte oder direkt aus mehrdimensionalen Skalierungsfunktionen (z. B. Boxsplines).
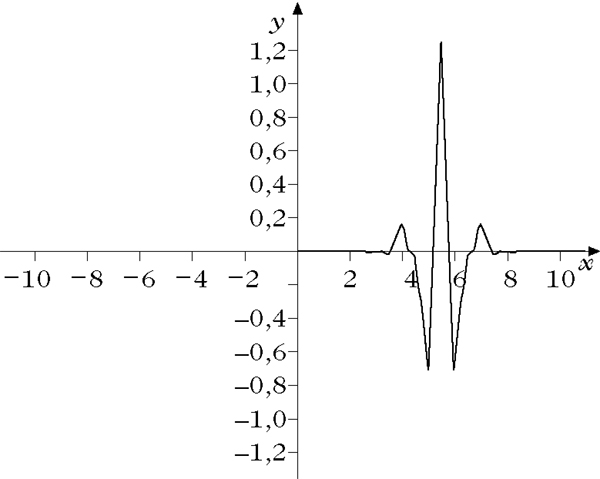
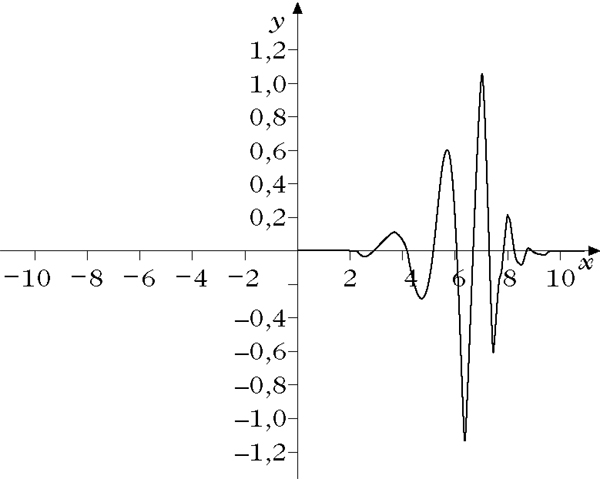
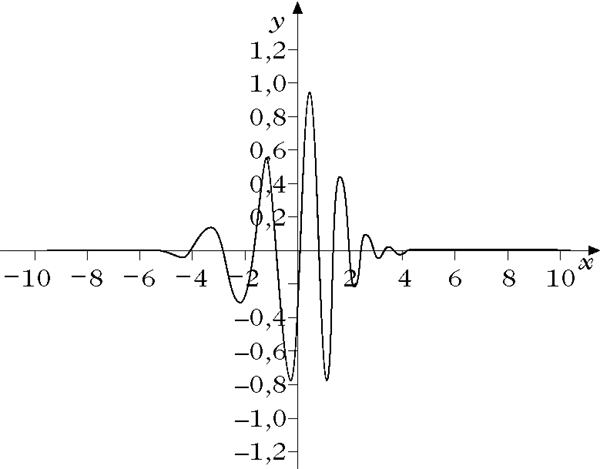
Biorthogonales Wavelet
Daubechies-Wavelet
Differentialoperator-angepaßtes Wavelets
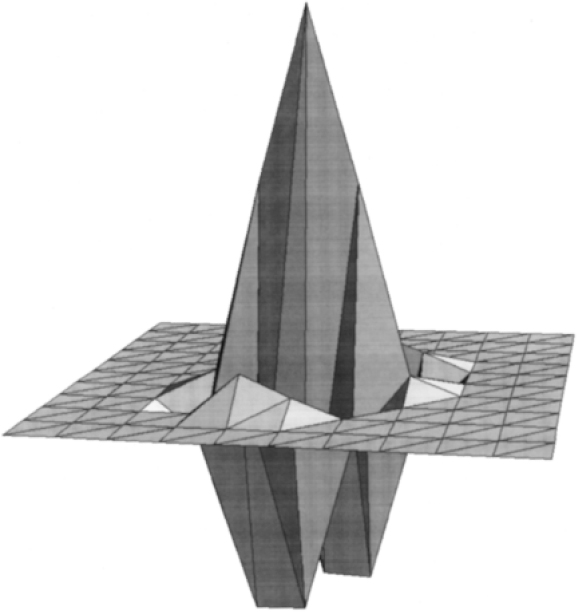
Zweidimensionales Wavelet
Anwendungen
Wichtige Anwendungen von Wavelets finden sich in der Bild- und Signalverarbeitung sowie in der Numerischen Mathematik.
In der Signalanalyse werden Waveletmethoden beispielsweise zur Kompression, Entrauschung oder Kantenerkennung eingesetzt. Typischerweise besteht ein Signal aus einem diskreten Datensatz {λ
Waveletzerlegung eines Signals
Die schnelle Wavelet-Transformation liefert eine nichtredundante Zerlegung des Signals in Grobinformationen λ
In der Numerik bieten Wavelets beispielweise Vorteile bei der Verwendung von Galerkin-Verfah-ren zur Lösung elliptischer partieller Differentialgleichungen. Mit Wavelets lassen sich Basen gerade von denjenigen Funktionenräumen bilden, in denen sich Lösungsfunktionen befinden, zum Beispiel von Sobolewräumen. Sie können daher als Ansatzfunktionen bei Galerkin-Methoden verwendet werden.
Zum einen kann man spezielle an Differentialoperatoren angepaßte Wavelets konstruieren. Sie führen im Galerkin-Verfahren in bestimmten Fällen zu dünn besetzten Steifigkeitsmatrizen mit gleichmäßig beschränkter Konditionszahl. Auch bei allgemeinen linearen Gleichungssystemen, die aus der Diskretisierung elliptischer Differentialgleichungen entstehen und zunächst keine gleichmäßig beschränkte Konditionszahl haben, ist eine Vor-konditionierung mit Hilfe von Wavelets möglich.
Zur numerischen Lösung von Gleichungssystemen mit dünn besetzter Matrix verwendet man gern iterative Verfahren wie zum Beispiel das CG-Verfahren. Die Konvergenz solcher Verfahren hängt häufig von der Konditionszahl der Systemmatrix ab. Eine gleichmäßig beschränkte Konditionszahl ist meist nicht von vornherein gegeben, also ist eine Vorkonditionierung nötig. Diese ist im Wa-veletrahmen unabhängig vom Differentialoperator zu realisieren.
Besondere Stärken von Waveletmethoden ergeben sich auch im Zusammenhang mit adaptiven Verfahren. Ausgehend von der genauen Kenntnis der Basisfunktionen, dem Vorhandensein von verschwindenden Momenten der Wavelets, sowie der Stabilität der entsprechenden Basen können Konvergenzaussagen auch für adaptive Verfahren formuliert werden.
Ein weiteres Anwendungsgebiet von Wavelets in der Numerik ist die Behandlung von Integralgleichungen. Die dabei vorkommenden Systemmatrizen sind in der Regel voll besetzt. Mit Hilfe von Wavelets mit verschwindenden Momenten können die Matrizen ausgedünnt werden, die entsprechenden Gleichungssysteme sind so effizienter zu lösen.
Literatur
[1] Chui, C.K.: An Introduction to Wavelets. Academic Press New York, 1992.
[2] Daubechies, I.: Ten Lectures on Wavelets. SIAM Publishers Philadelpia, 1992.
[3] Louis, A.K.; Maaß, P.; Rieder, A.: Wavelets, Theorie und Anwendungen. Teubner-Verlag Stuttgart, 1998.
[4] Mallat,S.: A Wavelet Tour of Signal Processing. Academic Press New York, 1998.
[5] Meyer, Y.: Ondelettes et Operateurs. Hermann Editeurs des Sciences et des Arts Paris, 1990.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.