Lexikon der Mathematik: Würfeldarstellung einer Booleschen Funktion
Darstellung einer Booleschen Funktion
durch einen markierten n-dimensionalen Würfel 𝔚(f).
Die Knoten des Würfels entsprechen den Elementen des Definitionsbereiches {0, 1}n von f und umgekehrt. Zwei Elemente
die sich an genau einer Stelle unterscheiden, für die also mit einem i ∈ {1..., n} gilt, daß αi ≠ βi und αj = βj ∀j ≠ i ist, sind bezüglich der i-ten Dimension durch eine Kante benachbart.
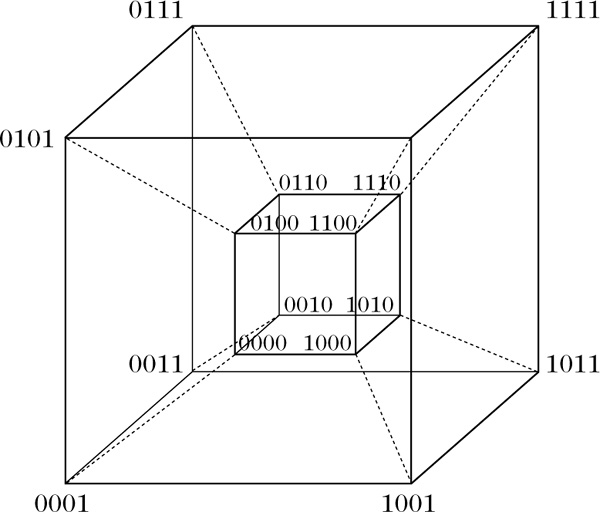
Würfel der Dimension 4
Jeder Knoten v ∈ V, der einem Knoten aus der ON-Menge von f entspricht, wird markiert.
Die Würfeldarstellung wird als anschauliche Darstellung Boolescher Funktionen benutzt, um Minimalpolynome dieser Booleschen Funktionen zu berechnen.
Teilwürfel von 𝔚(f), die nur markierte Knoten enthalten, sind die Implikanten der Booleschen Funktion f. Ein solcher Teilwürfel heißt maximaler Teilwürfel von 𝔚(f), wenn kein Teilwürfel höherer Dimension, der ebenfalls nur markierte Knoten enthält, ihn umfaßt. Maximale Teilwürfel entsprechen den Primimplikanten von f.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.