Lexikon der Mathematik: Zahlengerade
zur Einführung oder Veranschaulichung der reellen Zahlen benutzte Gerade der euklidischen Ebene.
Man wählt dazu etwa eine beliebige Gerade g und legt auf ihr einen Ursprung, der die Null 0 darstellt, und einen davon verschiedenen Punkt zur Darstellung der Eins 1 fest. In der Regel zeichnet man g (bzw. den interessierenden Ausschnitt von g) waagrecht, legt die Eins rechts von der Null und markiert diese und weitere jeweils interessante Zahlen durch kleine senkrechte Striche. Negative reelle Zahlen liegen links von der Null und positive rechts von ihr. Eine positive Zahl x steht an derjenigen Stelle P rechts von 0, an der für die Längen |0P| und |01| der Strecken 0P und 01 gilt: |0P| = x|01|.
Die Addition reeller Zahlen entspricht dem Aneinandersetzen der zugehörigen Strecken der Zahlengeraden (unter Beachtung der Richtung) und die Multiplikation einer Streckung. Die Ordnungsrelation ≤ von R wird durch die Relation ‚liegt links von‘ wiedergegeben. In der Tat lassen sich mit Hilfe der Zahlengeraden vor allem Ordnungsverhältnisse von Zahlen gut darstellen, beispielsweise um die Eigenschaften monotoner Folgen zu veranschaulichen.
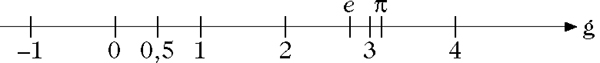
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.