Partition der Eins, Teilung der Eins, endliches Funktionensystem, für welches ein linearer Operator definiert ist, der Konstanten reproduziert.

Es seien C[a, b] die Menge der reellwertigen stetigen Funktionen auf [a, b], G ein (n + 1)-dimensionaler Teilraum von C[a, b] und {g₀, …, g_n} eine Basis von G. Falls ein linearer Operator H : G[a, b] ↦ G, \begin{eqnarray}H(f)=\displaystyle \sum _{j=0}^{n}{\lambda}_{j}(f){g}_{j},\end{eqnarray} mit der Eigenschaft H(1) = 1 existiert, so bildet {g₀, …, g_n} hinsichtlich H eine Zerlegung der Eins.

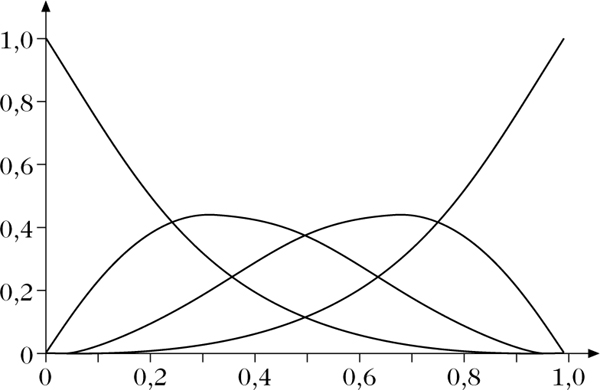
Ein Beispiel für eine Zerlegung der Eins ist gegeben durch die Bernstein-Polynome \begin{eqnarray}{B}_{j}^{n}(x)=\left(\begin{array}{c}n\\j\end{array}\right){x}^{j}(1-x)^{n-j},\,j=0,\ldots,n,\,x\in [0,1],\end{eqnarray} denn es gilt nach dem binomischen Lehrsatz \begin{eqnarray}\displaystyle \sum _{j=0}^{n}{B}_{j}^{n}(x)=1,\,\,\,x\in [0,1].\end{eqnarray} In diesem Fall ist G der Raum der Polynome vom maximalen Grad n, und \begin{eqnarray}H(f)=\displaystyle \sum _{j=0}^{n}f\left(\frac{j}{n}\right){B}_{j}^{n}\end{eqnarray} der Bernstein-Operator, welcher auch im Zusammenhang mit dem Satz von Korowkin auftritt.

Normalisierte B-Splines haben ebenfalls die Eigenschaft, eine Zerlegung der Eins zu bilden.

Die Eigenschaft der Zerlegung der Eins stellt in der Approximationstheorie eine Minimalforderung an ein Funktionensystem G (und den zugehörigen Operator H) dar. Dort ist man im allgemeinen bestrebt, für ein geeignetes Funktionensystem Operatoren so zu konstruieren, daß Polynome möglichst hohen Grades reproduziert werden, denn dadurch verbessert sich im allgemeinen deren Approximationsverhalten.

Zerlegungen der Eins können auch in offensichtlicher Weise für multivariate Funktionensysteme definiert werden.