Lexikon der Mathematik: Zerlegung einer affinen Hyperfläche
Darstellung einer Hyperfläche als Vereinigung von irreduziblen Hyperflächen.
Zerlegung einer Kurve© Springer-Verlag GmbH Deutschland 2017 Bild vergrößern
Wenn die Hyperfläche H durch die Gleichung f = 0 definiert ist,
Copyright Springer Verlag GmbH Deutschland 2017
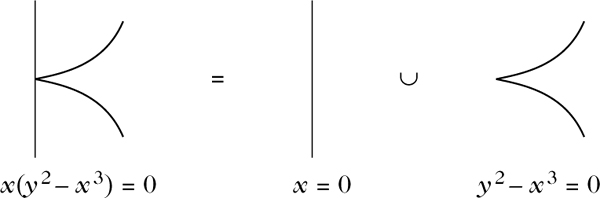
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.