spezielle Koordinaten im ℝ³.

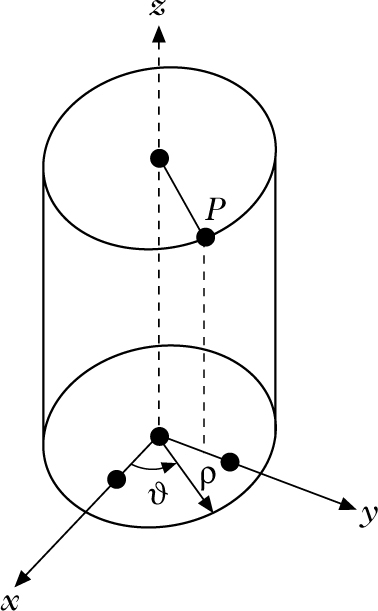
Zylinderkoordinaten bestehen aus den Polarkoordinaten (ϱ, ϑ) der Projektion eines Punktes P auf die (x, y)-Ebene und der Applikate z (orientierter Abstand des Punktes von der (x, y)-Ebene). ϱ ist der Zylinderradius (Abstand des Punktes von der z-Achse), ϑ der Winkel zwischen der positiven x-Achse und der Projektion der Strecke \(\overline{\text{OP}}\) auf die (x, y)-Ebene: \begin{eqnarray}\Phi :[0,\infty )\times [0,2\pi )\times {\mathbb{R}}\,{\unicode {8717}}\,\left(\begin{array}{c}\varrho \\ \vartheta \\ z\end{array}\right)\mapsto \left(\begin{array}{c}\varrho \cos \vartheta \\ \varrho \sin \vartheta \\ z\end{array}\right)\in {{\mathbb{R}}}^{3}\end{eqnarray}

Φ ist surjektiv und stetig differenzierbar mit \begin{eqnarray}\det {\Phi }{^{\prime} }\left(\begin{array}{l}\varrho \\ \vartheta \\ z\end{array}\right)=\varrho.\end{eqnarray}

Zylinderkoordinaten sind hilfreich bei dreidimensionalen Fragestellungen mit Rotationssymmetrie bzgl. der z-Achse.