Selbstorganisationw,Eself-organization, Bezeichnung für verschiedene Phänomene von spontaner Strukturbildung in nichtlinearen dynamischen Systemen (Nichtlinearität). Solche Beispiele für die durch Selbstorganisation entstehenden zeitlich, räumlich oder funktional geordneten Strukturen sind in vielen Bereichen der Physik, Chemie, Technik und Biologie zu finden ( siehe Zusatzinfo ). Attraktor, Autopoiese, dissipative Strukturen, Prigogine, Synergetik.

Die Erforschung komplexer Systeme ist mit herkömmlichen reduktionistischen mathematisch-physikalischen Methoden nur eingeschränkt möglich. Damit sind auch der globalen, quantitativen Beschreibung von Gehirnaktivitäten enge Grenzen gesetzt. Im Rahmen von Chaostheorie und Synergetik lassen sich jedoch die Wechselwirkungen zwischen einer großen Anzahl von Nervenzellen untereinander und mit Bezug auf Sinnesreize und Verhaltensweisen gleichsam "von oben her" erforschen. Während die reduktionistischen Ansätze Eigenschaften, Funktionen und Leistungen höherer Betrachtungsebenen auf möglichst tiefe (mikroskopische) Ebenen zurückführen und sogar daraus ableiten wollen (E bottom up approach), also etwa die makroskopische Dynamik der Hirnaktivitäten, das Verhalten oder unser geistiges Erleben durch die Eigenschaften von Neuronen und die Verschaltungen bestimmter Nervennetze erklären möchten, versuchen die holistischen Ansätze zunächst einmal Gesetzmäßigkeiten der höheren Betrachtungsebenen zu finden und von diesen aus auf zugrundeliegende Mechanismen zu schließen (E top down approach). Aufgrund der Komplexität der Wechselwirkung zwischen den Strukturen dieser tieferen Systemebenen und den nur ungenau bekannten Randbedingungen lassen sich die daraus hervorgehenden Eigenschaften und Prozesse nicht oder nur unvollständig herleiten. Sie sind emergent, also epistemisch nicht reduzierbar (woraus aber nicht folgt, daß sie ontologisch irreduzibel sind, d.h. außerhalb der physikalischen Welt stehen). Eine einzelne Nervenzelle z.B. riecht, sieht und fühlt nicht, ebenso sind einzelne Wassermoleküle nicht flüssig und durchsichtig. Insofern ist das Ganze mehr als die Summe seiner Teile und erfordert eine eigene Betrachtungsweise ( siehe Tab. ). Solche holistischen, naturwissenschaftlichen Forschungsansätze haben gemeinsam, daß sie das Gehirn als ein komplexes offenes System ansehen. Offen meint hier, daß es über die Sinnesorgane und Muskeln (und natürlich auch die Gliazellen, Blutgefäße usw.) mit seiner Umwelt in einem regen und komplizierten stofflichen und energetischen Austausch steht. Die von den externen und internen Reizen ausgelösten und zu motorischen Aktivitäten führenden räumlichen und zeitlichen Erregungsmuster im Cortex lassen sich unmöglich in allen Details verfolgen und analysieren. Man müßte dazu nicht nur das Gehirn vollständig beschreiben und berechnen können, sondern auch noch seine Umwelt, die mit ihm interagiert. Verschiedene Verfahren wie die Positronenemissionstomographie (PET), funktionelle Kernspinresonanztomographie (fMRI), Elektroencephalographie (EEG) und Magnetoencephalographie (MEG) erlauben es aber, das menschliche Gehirn und seine Prozesse näherungsweise und global zu untersuchen, ohne daß der Schädel geöffnet werden muß. Die beiden letztgenannten Methoden sind gegenwärtig die einzigen nichtinvasiven, die eine quantitative und kontinuierliche, quasi zeitgleiche Verfolgung der Hirnprozesse erlauben. Die kleinsten Änderungen der von den Nervenzellen der Großhirnrinde produzierten elektrischen bzw. magnetischen Felder geben Auskunft sowohl über die corticalen Eigenaktivitäten und generellen Zustände (Wachen, Schlafen, Träumen) als auch über Reaktionen (evozierte Potentiale) auf äußere Reize, etwa Töne oder Bilder. Diese Felder stammen freilich von den Aktivitäten einer enormen Anzahl von Nervenzellen – eine einzelne extracraniale Elektrode summiert über die synaptischen Potentiale von schätzungsweise 10 bis 1000 Millionen Nervenzellen. Die Felder sind also relativ großräumige Eigenschaften des Cortex. Inwiefern sie eher als Beiprodukte denn als Ursachen in den Kausalketten angesehen werden müssen – vergleichbar dem Verkehrslärm von einer unterschiedlich stark befahrenen Straße, der die Verkehrssituation anzeigt, aber praktisch nicht beeinflußt –, oder ob und welche Auswirkungen sie haben, läßt sich bislang kaum sagen. Doch selbst aus der Analyse des "Verkehrslärms" kann man vieles lernen und rückschließen. Die globalen Messungen der Hirnaktivitäten erlauben nun neuerdings – über bloße Aussagen von Korrelationen bestimmter Hirnprozesse mit Verhalten und kognitiven Leistungen hinaus – Einsichten in die Dynamik der neuronalen Verarbeitungen sensorischer Inputs und motorischer Outputs (Zeit und Gehirn).
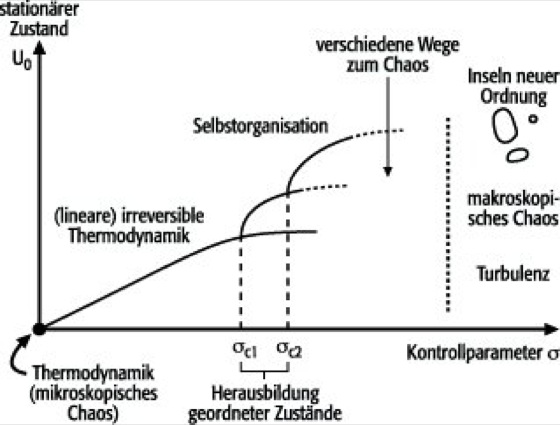
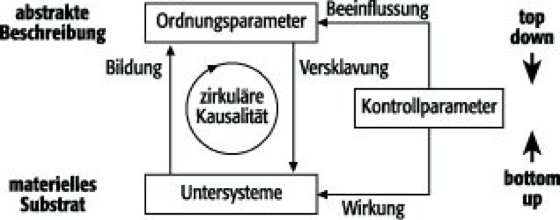
Selbstorganisation und Chaos: Bei Betrachtung dieser Zusammenhänge sind besonders physikalische und mathematische Methoden fruchtbar, die für das Verständnis komplexer Systeme entwickelt worden sind und oft unter dem Schlagwort Selbstorganisation firmieren (auch das Phänomen, das sie behandeln, wird so genannt). Sie beschreiben Systeme, die aus einer Vielzahl von Elementen bestehen, welche auf bestimmte Weise miteinander wechselwirken, und machen Aussagen über die äußeren Bedingungen eines solchen Systems, die in Form unspezifischer Kontrollparameter formuliert werden ( siehe Abb. 1 ). Diese repräsentieren z.B. den Fluß von Energie oder Materie durch das System. Aufgrund des nicht näher spezifizierten Charakters der mikroskopischen Elemente ist das Anwendungsfeld dieser mathematischen Strukturtheorien ziemlich weit. In der Abbildung ist der stationäre Zustand U₀ über einem Kontrollparameter σ aufgetragen, der den Abstand zum thermischen Gleichgewicht messen soll. Unter dem stationären Zustand eines Systems wird der makroskopische Zustand verstanden, den es nach einer gewissen Einschwingzeit (Relaxationszeit) einnimmt und der sich bei gleichbleibenden Randbedingungen nicht ändert. Ist z.B. bei einer mit Wasser gefüllten Badewanne die Wasseroberfläche zur Ruhe gekommen, so hat diese einen makroskopisch stationären Zustand eingenommen, obwohl die einzelnen Wassermoleküle nach wie vor eine wilde Bewegung ausführen (mikroskopisches Chaos). Dieses System befindet sich im thermischen Gleichgewicht, solange keine äußeren Einflüsse einwirken, etwa ein erneuter Wasserzufluß oder eine Hand, die das Wasser bewegt. Dieser Gleichgewichtszustand entspricht dem Ursprung des Achsenkreuzes in Abb. 1 und wird von der Thermodynamik beschrieben. Treibt man das System nun aus dem thermodynamischen Gleichgewicht, so bedeutet das eine Veränderung des Kontrollparameters. Dies entspricht z.B. einem konstanten Zu- und Abfluß in die bzw. aus der Badewanne. Dieser Bereich wird von der (linearen) irreversiblen Nichtgleichgewichtsthermodynamik beschrieben, für deren Formulierung Ilya Prigogine 1977 den Nobelpreis erhielt. Entfernt man sich noch weiter vom thermodynamischen Gleichgewicht, so setzt am Punkt σ_c, wenn der thermodynamische Zustand instabil wird, der Zuständigkeitsbereich der Synergetik ein. Diese "Lehre vom Zusammenwirken" wurde in den 1970er Jahren von Hermann Haken entwickelt. An kritischen Werten eines Kontrollparameters bricht die bestehende makroskopische Ordnung zusammen, und es entsteht durch Selbstorganisation ein neuer Ordnungszustand. Im Falle der Gehirnaktivitäten sind solche Kontrollparameter z.B. die Einnahme von Drogen oder Anästhetika, die die makroskopischen Gehirnzustände und entsprechend die Verhaltensmuster eines Menschen zu ändern vermögen. Ebenso können auch optische oder akustische Reize als Kontrollparameter dienen. Haken zeigte, daß im Bereich kritischer Werte des Kontrollparameters, an sogenannten Phasenübergangspunkten, die Dynamik des gesamten Systems durch wenige Variablen dominiert ("versklavt") wird, den sogenannten Ordnungsparametern ( siehe Abb. 2 ). Auf diese Weise kommt es in der mathematischen Beschreibung zu einer enormen Verringerung der Anzahl an relevanten Variablen, da die makroskopische Dynamik durch die Evolutionsgleichungen dieser wenigen Ordnungsparameter determiniert ist. Diese Informationsreduktion erlaubt es, qualitative Änderungen in vielen komplexen Systemen noch mathematisch zu erfassen. Die Methoden der Synergetik finden Anwendung in unterschiedlichen Wissensbereichen wie der Physik, Chemie, Biologie, Ökonomie oder Soziologie. Dort stellen die mikroskopischen Elemente beispielsweise Gasmoleküle, Individuen einer Population, Betriebe eines Wirtschaftszweigs oder Mitglieder einer Volksgruppe dar. Wächst der Kontrollparameter σ noch weiter an, können sich an dessen kritischen Werten die makroskopischen Zustände erneut ändern, bis schließlich der Bereich des deterministischen Chaos erreicht wird. Solche Systeme sind zwar im Prinzip mathematisch vollständig determiniert, doch ihre Dynamik läßt sich nur für sehr kleine Zeiten vorhersagen. Dies liegt an der hohen Empfindlichkeit der Prozesse gegenüber den Anfangsbedingungen. Das bedeutet, daß bei Wiederholung eines Experiments oder einer Berechnung eine winzige Abweichung in den Anfangsbedingungen bereits eine völlig unterschiedliche Dynamik zur Folge hat. So können auch kleine Ursachen große Wirkungen entfalten. In solchen Systemen herrscht (mathematisch wohldefiniertes) makroskopisches Chaos. Jedoch können auch dort Inseln stabiler neuer Ordnung auftreten, die im Normalfall auf kleine Parameterbereiche beschränkt sind. Bei weiterer Erhöhung des Kontrollparameters bildet vermutlich die voll entwickelte Turbulenz das Ende dieser Kette ( siehe Abb. 1 ).
Erforschung raumzeitlicher Strukturen im Gehirn: Raumzeitliche Strukturen sind räumliche Muster, die sich mit der Zeit verändern. Ein Beispiel dafür sind die Bewegungen der Wellenmuster an einer Wasseroberfläche, die Wellentäler und -berge. Wird am Gehirn ein EEG oder MEG aufgenommen, welches Signale von mehreren Sensoren erhält, die am Kopf räumlich verteilt sind, so bilden die gemessenen elektrischen oder magnetischen Feldstärken ebenfalls ein raumzeitliches Signal. Liefern die Sensoren kein wildes Durcheinander an Signalen, sondern läßt sich eine gewisse Ordnung in Raum und Zeit feststellen, so spricht man von kohärenten raumzeitlichen Strukturen. Sie stellen die makroskopische Ebene dar. Ein Sensor mißt im allgemeinen Signale, die von Millionen von Neuronen verursacht werden. Die Nervenzellen und ihre einzelnen Aktivitäten entsprechen der mikroskopischen Ebene. Bemerkenswert ist, daß Chaos nicht notwendigerweise fatale Folgen hat, wie die Umgangssprache suggerieren mag. Die EEG-Muster von gesunden, wachen Menschen sind scheinbar wirr und unvorhersagbar, während die Kurven bei einem epileptischen Anfall erstaunlich regelmäßig aussehen. Und weiter zeigte sich, daß im entspannten Zustand (Alpha-Wellen) die Muster unvorhersagbar erscheinen, also wohl chaotischen oder statistischen Charakter haben, aber mit nur wenigen Ordnungsparametern beschrieben werden können. Die Synergetik interpretiert solche Eigenschaften als Manifestationen von Selbstorganisationsprozessen. Da das Gehirn eine enorme Flexibilität und rasche Anpassungsfähigkeit in seinem Verhalten aufweist, scheint sich seine Dynamik in der Nähe von Instabilitätspunkten abzuspielen, einem kritischen Bereich, wo Phasenübergänge von einem makroskopischen Zustand zu einem anderen stattfinden können. Treten solche Übergänge dann auf, zeigen die EEG- und MEG-Aufzeichnungen tatsächlich die Vorherrschaft nur noch weniger Ordnungsparameter und damit spezifischer, stabiler Prozesse von größerem Ordnungsgrad an. Die komplexen, oft regelrecht verwirrenden EEG- und MEG-Muster lassen sich dabei als Überlagerung der einzelnen grundlegenden Ordnungsparameter modellieren. Sogar die fraktale Dimension und somit die Chaotizität der einzelnen Muster kann abgeschätzt werden. Auch das Bereitschaftspotential vor einer Handlung kann als Folge von Selbstorganisationsprozessen aufgefaßt werden. – Es sind mehrere Zugänge entwickelt worden, die versuchen, ein Verständnis der Dynamik der raumzeitlichen Strukturen im Gehirn zu erlangen.
1) Paul Nuñez untersuchte, welche Symmetrien einer solchen raumzeitlichen Dynamik im Gehirn zugrundeliegen können. Eine Kugel kann z.B. an jeder beliebigen Fläche, die durch den Kugelmittelpunkt führt, gespiegelt werden. Bei einem Würfel ist dies nicht der Fall. Systeme verschiedenartiger Symmetrie entwickeln topologisch unterschiedliche räumliche Strukturen. Nun hat die menschliche Großhirnrinde eine überaus komplizierte Architektur. Die von Nuñez erforschten Symmetrien raumzeitlicher EEG-Muster stellen effektive oder resultierende Symmetrien dar, die die Grundlage der Dynamik dieser Strukturen bilden, aber in erster Linie nicht unbedingt mit physiologischen Strukturen übereinstimmen müssen. Ausgehend von einer Masse neuronalen Gewebes entwickelte Nuñez einen Satz von mathematischen linearen Modellgleichungen, welche die Aktivität des Nervengewebes abhängig von Raum und Zeit beschreiben. Diese Gleichungen werden bei Nuñez unter der Symmetrie eines Ringes und der Kugelsymmetrie diskutiert, welche sich als pragmatische Beschreibung erwiesen haben. Die Besonderheit der Arbeiten von Nuñez liegt darin, daß er die Parameter in seinen Modellen physiologisch meßbaren Daten anpaßt und dann Vorhersagen zu treffen vermag, etwa über Frequenzbereiche, in denen bestimmte raumzeitliche Muster auftreten können. Diese stimmen gut mit experimentellen EEG-Daten überein. Der Nachteil dieses Zugangs ist jedoch, daß die Linearität seiner Modellgleichungen eine grobe Näherung darstellt, die nur eine sehr eingeschränkte Gültigkeit hat.
2) Walter Freeman vollzog den Schritt in den nichtlinearen Bereich. Er hat sowohl experimentell als auch theoretisch die raumzeitliche Dynamik im Bulbus olfactorius von Kaninchengehirnen nach Inhalation von Geruchsstoffen untersucht, die diese Cortexbereiche stimulieren. Hierbei maß er das EEG und erhielt Raum-Zeit-Strukturen, die er als chaotisch identifizieren konnte. Meist handelt es sich um elektrische Salven mit Frequenzen um 40 Hz, die sich über den ganzen Riechkolben ausbreiten. Zur mathematischen Beschreibung der EEG-Muster entwarf Freeman Modelle, die auf einem Satz nichtlinear gekoppelter Differentialgleichungen basieren und einen sogenannten Attraktor der experimentell beobachteten Dynamik näherungsweise reproduzieren können. Ein Attraktor ist ein stabiler, stationärer Zustand eines im Austausch mit der Umwelt stehenden Systems, der, einmal erreicht, vom System nicht selbst wieder verlassen werden kann. Auch nach einer kurzfristigen, nicht zu großen externen Störung, die das System aus dem Attraktorzustand auslenkt, kehrt es wieder in diesen zurück (Relaxation). Chaotische Attraktoren bezeichnet man als seltsame Attraktoren(Estrange attractors). Solche seltsamen Attraktoren glaubt Freeman in den EEGs zu finden; sie könnten mit dem Gedächtnis der Düfte und ihrer Wiedererkennung zusammenhängen und dürften durch neue Erfahrungen abgewandelt werden. Durch die wechselseitige Erregung mindestens zweier Hirnareale, einem neuronalen "Tauziehen", das nicht zur Ruhe kommen oder sich auf eine gemeinsame Frequenz einigen kann, und das immer neue Aktivitäten des Organismus auslöst, kommt Freeman zufolge die chaotische Dynamik zustande – nicht als Nebenprodukt, sondern als wesentliche Eigenschaft komplexer Nervenzellverbände. Die Problematik der Erforschung einer solchen Dynamik besteht freilich darin, daß eine chaotische Zeitserie infolge der Sensitivität gegenüber den Anfangs- und Randbedingungen nie über eine längere Zeitspanne hinweg reproduziert werden kann. Nur die Attraktoren sind reproduzierbar. Die Fragen, welcher Attraktor die beobachtete Dynamik beschreibt, welche fraktale Dimensionalität er hat usw., sind aber nur sehr schwer zu beantworten.
3) Einen leichteren Zugang ermöglicht die Untersuchung von Phänomenen, die mit sogenannten Grenzzyklusattraktoren (Grenzzyklus) charakterisiert werden können. Sie beschreiben eine Dynamik, die sich nach einer spezifischen Einschwingzeit durch periodische Bewegungen darstellen läßt. Diesen methodischen Zugang haben Hermann Haken und Scott Kelso gewählt. Sie fassen das Gehirn als offenes, komplexes, sich selbstorganisierendes System auf, das in der Nähe von Instabilitätspunkten arbeitet. Dieser Ansatz ermöglicht ein enormes Maß an Flexibilität und Adaptabilität. Die Phasenübergänge können dabei vielgestaltig sein. Sie lassen sich z.B. als Übergang von einem Grenzzyklus zu einem chaotischen Attraktor oder zu einem anderen Grenzzyklusattraktor auffassen. Die Synergetik kann somit auch Beiträge für die Hirnforschung und Wahrnehmungspsychologie liefern.
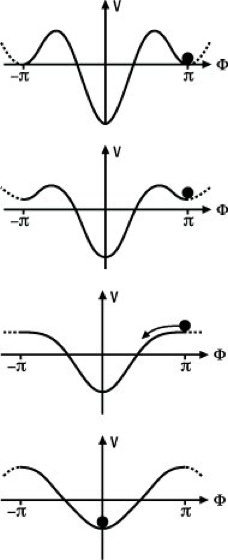
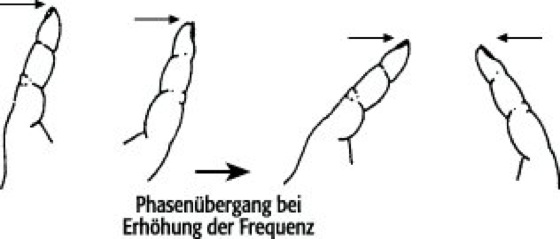
Koordinationsexperimente verdeutlichen die Methoden und Erfolge synergetischer Beschreibungen besonders gut. Das erste Experiment ist ein motorisches Koordinationsexperiment, in welchem eine Versuchsperson ihre beiden Zeigefinger gegenphasig zueinander hin und her bewegt ( siehe Abb. 3 ). Da die Hände spiegelsymmetrisch zueinander sind, bedeutet Gegenphase für den linken Zeigefinger eine Bewegung nach links, wenn der rechte Zeigefinger sich ebenfalls nach links bewegt. Erhöht man die Fingerbewegungsfrequenz, so findet bei einer kritischen Frequenz ein unwillkürlicher Übergang von Gegenphase in Gleichphase statt. Dieser Übergang ist spontan und läßt sich nicht verhindern. Er scheint eine spezifische Charakteristik des menschlichen motorischen Systems zu sein. Wird umgekehrt mit gleichphasigen Bewegungen begonnen, findet jedoch kein Übergang in Gegenphase statt. Vor dem Übergang liegen also zwei mögliche Zustände vor: Gleichphase und Gegenphase, nach dem Übergang nur noch der Zustand der Gleichphase. Zur mathematischen Beschreibung dieser Beobachtungen siehe Abb. 4 . Die schwarze Kugel repräsentiert den momentanen Zustand der Bewegung. Die äußere Mulde stellt den gegenphasigen Zustand dar, die innere den gleichphasigen. Bei Erhöhung der Bewegungsfrequenz wird die äußere Mulde flacher, bis man an die kritische Frequenz gelangt. Dort kann sich die Kugel dann nicht mehr halten und rollt in die innere tiefere Mulde hinab, welche dem gleichphasigen Bewegungszustand entspricht. Ist die Kugel dort einmal angelangt, kommt sie aus dieser Senke nicht mehr heraus, selbst wenn die Bewegungsfrequenz wieder erniedrigt wird. Diese Darstellung wurde von Haken, Kelso und Herbert Bunz vorgeschlagen. Sie modellierten die Dynamik der Zeigefinger mathematisch durch zwei Oszillatoren, die nichtlinear gekoppelt sind und bei der kritischen Frequenz diesen in Abb. 4 illustrierten Phasenübergang ausführen. Der in diesem Modell verwendete Kopplungsmechanismus ist als HKB-Kopplung bekannt geworden. Mit dem Modell läßt sich auch erklären, daß bei einem Start oberhalb der kritischen Frequenz nur gleichphasige Bewegung möglich ist und kein Übergang in den gegenphasigen Zustand stattfindet, wenn die Frequenz der Fingerbewegungen dann erniedrigt wird. Dies konnte experimentell leicht bestätigt werden. Es liegt eine sogenannte Hysterese (Beharrung in einem Zustand) vor – die Kugel im Diagramm kann die zentrale Mulde nicht verlassen. In einem zweiten Experiment fand unter analogen Bedingungen eine Koordination zwischen Fingerbewegung und einem akustischen äußeren Stimulus statt: Jeweils zwischen zwei Pfeiftönen mußte die Versuchsperson eine Taste drücken. Der zeitliche Abstand der Töne wurde nach und nach vermindert. Entsprechend trat bei einer kritischen Stimulusfrequenz ein unwillkürlicher Übergang von gegenphasiger Koordination zu gleichphasiger Koordination zwischen Fingerbewegung und akustischem Stimulus auf; die Tastendrücke erfolgten nun nicht mehr zwischen, sondern mit den Pfeiftönen. (Ein solches Phänomen ist auch vom Applaus des Publikums nach einem Konzert oder Theaterstück bekannt: Von einem ungeordneten Klatschen geht der Beifall spontan in ein geordnetes gleichphasiges Klatschen über, welchem man sich schwer entziehen kann.) Dieser Übergang läßt sich mit Hilfe der HKB-Kopplung mathematisch beschreiben: Die Bewegung eines Zeigefingers wird mit dem äußeren akustischen Stimulus identifiziert. Ansonsten wird das Modell aus dem ersten Experiment beibehalten. Eine mathematische Diskussion der erhaltenen Gleichungen zeigt, daß die experimentell beobachteten Phänomene mit diesen modifizierten Gleichungen reproduziert werden können. Dasselbe Phänomen wurde auch bei Experimenten mit einer visuellen Kopplung zweier Personen gefunden. Deren Aufgabe war es, ein Pendel oder das eigene Bein in Gegenphase zum Pendel bzw. Bein der anderen Person zu bewegen. Es trat wiederum bei einer kritischen Frequenz ein Übergang in den gleichphasigen Bewegungszustand auf. Bei einem dritten Experiment wurde während des zweiten Experiments (Finger – Stimulus) bei der Versuchsperson ein MEG aufgenommen. Die Datenanalyse zeigte, daß hier kohärente makroskopische Raum-Zeit-Strukturen im Gehirn entstehen und einen Phasenübergang bei derselben kritischen Stimulusfrequenz aufweisen, bei der auch der Phasenübergang im motorischen Verhalten auftritt. Und wiederum kann dieser Übergang mathematisch beschrieben werden, indem in der HKB-Kopplung der eine Zeigefinger durch den äußeren akustischen Stimulus und der andere Zeigefinger durch das raumzeitliche Gehirnsignal ersetzt wird. Dies legt die Hypothese nahe, daß die HKB-Kopplung einen Kopplungsmechanismus des Nervensystems beschreibt, der für Koordinationen maßgeblich ist. (Tatsächlich konnten auf diese Weise z.B. auch die veränderten Gangarten von Pferden beim Übergang vom Schritt in Trab und vom Trab in den Galopp modelliert werden.) Derselbe Kopplungsmechanismus ist also sowohl in Fällen von Interaktion körperinterner Vorgänge untereinander als auch körperinterner und -externer Vorgänge miteinander wirksam. Er zeigt, daß die neuronal gesteuerte Motorik nicht einfach mit einem klassischen Computerprogramm gleichgesetzt werden kann, denn dies hat weder Platz für zufällige Schwankungen, wie sie beim Phasenübergang beobachtet werden, noch zeigt es Phänomene wie die Hysterese und das sogenannte kritische Langsamerwerden.
Die Erforschung komplexer Systeme: Selbstorganisationstheorien wie Chaostheorie und Synergetik eröffnen also einen neuen Zugang zu den makroskopischen, komplexen Erregungsmustern des Gehirns und deren Interaktion mit seiner Umwelt. Dabei ist es möglich, von den einzelnen Verschaltungen und elektrochemischen Prozessen großer Nervenzellverbände abzusehen und sich allein auf bestimmte Gesamteigenschaften ganzer, als Black-box (Black-box-Verfahren) behandelbarer Neuronenmassen zu beschränken, deren raumzeitliche Dynamik in gesetzmäßiger Weise von speziellen Randbedingungen und Wechselwirkungen mit anderen Systemen abhängt. Inwiefern solchen globalen, in der Synergetik z.B. als Ordnungsparameter bezeichneten und mathematisch formulierbaren Größen zur Beschreibung dieser Dynamik eine eigenständige, etwa mit den elektrischen Eigenschaften von Nervenzellen vergleichbare Realität zukommt oder ob bzw. an welcher Stelle sie nur Metaphern ohne kausale Relevanz sind, ist eine interessante und kontrovers diskutierte Frage. Faßt man Selbstorganisationstheorien in erster Linie als Strukturtheorien auf, lassen sich diese Größen als bestimmte, Theorie-abhängig ausgewählte Abstraktionen ansehen, die sich unabhängig von der Frage nach ihrem ontologischen Status praktisch bewähren ( siehe Zusatzinfo ). – Das Selbstorganisations-Paradigma bleibt keineswegs auf physikalische, chemische und biologische Fragestellungen beschränkt. Auch psychologische Phänomene wie Wahrnehmungsambiguitäten (Kippfigur) einschließlich des binokularen Wettstreits sowie Figur-Hintergrund-Erkennen und sogar bewußte Entscheidungsprozesse können als Symmetriebrüche und damit Selbstorganisationsvorgänge aufgefaßt werden. Mustererkennung läßt sich damit in der Synergetik analog zur Musterbildung beschreiben. Wenn ein Ordnungsparameter den Wettbewerb zwischen verschiedenen Ordnern gewonnen hat, versklavt er gleichsam das ganze System (in der mathematischen Beschreibung wird ein Minimum in der vieldimensionalen Funktionenlandschaft erreicht) und prägt dem Gehirn einen vorübergehenden Endzustand auf: ein Objekt wird erkannt. Im Rahmen des synergetischen Computers wurde es möglich, Musterbildung und Mustererkennung als zwei Seiten derselben Medaille zu beschreiben und damit nicht nur Mechanismen der Wahrnehmung, sondern auch der Gedächtnisbildung und des Erinnerns zu simulieren (Lernen). Einmal gelernte Gesichter z.B. kann der Computer auch in verrauschtem Zustand oder unter einem Gewirr anderer Gesichter reidentifizieren. Einem bestimmten Gesicht bzw. simulierten neuronalen Aktivitätsmuster entspricht dabei ein bestimmter Ordnungsparameter, und bei doppeldeutigen Figuren kommt es zu einem Wettbewerb dieser Ordner. Mit Hilfe eines Aufmerksamkeitsparameters kann auch das "Kippen" bei der Wahrnehmung doppeldeutiger Figuren modelliert werden. Im Gegensatz zu den klassischen künstlichen neuronalen Netzen, bei denen die Veränderungen in den synaptischen Gewichtungen nicht im einzelnen nachvollzogen werden können, lassen sich die mikroskopischen Prozesse im synergetischen Computer viel detaillierter verstehen und z.B. auch im Rahmen einer Lerntheorie (über Prototypen) verstehen. Auch kann den Aktivitätsmustern wegen der zugrundeliegenden Ordner eine Bedeutung zugeordnet werden. Motorisches Lernen läßt sich synergetisch ebenfalls beschreiben: als eine Veränderung der Ordnungsparameter. Dies geschieht aber nicht durch Ersetzung eines Ordners, sondern durch die Überlagerung eines zweiten, so daß zwar der Einfluß des neuen Parameters zunehmend stärker wird, aber vom ursprünglichen Ordner immer noch etwas erhalten bleibt. Das steht mit der Beobachtung im Einklang, daß beim Lernen neuer Bewegungsformen immer wieder einmal die früheren "durchschlagen". – Mit einigem Erfolg ist es in der Synergetik überdies gelungen, konzeptuell und in Ansätzen sogar quantitativ bestimmte soziologische und ökonomische Aspekte zu modellieren, etwa Phasenübergänge in der Politik (Revolutionen) und Wirtschaft (Börsencrashs) oder die Entwicklung von Dialekten (Sprache), Verkehrsstaus, Städten und Völkerwanderungen. Entsprechend könnten abstrakte Begriffe wie Moral, Nationalgefühl oder Zeitgeist als Ordnungsparameter unseres Denkens wirken. Sie werden durch unser Denken hervorgebracht, doch ebenso bestimmen sie unser Denken auch. Vielleicht lassen sich alle geistigen Vorgänge als emergent im Licht einer Selbstorganisation der Materie deuten (Leib-Seele-Problem, Willensfreiheit). Beispielsweise könnte in der chaotischen Dynamik des Cortex ein Spezifikum (und eine notwendige Bedingung) für Denken und Bewußtsein liegen, der etwa von den gegenwärtigen Versuchen, künstliche Intelligenz zu erzeugen, kaum Rechnung getragen wird. Möglicherweise lassen sich Gedanken mit Ordnungsparametern gleichsetzen. Sie würden also vom Nervensystem hervorgebracht, aber über rückgekoppelte Kausalität auf dieses zurückwirken. Insofern wären psychische Ereignisse in dem vagen Sinn der Begriffe materiell und naturalistisch fundiert, aber auch eigengesetzlich und epistemisch nicht einfach auf physische Ereignisse reduzierbar. Auch die Grundidee der multiplen Realisierbarkeit steht mit den Selbstorganisationstheorien im Einklang: Komplexe Systeme aus unterschiedlichen materiellen Bestandteilen können bei geeigneten Wechselwirkungen ganz ähnliche Leistungen oder Merkmale entwickeln (z.B. EEG-analoge Aktivitätsmuster). Zwar darf das nicht zu voreiligen Schlußfolgerungen verleiten, da andere Eigenschaften nicht berücksichtigt bleiben und auch verschiedene, strukturell ganz unterschiedliche Mechanismen jeweils in bestimmter Hinsicht sehr ähnliche Phänomene erzeugen können (etwa Spiralmuster). Zusätzlich sind daher detailierte Einzeluntersuchungen notwendig. Holistische und reduktionistische Ansätze ergänzen und bedingen sich also wechselseitig. Doch wenn der Rückschluß von globalen Gesetzmäßigkeiten auf lokale Strukturen auch nicht eindeutig ist, kann er immerhin zur Widerlegung von möglichen Erklärungen führen und eröffnet damit gute Chancen, bottom up-Hypothesen zu testen.

R.V.

Lit.: Basar, E. u.a. (Hrsg.): Synergetics of the Brain. Berlin u.a. 1983. Casti, J.L.: Complexification. New York 1994. Davies, P.: Prinzip Chaos. München 1988. Ebeling, W., Feistel, R.: Chaos und Kosmos. Berlin, Heidelberg, Oxford 1994. Freeman, W.J.: Physiologie und Simulation der Geruchswahrnehmung. Spektrum der Wissenschaft 4 (1991), S. 60-69. Freeman, W.J.: Tutorial on neurobiology: from single neurons to brain chaos. International Journal of Bifurcation and Chaos 2 (1992), S. 451-482. Freeman, W.J.: Societies of Brains. Hillsdale 1995. Freeman, W.J.: How Brains Make Up Their Minds. London 1999. Fuchs, A., Jirsa, V.K.: The HKB Model Revisited. Human Movement Science 19 (2001), S. 425-449. Haken, H.: Erfolgsgeheimnisse der Natur. Stuttgart 1980. Haken, H.: Synergetik. Berlin u.a. 1981. Haken, H.: Advanced Synergetics. Berlin u.a. 1983. Haken, H. (Hrsg.): Computational Systems – Natural and Artificial. Berlin u.a. 1987. Haken, H.: Information and Self-Organisation. Berlin u.a. 2000. Haken, H.: Synergetic Computers and Cognition. Berlin u.a. 1991. Haken, H.: Principles of Brain Functioning. Berlin, Heidelberg, New York 1996. Haken, H., Haken-Krell, M.: Erfolgsgeheimnisse der Wahrnehmung. Stuttgart 1992. Haken, H., Haken-Krell, M.: Gehirn und Verhalten. Stuttgart 1997. Haken, H., Stadler, M. (Hrsg.): Synergetics of Cognition. Berlin u.a. 1990. Haken, H., Wunderlin, A.: Die Selbststrukturierung der Materie. Braunschweig 1991. Hansch, D.: Psychosynergetik. Opladen 1997. Jirsa, V.K., Vaas, R.: Selbstorganisation und Gehirn. Grenzgebiete der Wissenschaft 44 (1995), S. 157-180. Kauffman, S.A.: The Origins of Order. New York 1993. Kauffman, S.A.: At Home in the Universe. New York 1996. Kelso, J.A.S.: Dynamic Patterns. Cambridge 1997. Kratky, K.W., Wallner, F. (Hrsg.): Grundprinzipien der Selbstorganisation. Darmstadt 1990. Krohn, W., Küppers, G. (Hrsg.): Selbstorganisation. Braunschweig, Wiesbaden 1990. Mishra, R.K., Maaß, D., Zwierlein, E. (Hrsg.): On Self-Organization. Berlin, Heidelberg, New York 1994. Nicolis, G., Prigogine, I.: Die Erforschung des Komplexen. München 1987. Nuñez, P.L.: Electric Fields of the Brain. New York 1981. Nuñez, P.L.: Neocortical Dynamics and Human EEG Rhythms. New York 1995. Nuñez, P.L.: Toward a Quantitative Description of Large Scale Neocortical Dynamic Function and EEG. Behavioral and Brain Sciences 23 (2000), Nr. 3. Prigogine, I.: Vom Sein zum Werden. München 1988. Prigogine, I., Stengers, I.: Dialog mit der Natur. München 1981. Schuster, H.-G.: Deterministic Chaos. Weinheim 1988. Skarda, C.A., Freeman, W.J.: How brains make chaos in order to make sense of the world. Behavioral Brain Sciences 10 (1987), S. 161-195. Vaas, R.: Die Welt als Würfelspiel. In: Evangelische Akademie Baden (Hrsg.): "Gott würfelt (nicht)!". Karlsruhe 1993, S. 108-162.

Selbstorganisation

Im Bereich der künstlichen neuronalen Netze wird der Begriff der Selbstorganisation vor allem mit dem unüberwachten Lernen in Verbindung gebracht. Hierbei werden die synaptischen Gewichte von lokal miteinander verbundenen Neuronen auf der Basis der neuronalen Eingaben und der neuronalen Aktivität anhand lokaler Lernregeln adaptiert, und zwar ohne Einbeziehung eines externen Lehrersignals. Kohonen-Netz.

Selbstorganisation

Vereinfachter Vergleich zwischen traditionellen reduktionistischen und synergetischen Ansätzen zur Erforschung von Gehirnfunktionen

Selbstorganisation

Abb. 1: Die Entwicklung des stationären Zustands U₀ eines komplexen Systems in Abhängigkeit eines Kontrollparameters σ. Siehe Grundtext.

Selbstorganisation

Abb. 2: Schematische Darstellung der Synergetik zur Beschreibung der räumlichen oder zeitlichen Dynamik komplexer Systeme.

Selbstorganisation

Abb. 3: Phasenübergang in einem Koordinationsexperiment: Bewegt man die Zeigefinger beider Hände jeweils beide nach rechts, dann nach links und wieder nach rechts usw. und steigert die Frequenz dieser gegenphasigen Bewegungen kontinuierlich, kommt es plötzlich und unwillkürlich zum Umschlag in die Gleichphase, und beide Finger bewegen sich nun jeweils aufeinander zu oder voneinander weg. Die Synergetik hat einen formalen Rahmen entwickelt, um solche und andere Selbstorganisationsvorgänge zu erklären.

Selbstorganisation

Abb. 4: Graphische Darstellung der Dynamik des HKB-Modells zur Beschreibung eines bistabilen Zustands, der in einen monostabilen übergeht. Damit können z.B. Wechselwirkungen zwischen äußeren Reizen und Gehirnprozessen modelliert werden. Details siehe Grundtext.

Selbstorganisation

Reduktionismus und Emergenz:
Es ist wichtig zu sehen, daß die reduktionistischen und holistischen Ansätze sich keineswegs ausschließen müssen, sondern sich vielmehr ergänzen können. Gerade aufgrund der praktischen Beschränkungen des bottom up approach ist der top down approach eine fruchtbare Alternative, die die Systemeigenschaften zu beschreiben und ihr Zustandekommen zu erklären versucht, ohne daß die Gültigkeit der Gesetze auf den tieferen Ebenen verletzt wäre. Dies spricht für die Vereinbarkeit der unterschiedlichen Forschungsstrategien und ihren Ergebnissen. Von daher kann trotz praktischer, methodischer und epistemischer Schwierigkeiten, emergente, makroskopische Phänomene aus den zugrundeliegenden mikroskopischen Prozessen approximativ oder möglicherweise sogar prinzipiell abzuleiten, die Auffassung von einer Einheit und physikalischen Abgeschlossenheit der Welt und somit ein ontologischer Monismus beibehalten werden. Auch qualitativ neue Eigenschaften eines Systems lassen sich deshalb als von den komplexen Wechselwirkungen und Konfigurationen seiner Komponenten unter geeigneten Randbedingungen hervorgebracht begreifen. Daß diese Emergenz niemals in allen Details nachvollziehbar und somit reduzierbar ist, widerspricht diesem ontologischen Monismus nicht. Vielmehr erklären die Theorien des Komplexen, warum eine solche Totalanalyse nicht durchführbar sein kann. Sie eröffnen jedoch auch neue Einsichten in die Prinzipien der Selbstorganisation und -bildung solcher Systemeigenschaften und ermöglichen Informationskompression und Komplexitätsreduktion und damit die Formulierung übergreifender Gesetzmäßigkeiten, die ein Verständnis und in Einzelfällen auch Vorhersagen und gezielte Manipulationen dort noch erlauben, wo der bottom up approach versagt oder sogar versagen muß. Darüber hinaus werden erstmals einheitliche Prinzipien der Strukturbildung und Entstehung von Ordnung aus Unordnung in ganz unterschiedlichen Systemen erkennbar, die die Wirkung darwinistischer Prinzipien auch in der unbelebten Welt aufzeigen und das universelle Ineinandergreifen von Zufall und Notwendigkeit ahnen lassen.