Lexikon der Optik: Aberrationen
Aberrationen, 1) allgemein, unkorrekt als Abbildungsfehler, Bildfehler oder Linsenfehler bezeichnete Abweichungen vom Strahlverlauf der Gaußschen Abbildung, vor allem von der Strahlenvereinigung im Bildpunkt, die aus der Diskrepanz zwischen den mathematischen Transformationen der Gaußschen Abbildung und dem Brechungsgesetz, vor allem bei der Abbildung ausgedehnter Objekte, notwendig folgen und sich deshalb nie exakt beseitigen, sondern nur teilweise kompensieren lassen, wobei Zonenfehler bleiben. Durch Verschiebung und Verbreiterung der Bildpunkte zu z.T. nicht rotationssymmetrischen Zerstreuungsfiguren erzeugen A. Maßstabsverzerrungen und Verluste an Kontrast, Auflösung und damit an Bildgüte. Bei Defokussierung der Auffangebene verändern sich die Zerstreuungsfiguren. Die kleinste Zerstreuung liegt im allgemeinen nicht in der Gaußschen Bildebene, sondern bildhöhenabhängig in einer gekrümmten Bildschale vor.
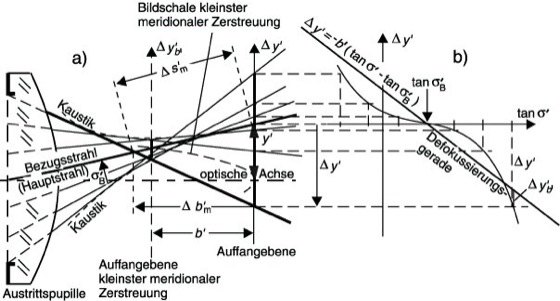
Man unterscheidet die dispersionsbedingten, auch im paraxialen Gebiet auftretenden chromatischen Aberrationen und die mit dem Einfallswinkel und damit der Strahlablenkung an den optischen Flächen wachsenden monochromatischen A., die für kleine Einfallswinkel ε ≈ sinε ≈ tanε, d.h. im paraxialen Gebiet verschwinden oder durch geeignete Durchbiegung und Aufspaltung der Linsen in viele Flächen mit kleiner Strahlablenkung verringert werden können (Korrektion). Die monochromatischen A. verursachen die Kaustik. Sie werden in der Auffangebene als Durchstoßpunkte der vom Objektpunkt ausgehenden Strahlen erfaßt (Spotdiagramm). Die mittlere quadratische Abweichung dieser Punkte von einem Bezugspunkt (Bildpunkt) ist das Gaußsche Moment. Die meridionale und die sagittale Komponente der Strahlabweichung sind die Queraberrationen Δy' und Δx' (Abb. 1). Meridionalstrahlen haben nur meridionale A., die in Abhängigkeit von der Strahlneigung tanσ' gegenüber der optischen Achse graphisch dargestellt werden. Die Ablagen Δy'b' dieser Queraberrationskurven Δy'(tanσ') von der Geraden Δy'= -b'(tanσ'-tanσ ![]()
) geben die Queraberrationen in einer um b' defokussierten Auffangebene an (tanσ ![]()
Bezugsstrahlneigung, Abb. 2).
Veraltet ist die Verwendung der nur auf Meridionalstrahlen anwendbaren Längsaberrationen, die entweder als Schnittweitenaberrationen, d.h. als Abstand des Schnittpunktes zwischen Meridional- und Bezugsstrahl vom Bezugspunkt in der Auffangebene oder als Defokussierung Δb' dieses Schnittpunktes gegenüber der Auffangebene definiert sind (Abb. 2).
Die A. sind komplizierte Funktionen der Objekthöhe y und der Pupillenkoordinaten h ![]()
, ϕ ![]()
; sie lassen sich nur näherungsweise über die Potenzreihenentwicklung der Winkelfunktionen der Strahlwinkel ![]()
analytisch darstellen: 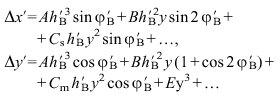
Entsprechend ihrer Abhängigkeit von y lassen sich die A. in die y-unabhängige sphärische Aberration, in die zu y bzw. y2 proportionale Koma bzw. die meridionale und die sagittale Bildfeldwölbung, deren Differenz den Astigmatismus definiert, und in die nur von y und nicht von h ![]()
abhängige Verzeichnung einteilen. Bis auf die sphärische A. treten diese A. nie einzeln, sondern überlagert auf. Die A. 3. Ordnung erfaßt die Seidelsche Bildfehlertheorie, deren Bildfehlerkoeffizienten A, B, Cm bzw. Cs und E für die sphärische Aberration, für die Koma, für die meridionale bzw. für die sagittale Bildfeldwölbung und für die Verzeichnung die Seidelschen Summen von Flächen- oder Linsenteilkoeffizienten sind, die ihrerseits analytisch als Funktionen der Radien, Brechzahlen und Abstände der Linsenflächen darstellbar sind. Selbst die nicht mehr so übersichtliche Bildfehlertheorie 5. Ordnung reicht für die Berechnung der A. moderner optischer Systeme nicht aus und wird deshalb nur für den Systemansatz und zur Vorkorrektion benutzt.
Da die Lichtstrahlen Wellennormalen sind, führen A. zu Deformationen der Wellenflächen (Wellenaberration), die als Phasenstörungen partielle Interferenzen erzeugen, die die Punktbildverwaschung durch bildgüteverschlechternde Intensitätsumverteilung negativ beeinflussen.
2) Aberration des Auges, Abbildungsfehler des Auges. Wie andere brechende optische Systeme weist auch das Auge Abbildungsfehler auf, die das Auflösungsvermögen und die Qualität des Netzhautbildes begrenzen.
a) Sphärische Aberration (Öffnungsfehler). Es werden innere und äußere sphärische A. unterschieden. Die äußere sphärische A. bezieht sich auf das Licht, das von der Netzhaut ausgehend das Auge verläßt. Die innere sphärische A. (ISA) betrifft das Licht, das in das Auge hineingelangt. Sie ist gegeben durch die Brennweitendifferenz zwischen einem im Abstand y von der optischen Achse auf das Auge auftreffenden und einem paraxialen Strahl. Bezogen auf den bildseitigen Hauptpunkt des Auges ist die ISA (in dpt) gegeben durch
ISA=n/l'y-n/l'0,
wobei n die Brechzahl des Glaskörpers ist. Die Strecken l'y und l'0 sind die Abstände der Brennpunkte eines in der Höhe y einfallenden Strahles und eines Paraxialstrahles vom bildseitigen Hauptpunkt des Auges.
Die sphärische A. des Gullstrand-Auges ändert sich mit dem Quadrat der Einfallshöhe des einfallenden Strahles. Sie läßt sich beim akkommodationslosen Gullstrand-Auge durch die Beziehung
ISA=0,44 y2 [dpt]
annähern, wobei y die Einfallshöhe in mm ist. Die sphärische Aberration des Gullstrand-Auges bei maximaler Akkommodation ist durch
ISA=0,65 y2 [dpt]
gegeben.
Das Auge verfügt über einige Kompensationsmechanismen, die die sphärische A. begrenzen. Die Hornhaut weist keine sphärische Geometrie auf, sie ist in ihrer Peripherie abgeflacht. Die Augenlinse besitzt eine gradientenförmige Verteilung der Brechzahl. Lichtstrahlen, die durch das Zentrum der Pupille hindurchtreten, führen zu einer stärkeren Empfindung als achsferne Strahlen, die peripher die Pupille passieren (Stiles-Crawford-Effekt). Die Zunahme der sphärischen A. bei der Nahakkommodation wird durch die gleichzeitig auftretende Verengung der Pupille begrenzt.
b) Chromatische Aberration. Sie ist durch die Brechzahlabhängigkeit der verschiedenen Augenmedien bedingt. Der chromatische Brechwertunterschied des Gullstrand-Auges zwischen den Wellenlängen 380 nm und 780 nm beträgt rund 3,5 dpt. Für das Wellenlängenintervall zwischen der F'- und der C'-Linie macht der Brechwertunterschied rund 1,2 dpt aus. Der Brechwertunterschied des Auges ist experimentell sehr schwer zu bestimmen. Klinisch bedeutsamer ist die Refraktionsdifferenz des Auges. Im Blauen entspricht die chromatische Refraktionsdifferenz Myopien von -1 bis -2 dpt, während im Roten Hyperopien von rund 0,5 dpt vorliegen. Als Einstellwellenlänge, bei der das Auge emmetrop ist, wird ein Wert von 586,7 nm (Helium-d-Linie) angenommen. Das Auge verfügt über zwei Kompensationsmechanismen, mit denen es den Einfluß der chromatischen A. auf die Wahrnehmung begrenzen kann. In der Foveola, der Stelle des schärfsten Sehens, befinden sich keine S-Zapfen. Blaues Licht, das in großen Zerstreuungskreisen auf die Netzhaut abgebildet wird, wird in der Foveola nicht absorbiert und kann somit keinen störenden Einfluß auf die Wahrnehmung haben. Weiterhin ist in der Makula vor den Außensegmenten der Rezeptoren ein gelbes Photopigment (Xanthophyll), das blaues Licht absorbiert, eingelagert. Der Anteil blauen Lichtes, der zu den Außensegmenten der Rezeptoren gelangt, ist hierdurch vermindert.
c) Dezentrische Aberrationen. Das Auge ist kein zentriertes System. Infolge der ungenügenden Zentrierung der abbildenden Strukturen des Auges zeigt das bilderzeugende Strahlenbüschel Asymmetrien, die einen Astigmatismus zur Folge haben.
d) Diffraktive Aberration. Sie ist die Folge der Lichtbeugung am Pupillenrand. Punktförmige Objektpunkte werden als Beugungsscheibchen auf die Netzhaut abgebildet. Aus der Theorie der Beugung an einer kreisförmigen Öffnung ergibt sich bei einem Durchmesser der Eintrittspupille des Auges von 2,4 mm, einer Brennweite von 22,2 mm und einer Lichtwellenlänge von 550 nm ein Durchmesser des Beugungsscheibchens von 6,2 μm, was näherungsweise dem dreifachen Durchmesser eines Rezeptors entspricht.

Aberrationen 1: Windschiefer Strahl mit meridionaler (Δy') und sagittaler (Δx') Queraberrationskomponente.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.