absorbierende Kristalle. Die Schwächung des Lichtes in derartigen Kristallen hängt im allgemeinen von der Durchstrahlungsrichtung ab. Um diesen Sachverhalt zu beschreiben, ist der symmetrische Dielektrizitätstensor ε₀ε_ik (Kristalloptik) durch einen tensoriellen, frequenzabhängigen Absorptionsanteil zu ergänzen. Man führt so den komplexen Dielektrizitätstensor


(1)

(i,k=1, 2, 3 bzw. x,y,z)

ein, wobei ε₀ die Dielektrizitätskonstante des Vakuums, ω die Kreisfrequenz des Lichtes und σ_ik einen symmetrischen Leitfähigkeitstensor bezeichnen (Metalloptik). Wir vernachlässigen die räumliche Dispersion, d.h. die optische Aktivität. Der Tensor σ_ik kann als Fläche 2. Ordnung Σ_i,kσ_ikx_ix_k=1 (Leitfähigkeitsfläche) dargestellt werden. Ihre Achsen, die Absorptionsachsen, fallen mit den optischen Symmetrieachsen (Kristalloptik) zusammen, ausgenommen das monokline und das trikline Kristallsystem. Der komplexe Tensor

_ik der relativen Dielektrizitätskonstanten führt über eine im allgemeinen komplexe Hauptachsentransformation zu drei komplexen Hauptdielektrizitätskonstanten

_i, die mit den komplexen Hauptbrechungsindizes

_i in Analogie zum absorptionsfreien Fall über die Beziehung

_i=

² verknüpft sind. Werden die drei komplexen Hauptbrechungsindizes

_i anstelle der reellen Hauptbrechungsindizes in die mit dem Quadrat der Lichtgeschwindigkeit c multiplizierte Fresnelsche Normalengleichung (Kristalloptik, Gl. (5) mit der Ersetzung

usw.) eingesetzt, so entsteht die Bestimmungsgleichung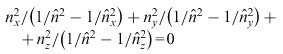

für zwei komplexe Brechungsindizes

₁ und

₂, deren Realteile die reellen Brechungsindizes und deren Imaginärteile Κ die spektralen Absorptionszahlen für die beiden sich längs der Normalenrichtung n=(n_x, n_y, n_z) ausbreitenden ebenen Wellen bedeuten. Wenn die beiden Brechungsindizes längs der Richtung n aufgetragen werden, erhalten wir die Indexfläche (Kristalloptik). Wenn analog die beiden Absorptionszahlen aufgetragen werden, ergibt sich die zweischalige Absorptionsfläche. In Analogie zur Kristalloptik kann das einschalige Absorptionsovaloid mit entsprechenden Absorptionsbinormalen (Normalenrichtungen, bei denen die Absorption für beide Polarisationsfälle gleich ist) definiert werden.

Für den Sonderfall schwach absorbierender und schwach doppelbrechender Kristalle kann nach E. Mallard eine einschalige Absorptionsfläche in Form eines dreiachsigen Ellipsoids angegeben werden (Mallardsche Absorptionsfläche). Ähnlich wie bei der Fletcherschen Indikatrix (Kristalloptik) besitzt die Schnittellipse dieser Fläche mit einer Ebene senkrecht zur Wellennormalenrichtung zwei Halbachsen, die parallel zu den Lichtschwingungsrichtungen sind. Die Längen dieser Halbachsen stellen die Kehrwerte der Wurzeln aus den zugehörigen Absorptionszahlen dar. Bei optisch einachsigen absorbierenden, nicht aktiven Kristallen gehören zu jeder beliebigen Wellennormalenrichtung zwei linear und senkrecht zueinander polarisierte Wellen, deren Schwingungsrichtungen parallel bzw. senkrecht zu dem die betreffende Wellennormale enthaltenden Hauptschnitt sind.

Bei optisch zweiachsigen absorbierenden, nicht aktiven Kristallen treten im allgemeinen zwei elliptisch polarisierte Ausbreitungsmoden auf, deren einander ähnliche Schwingungsellipsen gleichsinnig durchlaufen werden. Die großen Halbachsen der Schwingungsellipsen sind zueinander gekreuzt. Speziell gibt es auf Kegeln angeordnete Wellennormalenrichtungen, zu denen zwei linear und senkrecht zueinander polarisierte Wellentypen gehören. Weiterhin gibt es in zweiachsigen Kristallen vier Wellennormalenrichtungen, die Windungsachsen oder singulären Achsen, entlang deren sich zirkular polarisierte Wellen ausbreiten. In diesen vier Fällen sind die Brechungsindizes und die Absorptionszahlen für beide Ausbreitungsmoden einander gleich. Mit schwächer werdender Absorption nähern sich je zwei Windungsachsen, zu denen zwei entgegengesetzt zirkular polarisierte Wellen gehören, einer Binormalen.

Wenn der durch die Beziehung

mit n als reellem Brechungsindex definierte Absorptionsindex Κ' klein gegen 1 ist, spricht man von schwach a. K. Dann entsprechen die Polarisationsverhältnisse fast denen bei Kristallen ohne Absorption, da sich die elliptische Polarisation stark der linearen annähert. Ausgenommen hiervon ist die Umgebung der Windungsachsen bzw. der Binormalen. Wenn die Absorptionsachsen mit den optischen Symmetrieachsen zusammenfallen, können bezüglich der letzteren in Analogie zu den Brechungsindizes Hauptabsorptionsindizes definiert werden. Bei einachsigen Kristallen ergeben sich der ordentliche und der außerordentliche Absorptionsindex.

Die Behandlung anisotroper negativer Absorption ("gain" in verstärkenden Medien) war bisher noch nicht notwendig, könnte aber analog zu der vorhandenen Theorie der Absorption durchgeführt werden.

Eine anisotrope Absorption kann außer in Kristallen auch noch durch Orientierung von anisotrop absorbierenden Molekülen in einer Richtung (z.B. Farbstoffe) hervorgerufen werden, beispielsweise durch ein äußeres Feld oder durch mechanische Deformation (Polarisationsfolie, Polarisationsfilter).

Die Wirkung des Turmalins als Polarisator beruht auf anisotroper Absorption, wobei das Licht der einen Polarisationsrichtung viel stärker absorbiert wird als das der anderen (ordentlicher Absorptionsindex Κ'_o=1,34·10^-4, außerordentlicher Absorptionsindex Κ'_e=1,56·10^-5 bei der Wellenlänge λ=589 nm). Die zugehörige zweischalige Absorptionsfläche ist in der Abb. skizziert.

Die Wellenlängenabhängigkeit der anisotropen Absorption führt zu Pleochroismus.

Absorbierende Kristalle: Zweischalige Absorptionsfläche für Turmalin. Κ'_o, Κ'_e Absorptionsindex für die ordentliche bzw. außerordentliche Welle.