aplanatische Spiegelsysteme, vornehmlich für astrophotographische Zwecke entwickelte Spiegelteleskopsysteme. Bei ihnen wird durch Erfüllung der Sinusbedingung erreicht, daß ein größeres Bildfeld komafrei wird. Bei den klassischen Spiegelteleskopen mit einem Parabolspiegel als Hauptspiegel ist insbesondere bei großem Öffnungsverhältnis nur ein sehr kleines Bildfeld in der Nähe der optischen Achse für die Beobachtung brauchbar. Die außerhalb der Achse auftretenden Zerstreuungsfiguren wachsen linear mit zunehmendem Abstande von der Achse und proportional mit dem Quadrate des Öffnungsverhältnisses. Da bei visuellen Beobachtungen bei stärkeren Vergrößerungen ohnehin nur ein sehr kleines Gesichtsfeld benutzt wird, stört die Koma hier wenig. Für die photographische Aufnahme größerer Bildfelder sind die klassischen Spiegelteleskope jedoch unbrauchbar. Seit der Jahrhundertwende war man deshalb bestrebt, Spiegelsysteme zu entwickeln, die diese Mängel nicht aufweisen. Es sind so eine Anzahl Spiegelsysteme entstanden, die nach Art des optischen Aufbaus in folgende Hauptgruppen gegliedert werden können:

1) Korrektionssysteme zu parabolischen Hauptspiegeln. Diese Systeme sind dort von Bedeutung, wo der Hauptspiegel eines großen Spiegelteleskops wahlweise entweder mit Zusatzsystem für Aufnahmen großer Himmelsfelder oder ohne Zusatzsystem bei Beschränkung auf kleine Bildfelder für das Arbeiten direkt im Newton-, Cassegrain- oder Coudé-Fokus benutzt werden soll. Die Korrektion der außeraxialen Fehler des Parabolspiegels kann entweder durch Linsensysteme oder durch Spiegelsysteme erfolgen. Von F. E. Ross wurden Linsenkorrektionssysteme (Ross-Linsensysteme) berechnet (Abb. 1 a). Sie wurden mit Erfolg bei den großen Spiegelteleskopen des Mount-Wilson- und des Mount-Palomar-Observatoriums angewandt. Das nutzbare Bildfeld wird bei diesem System etwa um den Faktor 10 vergrößert. Ein dreiteiliges dioptrisches Korrektionssystem für Parabolspiegel wurde von J. G. Baker entwickelt. Es besteht aus einer Korrektionsplatte nach Art der unter 3) angeführten Schmidt-Platte von gleicher Größe wie der Parabolspiegel, die im Abstande von etwa 1/5 bis 1/6 der Brennweite vor dem Brennpunkte des Parabolspiegels angeordnet ist, und einem kleinen zweiteiligen achromatischen System im konvergenten Strahlengang (Abb. 1 b). Ein Spiegelkorrektionssystem wurde von J. Picht 1951 beschrieben. Es besteht aus zwei Spiegeln, die vor dem Brennpunkte in den konvergenten Strahlengang des Parabolspiegels eingefügt sind (Abb. 1 c).

2) Aplanatische Zweispiegelsysteme. Von K. Schwarzschild wurde 1905 eine Reihe von Spiegelsystemen angegeben, die bei einem Öffnungsverhältnis von 1:3,5 für ein größeres Bildfeld von fast 3° Ausdehnung brauchbar sind. Abb. 1 d zeigt einen optimalen Typ. Beide Spiegel sind Hohlspiegel und asphärisch deformiert. Ein reelles Zwischenbild kommt nicht zustande. Die Abschattung durch den Sekundärspiegel ist reichlich groß. Das Spiegelsystem ist wegen der großen Deformation aus technischen Gründen schwer zu realisieren. Das Chretién-System (Abb. 1 e) ist aus dem Cassegrainschen Spiegelteleskop hervorgegangen und diesem äußerlich ganz ähnlich. Die Meridiankurven der beiden Spiegel weichen jedoch von einer Parabel bzw. Hyperbel ab. Das System ist bei einem Öffnungsverhältnis von 1:6,5 für ein Bildfeld von etwa 2° Ausdehnung brauchbar. Die Bildfläche ist stark gekrümmt. Neuerdings werden Chretién-Systeme nur noch in der von G. Ritchey entwickelten Variante (Ritchey-Chretién-System) benutzt. Außer den von K. Schwarzschild und H. Chretién angegebenen Systemen gibt es noch weitere Möglichkeiten für aplanatische Zweispiegelsysteme. Diese wurden in ihrer Allgemeinheit von Theissing und Zinke 1948 untersucht.

3) Schmidt-Spiegel. Das 1930 von B. Schmidt (1878-1935) entwickelte Spiegelsystem stellt die genialste Lösung für ein komafreies Spiegelsystem dar, das zudem von einfachster und übersichtlichster Form ist (Abb. 2 a). Es besteht aus einem Kugelspiegel, in dessen Krümmungsmittelpunkte (im Abstand der doppelten Brennweite 2f) eine Öffnungsblende angeordnet ist. Die Bildfläche befindet sich in der Mitte zwischen dem Kugelspiegel und der Öffnungsblende und ist gekrümmt (die konvexe Seite dem Spiegel zugewandt, Radius der Bildfläche gleich f). Da Strahlenbündel jeder Richtung, welche durch die Öffnungsblende auf den Spiegel treffen, unter gleichen Bedingungen vereinigt werden, treten hier außeraxiale Fehler wie Koma und Astigmatismus überhaupt nicht auf. Die sphärische Aberration beseitigte Schmidt durch eine am Orte der Öffnungsblende befindliche dünne Korrektionsplatte mit schwach ringwulstartiger Oberfläche, für deren Herstellung er ein besonderes Verfahren fand (Schmidtsche Korrektionsplatte). Eine Bildebnung kann beim Schmidt-Spiegel durch eine dicht vor der Platte befindliche schwache Sammellinse erreicht werden (Bildebnungslinse nach Piazzi-Smyth 1874). Zur Erzielung großer Öffnungsverhältnisse kann man den Strahlengang zwischen Korrektionsplatte, Hohlspiegel und Bildfläche ganz in Glas verlaufen lassen (Abb. 2 b). Als größter ausgeführter Schmidt-Spiegel sei das 2 m-Universalspiegelteleskop in Tautenburg erwähnt (Spiegelteleskop).

4) Schmidt-Cassegrain-Systeme. Zur Vermeidung der Nachteile des Original-Schmidt-Spiegels wie Bildwölbung, große Baulänge (2f) und ungünstige Lage der Bildfläche wurden eine Reihe von Modifikationen des Schmidt-Spiegels entwickelt. Zu diesen Abwandlungen gehören die Schmidt-Cassegrain-Systeme (Abb. 2 c). Sie bestehen wie das normale Cassegrain-Teleskop aus einem Hauptspiegel und einem konvexen Sekundärspiegel. Als zusätzliches optisches Element ist die Schmidtsche Korrektionsplatte hinzugekommen. Bei den von J. G. Baker untersuchten Schmidt-Cassegrain-Systemen haben beide Spiegel etwa gleich große Scheitelradien. Als freie Parameter verbleiben der Abstand der Korrektionsplatte vom Hauptspiegel (Baulänge) und der Abstand der Bildfläche vom Sekundärspiegel. Im allgemeinen sind beide Spiegel deformiert, bei Systemen mit großer Baulänge kann ein Spiegel sphärisch sein und der andere nur wenig von der sphärischen Form abweichen. Die Deformation der Korrektionsplatte ist größer als beim normalen Schmidt-Spiegel. Eine Korrektur der dadurch auftretenden chromatischen Aberration ist durch Anbringen einer achromatischen Korrektionsplatte (nach Baker) oder zweier Korrektionsplatten aus verschiedenen Gläsern mit größerem Luftabstand (nach Linfoot) möglich.

5) Meniskussysteme. Die sphärische Aberration des komafreien Kugelspiegels mit Öffnungsblende kann außer durch die Schmidtsche Korrektionsplatte auch durch einen von sphärischen Flächen begrenzten nahezu afokalen Meniskus korrigiert werden. Diese Systeme werden als Meniskussysteme bezeichnet, oder auch nach dem ersten Autor als Maksutow-Systeme. Die Erfindung erfolgte fast gleichzeitig und unabhängig voneinander durch K. Pennig, A. Bouwers, D. Gabor und D. D. Maksutow. Der Meniskus befindet sich bei diesen Systemen in der Regel zwischen dem Krümmungsmittelpunkte des Kugelspiegels und der Bildfläche. Er ist mit seiner konvexen Seite dem Spiegel zugewandt (Abb. 2d). Bei dem Sonderfalle des konzentrischen Meniskussystems fallen die beiden Krümmungsmittelpunkte des Meniskus mit dem Krümmungsmittelpunkte des Kugelspiegels zusammen (Abb. 2e). Mit den konzentrischen Meniskussystemen läßt sich zwar ein sehr großes Bildfeld erhalten, sie stellen jedoch im Hinblick auf die chromatischen und sphärischen Restfehler nicht die optimale Lösung unter den Meniskussystemen dar. Die Meniskussysteme wurden ebenfalls, wie der Original-Schmidt-Spiegel, auf verschiedene Weise abgewandelt, z.B. auch als Meniskus-Cassegrain-Systeme. Man kommt so zu sehr kurzen Baulängen und kann bei geringem Aufwande an optischen Elementen nur mit sphärischen Flächen lichtstarke und leistungsfähige Instrumente schaffen, die z.B. für Fernobjektive (Abb. 3a) oder als Visierfernrohre für geodätische Instrumente (Abb. 3b) ein zunehmendes Interesse gefunden haben. Wenn es erforderlich ist, kann chromatische Aberration des Meniskus (unter Einschränkung der Symmetrieeigenschaften) durch einen achromatischen Meniskus korrigiert werden. Die Anwendung der Meniskussysteme für große astronomische Instrumente ist begrenzt, weil es nicht möglich und auch nicht sinnvoll ist, einen Meniskus in sehr großen Dimensionen herzustellen. Hier ist der Schmidt-Spiegel überlegen.

6) Aplanatische Spiegelsysteme mit Linsenkorrektionsglied. Diese Systeme sind dem Schmidt-Spiegel und den Meniskussystemen verwandt. Dies wird besonders deutlich bei einem Spiegelsystem von Richter und Slevogt (1941), welches sich nur dadurch vom Schmidt-Spiegel unterscheidet, daß es an Stelle der Korrektionsplatte ein zweilinsiges achromatisches afokales Korrektionssystem besitzt (Abb. 3c). Ein ähnliches System mit verkürzter Baulänge haben Richter und Slevogt ebenfalls 1941 beschrieben. Die vierte Fläche des afokalen Linsenkorrktursystems ist plan und im zentralen Teile verspiegelt, so daß, wie bei dem Cassegrain-System, die Bildfläche zum Objekt zu liegt (Abb. 3d).

Eine weitere Gruppe von aplanatischen Spiegelsystemen mit Linsenkorrektionsglied ist dadurch gekennzeichnet, daß die Korrektionsglieder ganz oder teilweise im konvergenten Strahlengange liegen. Hierher gehört unter anderem ein Spiegelsystem von A. Sonnefeld (1935), welches einen deformierten Hauptspiegel und ein nahezu afokales zweiteiliges achromatisches Korrektionssystem im konvergenten Strahlengange nahe der Bildfläche besitzt (Abb. 3e). Maksutow hat auch ein Meniskussystem beschrieben, bei dem ein Meniskus in kleiner Ausführung im konvergenten Strahlengange zur Korrektion dient.

Eine Mittelstellung zwischen den Systemen mit Linsenkorrekturglied im parallelen und denen im konvergenten Strahlengange nimmt ein Spiegelsystem von H. Slevogt ein, welches eine schwache, von sphärischen Flächen begrenzte Korrektionslinse besitzt, die, zwischen Spiegel und Bildfläche angeordnet, die gleiche Größe wie der Spiegel hat und so zweimal vom Licht durchsetzt wird (Abb. 4a).

7) Super-Schmidt-Systeme. Für extrem hohe Lichtstärken und extrem große Bildwinkel wurden Systeme entwickelt, die Kombinationen von Schmidt-Spiegel und Meniskussystemen darstellen. Systeme mit einfachem Meniskus und Schmidt-Platte (Abb. 4b) wurden von A. Bouwers 1945 und von Hawkins und E. H. Linfoot 1945 beschrieben. Die Baulänge ist etwa von gleicher Größe wie beim Schmidt-Spiegel, das nutzbare Bildfeld ist bei großem Öffnungsverhältnis erheblich größer. Die Schmidt-Platte ist nur sehr schwach deformiert. C. G. Wynne hat 1947 ein Super-Schmidt-System mit zwei nahezu konzentrisch zu einer Öffnungsblende angeordneten Menisken angegeben (Abb. 4c). J. G. Baker hat zu zwei nahezu konzentrischen Menisken noch eine Korrektionsplatte am Orte der Öffnungsblende hinzugefügt (Abb. 4d). Das System ist bei einem Öffnungsverhältnis von 1:0,67 für ein Bildfeld von 52° brauchbar. Über die Anwendung derartiger Systeme für Meteoraufnahmen hat F. L. Whipple berichtet.

Super-Schmidt-Systeme sind für extrem lichtstarke Spektrographenkameras, für Satellitenbeobachtung (Abb. 4e) u.dgl.m. von großer Bedeutung.

8) Komplexe Systeme mit Linsenspiegel. An Stelle eines Oberflächenspiegels wurde bei einigen Spiegelsystemen auch ein rückseitig verspiegelter Linsenspiegel (Mangin-Spiegel) in Verbindung mit Linsenkorrektionssystemen benutzt, um Spiegelsysteme mit extrem großem Öffnungsverhältnis zu schaffen. Das älteste System dieser Gruppe wurde um 1930 von A. Sonnefeld entwickelt und stellt ein Spiegeltriplet dar, bestehend aus zwei Einzellinsen und einer Spiegellinse (Abb. 4f). Alle Flächen sind sphärisch. Es hat die extrem hohe Lichtstärke von 1:0,5. Im Aufbau ist eine Ähnlichkeit mit dem Schmidt-Spiegel zu erkennen; die beiden Einzellinsen übernehmen die Rolle der Korrektionsplatte. Die Eintrittspupille liegt am Orte der Hinterfläche der zwei Linsen und etwa im Krümmungsmittelpunkte des Spiegels. Bei kleinerem Öffnungsverhältnis kann der Mangin-Spiegel durch einen sphärischen Oberflächenspiegel ersetzt werden. Dann kommt man zu den unter 6) angeführten Systemen von Richter und Slevogt, die aus dem Sonnefeldschen System hervorgegangen sind. Flügge hat 1941 einige weitere Spiegelsysteme mit Mangin-Spiegel beschrieben, von denen zwei ein Linsenkorrektionssystem im konvergenten Strahlengange besitzen (Abbn. 5a und b); das Öffnungsverhältnis des einen Systems beträgt 1:0,6. Bei einem anderen System mit dem Öffnungsverhältnis 1:0,9 steht eine Linse im parallelen, eine andere im konvergenten Strahlengang. Durch eine Umlenkung über einen zentralen Planspiegel hat Flügge hier eine sehr kurze Baulänge erreicht (Abb. 5c). Die letztgenannten Systeme sind unter Verwendung allein von Kugelflächen aufgebaut.

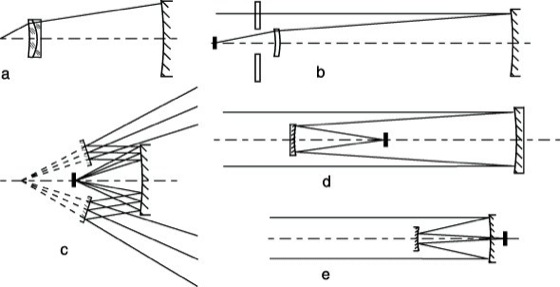
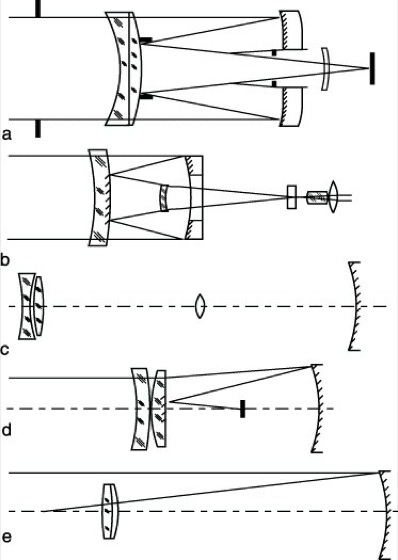
Aplanatische Spiegelsysteme 1: a) Linsenkorrektionssystem nach Ross, b) Korrektionssystem nach Baker, c) Zweispiegelkorrektionssystem nach Picht, d) Zweispiegelsystem nach Schwarzschild, e) Zweispiegelsystem nach Chretién.

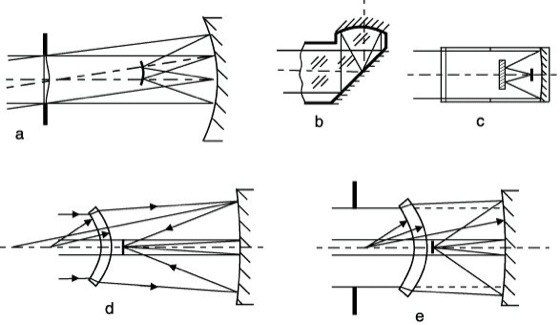
Aplanatische Spiegelsysteme 2: a) Spiegelsystem nach Schmidt, b) massiver Schmidt-Spiegel nach Hendrix, c) Schmidt-Cassegrain-System nach Baker, d) Meniskussystem nach Maksutow, e) konzentrisches Meniskussystem.

Aplanatische Spiegelsysteme 3: a) Meniskussystem als Fernobjektiv nach Bouwers, b) Meniskussystem für ein Theodolitfernrohr, c) Spiegelsystem mit Linsenkorrektion nach Richter und Slevogt, d) verkürztes Spiegelsystem mit Linsenkorrektion, e) Spiegelsystem mit Linsenkorrektion nach Sonnefeld.

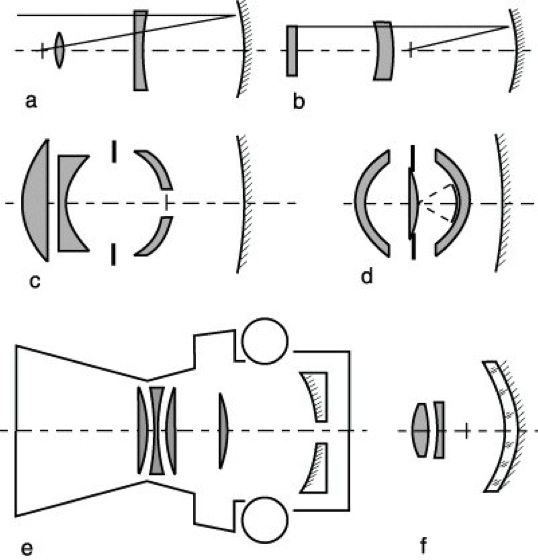
Aplanatische Spiegelsysteme 4: a) Spiegelsystem mit Linsenkorrektion nach Slevogt, b) Super-Schmidt-System nach Bouwers, c) Super-Schmidt-System nach Wynne, d) Super-Schmidt-System nach Baker, e) Baker-Nunn-Satellitenkamera, f) Spiegeltriplet nach Sonnefeld.

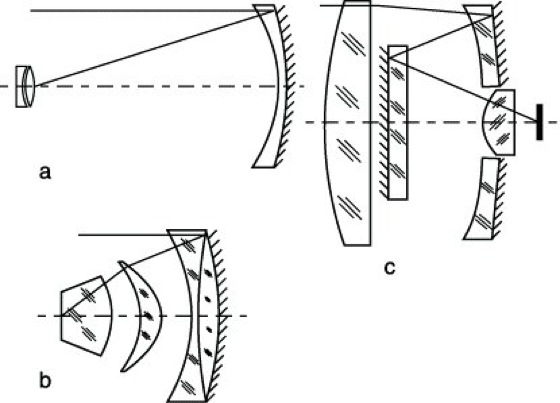
Aplanatische Spiegelsysteme 5: Spiegel-Linsen-Systeme nach Flügge.