Beugungserscheinungen, Lichterscheinungen, die in Schattengebieten auftreten, und weniger hell erscheinende Strukturen, die in beleuchteten Gebieten auftreten, infolge der Beugung. Sie sind zu beobachten, wenn Wellen bei ihrer Ausbreitung auf Hindernisse wie Blenden, Schirme, transparente oder andere Körper verschiedenster Art treffen, wobei die Gesetze der durch Strahlen beschreibbaren geometrischen Ausbreitung im allgemeinen nicht mehr gelten.

Die Beschreibung erfolgt durch die Beugungstheorie. Einige Beispiele für die Notwendigkeit der Berücksichtigung von B. in der Optik sind: B. von Licht an Blenden optischer Systeme und die damit verbundene Begrenzung des Auflösungsvermögens, Holographie, Gitter, die Abbesche Theorie des Mikroskops, die Fourier-Theorie der optischen Abbildung u.a.

Bei polychromatischem Licht können Farberscheinungen bei der Beugung wesentlich werden (z.B. bei Beugungsgittern). Spezielle B. treten bei besonderen Formen der beugenden Schirme auf. Generell sind B. an Öffnungen und dazu komplementären Schirmen durch das Babinetsche Prinzip miteinander verknüpft.

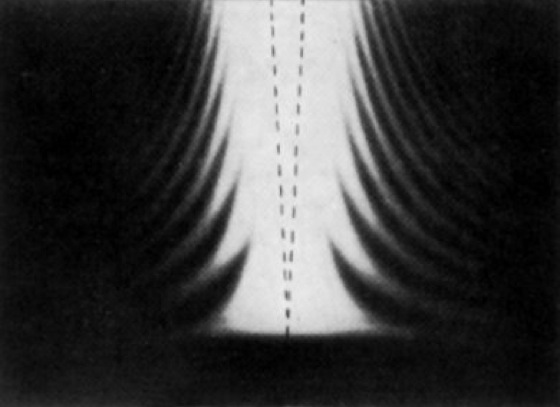
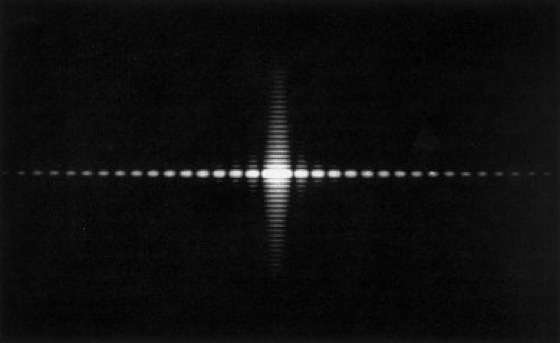
1) Beugung am Spalt. Entsprechend Abb. 1 sei ein in einer Blende B befindlicher Spalt mit senkrecht einfallendem parallelen monochromatischen Licht beleuchtet. Dann beobachtet man auf einem Schirm S, der sehr weit vom Spalt entfernt ist, ein Beugungsbild mit dem Intensitätsverlauf I, der proportional zu sinc²(bπsinβ/λ) mit sincx=(sinx)/x ist (F. M. Schwerd 1835). λ bedeutet dabei die Lichtwellenlänge. Die Minima ergeben sich aus der Bedingung sinβ_n=nλ/b, die Maxima liegen bei sinβ=0; 1,430 λ/b; 2,459 λ/b; 3,471 λ/b etc., und die Intensitäten der Maxima verhalten sich wie 1:1/20:1/56:1/100 etc. Abb. 2 zeigt das Beugungsbild eines Einzel- und eines Doppelspaltes. Das Auftreten beispielsweise des ersten Minimums kann im ersten Falle ganz elementar so erklärt werden: Man suche den Winkel β₁, für den jedem Strahl in der unteren Spalthälfte genau ein Strahl in der oberen Spalthälfte entspricht, der im Vergleich zu dem erstgenannten einen Gangunterschied von λ/2 besitzt. Dann tritt Auslöschung der beiden Strahlen zugeordneten Wellen im Fernfeld auf. Die Fraunhofersche B., die für sehr große Entfernungen zwischen B und S vorliegt, kann durch eine Linse zwischen B und S aus dem "Unendlichen" in eine Bildebene geholt werden. Sie erscheint dann in der hinteren Brennebene der Linse. Nähert sich S ohne diese Linse B, so geht die Fraunhofersche in die Fresnelsche B. über. Bei Spaltbreiten, die wesentlich kleiner als λ sind (z.B. λ/50), wird die Polarisationskomponente stärker durchgelassen, deren elektrische Feldstärke E senkrecht zum Spalt schwingt. Hingegen wird die Polarisationskomponente parallel zum Spalt wegen der Grenzbedingung E_||=0 geschwächt. Für Spaltbreiten

λ verschwinden die Unterschiede in der Transmission beider Polarisationskomponenten. Es treten aber noch Phasenunterschiede zwischen ihnen auf. Es entsteht so aus linear polarisiertem Licht elliptisch polarisiertes. Bei sehr breiten Spalten treten Streifen auch innerhalb des Gebietes auf, das nach der goemetrischen Optik völlig gleichmäßig beleuchtet sein sollte. Es handelt sich dann um die Beugung an zwei benachbarten Halbebenen.

Ein keilförmiger Spalt kann aufgefaßt werden als eine Aneinanderreihung von vielen Spalten verschiedener Breite. Die Beugungsfigur in Abb. 3 zeigt für den schmalen Teil des Spaltes ein breites zentrales Beugungsmaximum (unten) und dessen Verschmälerung sowie das Hinzutreten der Nebenmaxima im breiten Teil des Spaltes (oben). Die gestrichelten Linien geben an, wo das geometrisch-optische Bild des Spaltes liegen würde.

2) Beugung am Rechteck. Die Intensitätsverteilung für die Fraunhofersche B. an einer Rechtecköffnung der Abmessung a·b ergibt sich aus der entsprechenden Formel der Beugungstheorie durch einfache Integration zu


(1)

mit I₀ als der Intensität der einfallenden Strahlung. Hierbei ist senkrechter Einfall der Lichtwelle auf die Ebene des Rechteckes vorausgesetzt; α und β bezeichnen die Winkel, welche die Richtung des gebeugten Lichtes mit der Rechtecknormalen einschließt. In Abb. 4 ist ein Beispiel zu sehen.

Es ist in der Optik üblich, mit der ersten Nullstelle von (1), z.B. sin β₀=λ/b≈β₀, einen ersten groben Überschlag zur Abschätzung der beugungsbegrenzten Auflösung vorzunehmen. Wenn dieser Ausdruck mit der Brennweite des Instrumentes multipliziert wird, ergibt sich die Größenordnung der theoretisch zu erreichenden Auflösung.

Bei Aneinanderreihung von mehreren Rechtecken der gleichen Gestalt wird die ursprüngliche Beugungsfigur für das Einzelrechteck durch zusätzliche Nullstellen in Substrukturen, wie beispielsweise in Abb. 2b und 2c zu sehen, zerfurcht, bis sich bei periodischer Anordnung von Rechtecken ein Gitter ergibt.

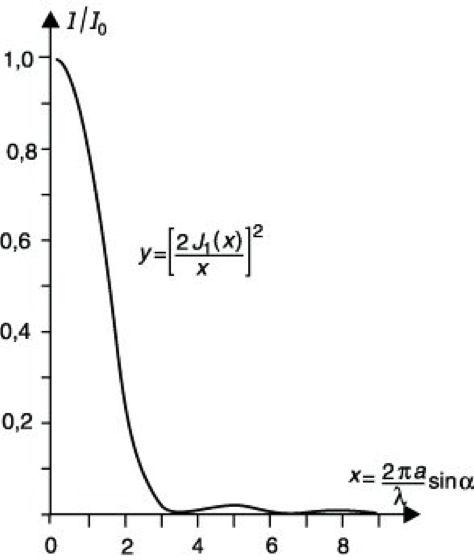
3) Beugung an einer kreisföimig begrenzten Blende. Aus der Formel für die Fraunhofersche Beugung (Beugungstheorie) ergibt sich bei senkrechtem Lichteinfall die Intensität im Fernfeld (G. B. Airy 1835) zu


(2)

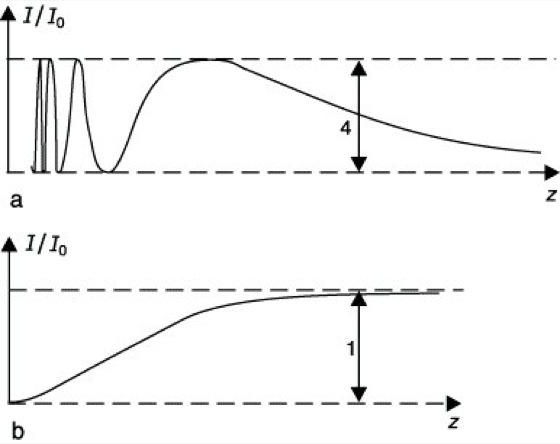
Hierbei bedeuten a den Radius der kreisförmigen Blende, α die Winkelabweichung des gebeugten Lichtes von der Normalen auf der Kreisblende und J₁ die Besselsche Funktion 1. Ordnung. Die Nullstellen von J₁(x) sind 3,8317; 7,0156; 10,1735 etc. Sie geben bei Umrechnung auf α nach der Bestimmungsgleichung 2πasinα/λ = 3,8317 usf. wegen der Rotationssymmetrie dunkle Kreise, wobei die dazwischenliegenden Maxima mit wachsendem α schnell abnehmen (Abb. 5). Die "Übersetzung" dieser Verteilung aus dem Unendlichen durch eine Linse in deren Brennebene (Ersetzung von sinα durch das Verhältnis von Brennebenen-Radialkoordinate und Brennweite f) ergibt das Airy-Scheibchen (Abb. 6). Aus dem 1. Minimum von (2) ergibt sich der Durchmesser des zentralen Lichtfleckes zu 1,219 λf/a. Bei Deformation der kreisförmigen Öffnung zu einer Ellipse wird die Airysche Beugungsfigur ebenfalls elliptisch deformiert. Dabei liegt die große Halbachse der Beugungsfigur senkrecht zur großen Halbachse der Öffnung. Weiterhin treten asteroidförmige Lichterscheinungen auf, die auf die Randwelle der Beugung (Beugungstheorie) zurückzuführen sind. Entlang der Rotationsachse kann die Fresnelsche B. für eine kreisförmige Öffnung mit dem Radius a in einem Schirm und für die dazu komplementäre undurchsichtige Kreisscheibe relativ einfach berechnet werden. Bei senkrechtem Lichteinfall ergeben sich


(3)

(Abb. 7a) für die Öffnung (z

a) und


(4)

(Abb. 7b) für die Kreisscheibe, wobei k die Wellenzahl 2π/λ, z den Abstand des Aufpunktes vom Schirm und I₀ die Lichtintensität auf dem Schirmrande bezeichnen. Hinter einer Öffnung kann es im Zentrum zu Dunkelheit kommen, hinter einer Kreisscheibe ist die Mitte immer aufgehellt. Die Wellenoptik ergibt hier eine deutliche Abweichung von den Voraussagen der geometrischen Optik. Die Aufhellung entlang der Mittennormalen hinter der Kreisscheibe wurde von S. D. Poisson 1818 theoretisch vorhergesagt und durch D. F. Arago und A. J. Fresnel nachgewiesen. Sie wird als Poissonsche Beugung oder Poissonscher Fleck bezeichnet. Bei endlicher Entfernung der Lichtquelle von der Scheibe tritt diese Aufhellung ebenfalls ein.

Wird die Beugungserscheinung für eine kreisringförmige Öffnung in Fraunhofer-Näherung der Beugungstheorie berechnet, so ergibt sich gegenüber (2) bei gleichem Durchmesser eine geringe Verschmälerung des Beugungsscheibchens bei fallendem Kontrast.

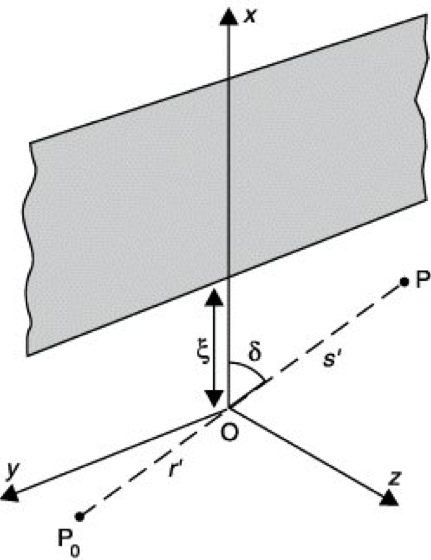
4) Beugung an der Halbebene. Die Beugung an einer schwarzen Halbebene, die das Licht vollständig absorbiert, kann mit der Fresnelschen Näherung der Kirchhoffschen Beugungstheorie behandelt werden. Entsprechend Abb. 8 sei die beugende Halbebene in der x-y-Ebene gelegen. Ihr Abstand vom Koordinatenursprung O sei ξ. Durch O gehe auch die gerade Verbindungslinie zwischen Lichtquellpunkt P₀ und Aufpunkt P, die beide in der x-y-Ebene liegen. Dann ist die Intensität in P gegeben durch


(5)


. C und S bezeichnen die beiden Fresnelschen Integrale, die mit Hilfe der Cornuschen Spirale anschaulich dargestellt werden können. Entsprechend (5) ist

(U komplexe Amplitude des Feldes) proportional zur Länge der Verbindungslinie des negativen Windungspunktes (C(-∞)=-0,5, S(-∞)=-0,5) der Cornu-Spirale mit dem Punkte der Spirale, dessen Bogenlänge vom Nullpunkt an gerechnet den Wert w hat. Die B. im beleuchteten Bereiche zeigt so, da w proportional zur transversalen Koordinaten ξ ist, in der Lichtintensität ähnliche Oszillationen wie C(w) und S(w) (Abb. 9). Im Schattengebiet (ξ~w<0) nähert sich der ξ entsprechende Spiralpunkt immer mehr dem negativen Windungspunkte, so daß dort I(P) ziemlich schnell abklingt. Praktisch stimmen die in der Fresnelschen Näherung und die mit der strengen Beugungstheorie erhaltenen Resultate für die (beiderseits spiegelnde) Halbebene mit unendlicher Leitfähigkeit überein.

Die Beugung an Schirmen beliebiger Gestalt muß im allgemeinen numerisch behandelt werden. Für Öffnungen, die durch Polygone begrenzt werden, lassen sich in Fraunhofer-Näherung analytische Formeln erhalten. Bei vorhandenem Symmetriezentrum treten Beugungslinien auf.

5) B. in der Umgebung von Bild- bzw. Brennpunkten, -linien und -flächen. Durch Blenden in optischen Systemen bedingt entsteht anstelle eines Bildpunktes bei aberrationsfreier Abbildung das Airy-Scheibchen. Aberrationen führen zu einer Aufweitung der Beugungsfigur. Durch die Beugung wird auch die Phase im Bildpunkte beeinflußt, es treten Phasenanomalien in der Nachbarschaft von Bild- bzw. Brennpunkten, -linien und -flächen auf.

6) B. an statistisch verteilten Objekten. Die B. an unregelmäßig verteilten gleich großen Öffnungen oder Teilchen (M. v. Laue 1914) ergeben sich durch Summation der Amplitudenverteilungen für die M einzelnen Öffnungen oder Teilchen. Es sei U(p, q) die Amplitudenverteilung für Fraunhofersche Beugung (Beugungstheorie) an einer Einzelöffnung bzw. einem einzelnen Teilchen im Falle senkrecht zum Schirm einfallenden Lichtes mit p und q als Richtungscosinus bezüglich der zur Ausbreitungsrichtung z senkrechten x- und y-Achse. Die gesamte Lichterregung ist dann gegeben durch


(6)

wobei x_m, y_m die Koordinaten der Zentren der Öffnungen bzw. Teilchen bezeichnen. Für die Gesamtintensität ergibt sich aus (6) das M-fache der von einem Einzelobjekt herrührenden Intensität (inkohärente Summation) und zusätzlich eine Summe, die zwar bei Mittelung über die Lagen der Zentren verschwindet, aber zu zufälligen Schwankungen der Gesamtintensität von Punkt zu Punkt Anlaß gibt. Punkte hoher Intensität wechseln mit dunkleren Stellen ("Granulation"). Unregelmäßig verteilte Phasenstrukturen wirken auf Laserlicht ebenso wie unregelmäßig verteilte Öffnungen. So beobachtet man bei Rückstreuung von Laserlicht durch eine rauhe Wand ebenfalls die Granulation als Speckle.

7) Beugung an kolloidalen TeilchenMie-Streuung, Rayleigh-Streuung.

8) Beugung in KristallenRöntgenstrahlung, Braggsche Reflexionsbedingung.

9) Beugung an UltraschallwellenDebye-Sears-Effekt.

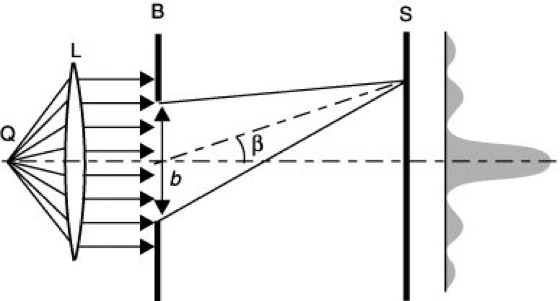
Beugungserscheinungen 1: Beugung am Spalt, Q Lichtquelle, L Linse, B Blende mit Spalt, b Spaltbreite, β Beugungswinkel, S Schirm; rechts Intensitätsverlauf im Beugungsbild.

a)

b)

c)

Beugungserscheinungen 2: Fraunhofersche Beugungsfigur eines Einzelspaltes (a) und eines Doppelspaltes (b). Den zentralen Teil von b (Youngsche Streifen) zeigt c.

Beugungserscheinungen 3: Beugung am keilförmigen Spalt.

Beugungserscheinungen 4: Fraunhofersches Beugungsbild einer rechteckigen Öffnung mit einem Seitenverhältnis a/b = 0,3.

Beugungserscheinungen 5: Fraunhofersche Beugung an einer Kreisblende vom Radius a. I/I₀ relative Intensität, α Beugungswinkel, λ Wellenlänge.

Beugungserscheinungen 6: Airysches Beugungsscheibchen.

Beugungserscheinungen 7: Fresnelsche Beugungserscheinungen auf der Achse; a) relative Intensität hinter einer kreisförmigen Öffnung und b) hinter einer Kreisscheibe.

Beugungserscheinungen 8: Zur Fresnelschen Beugung an der Halbebene.

Beugungserscheinungen 9: Beugung an einer geraden Kante. Die Kurve gibt den theoretischen Intensitätsverlauf wieder.