Beugungstheorie, die mathematische Beschreibung der unterschiedlichen Beugungserscheinungen. Die Lösung von Beugungsproblemen erfordert im Prinzip die Lösung des Systems der Maxwellschen Gleichungen unter speziellen Randbedingungen. Daher liegt allgemein ein vektorielles Beugungsproblem mit getrennter Behandlung beider Polarisationsfälle vor. Die Vereinfachung des vektoriellen Problems zur skalaren B. ist in sehr vielen praktisch bedeutsamen Fällen gerechtfertigt. Dann wird von Polarisationseffekten abgesehen und nur die Lichterregung durch eine skalare Wellenfunktion U(r, t) beschrieben, deren Absolutquadrat die Intensität angibt. Jedoch kann insbesondere bei beugenden Körpern, deren Dimension von der Größenordnung der Lichtwellenlänge ist, bei relativ schrägem Einfall auf Grenzflächen oder möglicher Anregung von Eigenschwingungen im beugenden Körper der mit der skalaren Näherung verbundene Fehler beträchtlich sein. In der Geschichte der Optik waren es vor allem drei prinzipielle Vorstellungen, mit deren Hilfe die Beugung erklärt wurde:

a) Das Huygens-Fresnelsche Prinzip (Chr. Huygens 1678, A. J. Fresnel 1816), wonach sich das Beugungsbild durch Superposition aller von einer Wellenfront ausgehenden Elementarwellen ergibt (weiterentwickelt von G. Kirchhoff 1876). b) Die Youngsche Auffassung (Th. Young 1801), daß von den Rändern eines Beugungsschirmes "reflektierte" Wellen (Beugungswellen) ausgehen, die mit der die Öffnung durchsetzenden ungestörten Welle zum resultierenden Wellenfeld interferieren (weiterentwickelt durch G. A. Maggi 1888, A. Rubinowicz 1917, V. Fock 1926). c) Die mathematische Entwicklung aller auftretenden Wellenfelder nach ebenen Wellen und Anpassung derselben an die Feldverteilung in der Ebene des Beugungsschirmes nach Lord Rayleigh (fortgesetzt von A. Sommerfeld 1894, P. Debye 1909, J. Picht 1925).

Die drei Varianten können ineinander überführt werden. Die Huygens-Fresnel-Kirchhoffsche B. konnte historisch zuerst und auf einfachem Wege quantitative Aussagen zur Beugung machen, weshalb sie meist benutzt wird.

1) Kirchhoffsche B. Prinzipiell ist bei skalaren Beugungsproblemen die Wellengleichung


(1)

bzw. die bei monochromatischer Strahlung durch Separation der hochfrequenten Zeitabhängigkeit daraus hervorgehende Helmholtz-Gleichung


(2)

zu lösen, wobei c die Lichtgeschwindigkeit und k=2π/λ die Wellenzahl (mit λ als Wellenlänge) bedeuten. Die Kirchhoffsche B. geht aus von einer mathematisch strengen Beziehung, welche die Erregung U(P) in einem beliebigem Punkte P im Inneren eines Volumens, das die Lichtquelle nicht enthält, durch die Werte der Erregung U und ihrer Ableitung ∂U/∂n längs der (nach innen zeigenden) Normalen auf der das Volumen umschließenden Fläche F ausdrückt. Die von H. v. Helmholtz 1859 abgeleitete Formel hat im Falle monochromatischer Strahlung für dreidimensionale Probleme die Gestalt


(3)

(Helmholtz-Kirchhoffsche Formel) mit s als Abstand des Flächenelementes df von P (Abb. 1). Die Funktion G=exp(iks)/s ist die Greensche Funktion der Helmholtzschen Differentialgleichung (2) im freien Raum. Sie stellt eine divergierende Kugelwelle dar. Für zweidimensionale Probleme gilt die zu (3) analoge Darstellung


(4)

(W. Weber) mit H

(ks) als erster Hankelscher Funktion vom Index Null, die eine divergierende Zylinderwelle beschreibt. Die Integration erstreckt sich längs einer geschlossenen Linie. Im Falle nichtmonochromatischer Strahlung ist anstelle von (3) die Formel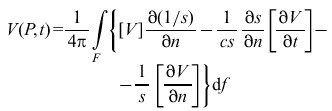


(5)

(Kirchhoff 1883) für die zeitabhängige Erregung V (ohne Separation der hochfrequenten Zeitabhängigkeit) zu verwenden, wobei c die Lichtgeschwindigkeit bezeichnet. Die eckige Klammer bedeutet, daß die Zeit in der betreffenden Funktion durch das retardierte Argument t-s/c zu ersetzen ist. Es ist bemerkenswert, daß sich eine solche allgemeine Formulierung des Huygensschen Prinzips nur für Räume mit ungeradzahliger Dimension, nicht jedoch für solche geradzahliger Dimension angeben läßt. In letzterem Falle wird nämlich die Erregung V(P, t) nicht nur durch die zur jeweiligen retardierten Zeit vorliegenden Werte von V, ∂V/∂t sowie ∂V/∂n auf einer geschlossenen Fläche (im physikalisch interessanten zweidimensionalen Falle einer geschlossenen Kurve) bestimmt, sondern außerdem durch die Werte der genannten Größen zu grundsätzlich allen früheren Zeitpunkten (V. Volterra 1912).

Bei der Anwendung von (3), (4) oder (5) auf das Problem der Beugung an einer Öffnung in einem undurchsichtigen Schirme wird die Fläche F so gewählt, daß sie durch die Öffnung geht und den Schirm enthält. Sie wird durch den Teil einer Kugelfläche (mit P als Kugelmittelpunkt) geschlossen, der in dem der Lichtquelle abgewandten Raumbereiche liegt. Letzteres Flächenstück liefert bei großer Ausdehnung des Schirmes wegen seiner großen Entfernung von P keinen Beitrag zur Erregung in P. Für eine exakte Auswertung der o.g. Beugungsformeln benötigt man jedoch die genaue Kenntnis von U und ∂U/∂n in der beugenden Öffnung und auf dem Schirme. Da diese fehlt, ist man auf Näherungsannahmen angewiesen. Kirchhoff machte die naheliegende (wenn auch mathematisch widersprüchliche) Annahme, daß die genannten Größen auf dem Schirme verschwinden und in der Öffnung genau so groß sind wie bei fehlendem Schirme. Somit ist die Integration in den Beugungsformeln nur über die beugende Öffnung zu erstrecken. Die Kirchhoffsche Annahme ist um so besser gerechtfertigt, je kleiner die Wellenlänge im Vergleich zu den Dimensionen der Öffnung ist. Sobald die Wellenlänge die Größenordnung der Ausdehnung der Öffnung erreicht, wird sie jedoch problematisch. Dieser Fall tritt jedoch in der Optik zumeist nicht auf. Tatsächlich befindet sich die Kirchhoffsche Theorie in sehr vielen Fällen in ausgezeichneter Übereinstimmung mit dem Experiment. Unter Voraussetzung einer punktförmigen Lichtquelle kann aus (3) mit den Kirchhoffschen Annahmen die Fresnel-Kirchhoffsche Beugungsformel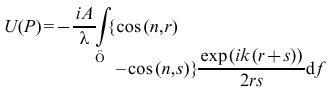


(6)

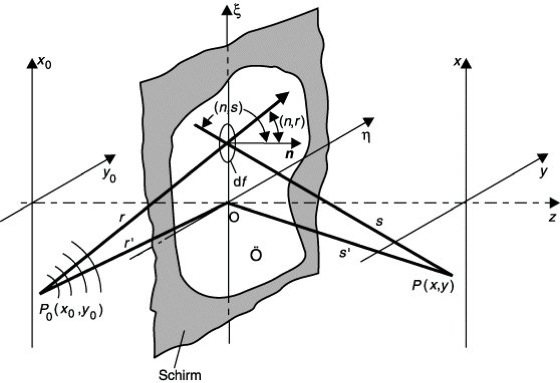
abgeleitet werden. Die Integration erstreckt sich über die beugende Öffnung und A bezeichnet die Amplitude der von P₀ ausgehenden Kugelwelle. Abb. 2 erläutert die anderen Größen. Aus (6) ist das Reziprozitäts-Theorem von Helmholtz zu entnehmen: die Punktquelle am Orte P₀ ruft an der Stelle P dieselbe Wirkung hervor, wie sie eine Punktquelle am Orte P an der Stelle P₀ erzeugt. Unter der üblicherweise erfüllten Voraussetzung, daß die Abstände des Quellpunktes P₀ und des Aufpunktes P vom Schirm groß im Vergleich zur Ausdehnung der Öffnung sind, läßt sich (6) für den Fall eines ebenen Schirmes dadurch vereinfachen, daß man die Abstände r und s im Exponenten der e-Funktion in eine Potenzreihe bezüglich der Größen ξ/r' und η/r' bzw. ξ/s' und η/s' (Abb. 2) entwickelt, wobei ξ und η die Koordinaten des Integrationspunktes in der Öffnung bedeuten. Des weiteren kann der Richtungsfaktor in (6) bei der Integration in guter Näherung als konstant angesehen werden. Schließlich kann noch durch Hinzufügen einer (i.a. komplexen) Transparenzfunktion T(ξ,η) die Wirkung einer in der Öffnung befindlichen, örtlich unterschiedlich absorbierenden und/oder die Phase des Lichtes verändernden Platte erfaßt werden. Bei Beschränkung auf die in ξ und η linearen Terme erhält man so aus (6) die Formel für die Fraunhofersche Beugung


(7)

mit p=x/s'+x₀/r'=l-l₀ und q=y/s'+y₀/r'=m-m₀, wobei l, m die Richtungskosinus des gebeugten Strahles O→P gegen die ξ- und η-Achse, l₀, m₀ die entsprechenden Richtungskosinus des einfallenden Strahles P₀→O und C eine komplexe Konstante bedeuten. Setzt man die Funktion T(ξ,η) durch die Maßgabe T(ξ, η)=0 für die Punkte außerhalb der Öffnung in die ξ-η-Ebene fort, so ist U(kp, kq) die Fourier-Transformierte von T(ξ, η) und umgekehrt. Liegt Rotationssymmetrie vor und gilt T(ξ, η)=T(ρ) mit ρ²=ξ²+η², so kann die Winkelintegration in (7) ausgeführt werden. Das Ergebnis lautet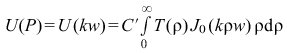


(8)

mit

als dem Sinus des Winkels, den die Beugungsrichtung O→P mit der Richtung des einfallenden Strahles P₀→O (Abb. 2) einschließt. Dabei bezeichnet J₀ die Besselsche Funktion nullter Ordnung und C' eine Konstante. (7) stellt die Hankel-Transformation der Ordnung 0 oder Fourier-Bessel-Transformation dar. Ihre Umkehrung, die inverse Hankel-Transformation, lautet


. (9)

Die Fraunhofersche Näherung gilt im Fernfeld, genauer, wenn r' und s' groß gegen das durch λ geteilte Quadrat der Querdimension der Öffnung sind, was einer Fresnel-ZahlN

1 entspricht. Diese Näherung trifft auch dann zu, wenn Lichtquelle oder Beugungsbild durch Kollimatoren aus dem Unendlichen in die entsprechende Brennebene gerückt werden. Viele praktisch interessierende Fälle liegen im Gültigkeitbereich der Fraunhoferschen Näherung (Beugungserscheinungen).

Man spricht von Fresnelscher Beugung, wenn bei der Entwicklung von r und s im Exponenten der e-Funktion in (6) die in ξ, η quadratischen Glieder berücksichtigt werden. Verallgemeinert man (6) in der Weise, daß man die einfallende Kugelwelle in der Öffnung durch eine allgemeine Feldverteilung U(ξ,η) ersetzt, die entweder einer einfallenden Welle entspricht oder durch die Modifikation einer einfallenden Welle mittels einer Transparenzfunktion T(ξ,η) zustande kommt, so ist nur eine Entwicklung von s erforderlich, und die Feldverteilung U(x,y,z) in der Entfernung vom Schirm ergibt sich zu


(10)

Der Übergang von U(ξ,η) zu U(x,y,z) wird als Fresnel-Transformation bezeichnet. Mit der Fresnelschen Näherung der B. wird beispielsweise die Intensitätsverteilung des gebeugten Lichtes längs der Symmetrieachse einer kreisförmigen Öffnung berechnet und die Beugung an der Halbebene behandelt (Beugungserscheinungen). Weiter spielt die Fresnel-Transformation für die Durchrechnung der Feldverteilung oder auch der Korrelationsfunktion der Felder bei partieller Kohärenz durch optische Systeme hindurch eine große Rolle, insbesondere bei Gaußschen Bündeln. Bei letzteren wird dann oft die Öffnung als unendlich ausgedehnt angenommen.

Die Methode für stationären Phase bzw. die Sattelpunkt-Methode für zweidimensionale Integrale (P. Debye 1909) wird in der B. erfolgreich zur näherungsweisen Berechnung von Integralen des Typs (6) eingesetzt. Sie beruht darauf, daß sich die Phase des Integranden (der Exponent der e-Funktion) bei Bewegung des Integrationspunktes über die Öffnung normalerweise schnell ändert, so daß sowohl der Real- als auch der Imaginärteil des Integranden häufig das Vorzeichen wechseln. Bei Ausführung der Integration heben sich somit die einzelnen Beiträge genähert auf. Wesentliche Beiträge zum Integral kommen daher nur von der Umgebung sogenannter kritischer Punkte oder Pole, an denen die Phase stationär ist, d.h. bezüglich der Lage im Integrationsgebiet ein relatives Maximum oder Minimum aufweist, und in deren Nachbarschaft sich die Phase demzufolge nur schwach ändert. Die resultierenden analytischen Ausdrücke erlauben oftmals eine einfache physikalische Deutung, beispielsweise die wellenoptische Begründung für den Verlauf eines geometrisch-optischen Strahles.

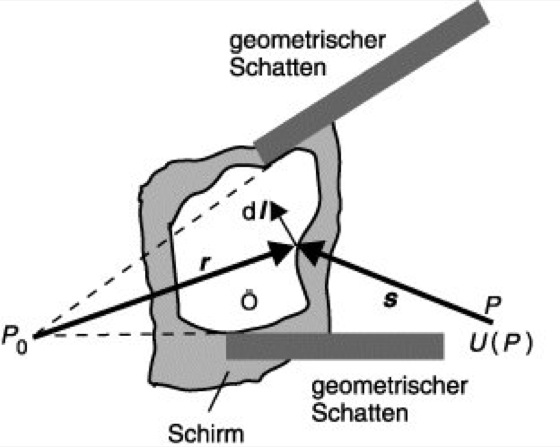
2) Youngsche B. Nach der Youngschen B. ist die vom Rande der Öffnung ausgehende Welle mit dem ungestörten Felde zu überlagern. In Abb. 3 stellt P₀ den Ort der punktförmigen Lichtquelle dar, P den Aufpunkt, wo U(P) gefragt ist, und dl das vektorielle Linienelement auf dem Rande der beugenden Öffnung Ö. Dann ist die Erregung U(P) die Summe der Erregungen der einfallenden Welle, die aber im geometrischen Schattenraume gleich Null gesetzt wird (Sprung an der Schattengrenze) und einer vom Rande der beugenden Öffnung ausgesandten Welle


. (11)

Diese Lösung des Beugungsproblemes ergibt sich aus einer Umformung des Kirchhoffschen Beugungsintegrals (Rubinowicz). Wesentliche Beiträge zum Linienintegral (11) liefern nur Umgebungen solcher Punkte, an denen die durch den Exponenten der e-Funktion ausgedrückte Phase stationär ist (s.o.). Auch im Experiment kann ein besonderes Aufleuchten von bestimmten Teilen des Randes bei Beugung beobachtet werden. Die (5) entsprechende Verallgemeinerung von (11) auf den Fall nichtmonochromatischer Strahlung lautet


(12)

In Fraunhoferscher Näherung von (11), die analog zu (7) mit T=1 ist, ergibt sich für den Fall einer von einem Polygon begrenzten Öffnung leicht die Aussage, daß das Licht vorzugsweise in den zu den einzelnen Polygonseiten senkrechten Richtungen gebeugt wird (Beugungslinien).

3) Parabolische Näherung der Wellengleichung. Dieses auch Näherung der transveralen Diffusion genannte Verfahren wurde von M. Leontovic 1944 und V. Fock 1945 entwickelt. Danach kann sich die Energie infolge Beugung quer zu den Wellenfronten diffusionsähnlich ausbreiten. Wenn sich eine Welle längs der z-Richtung in der Form U=

(x, y, z)exp{i(kz-ωt)} ausbreitet, so setzt man eine langsam veränderliche Amplitude

bezüglich z voraus und vernachlässigt in der Wellengleichung die zweite Ableitung von

nach z. Dann ergibt sich für

die Gleichung


, (13)

die vom Typ der Diffusionsgleichung ist und Lösungen aufweist, die der Fresnel-Beugung (10) entsprechen. Anwendungen findet die parabolische Näherung bei Laserresonatoren, Wellenleitern sowie bei der Ausbreitung von Licht (Strahlmatrix) in linearen und nichtlinearen Medien. Dem numerischen Verfahren der sogenannten BPM (Abk. für engl. beam propagation method) für Lichtausbreitung (besonders in optischen Wellenleitern) liegt ebenfalls die parabolische Näherung zugrunde.

In der geometrischen B. (J. B. Keller 1953) werden die nach dem Fermatschen Prinzip am Schirmrande "gebeugten Strahlen" zwischen Quell- und Aufpunkt mit entsprechenden Phasen addiert. Asymptotische Verfahren, bei denen nach λ/(2πa) mit a als charakteristischer Abmessung des beugenden Körpers entwickelt wird, liefern Zusätze zur geometrischen Optik.

4) Rayleigh-Sommerfeld-Debyesche B. Diese geht statt von Kugelwellen von ebenen Wellen als den zu überlagernden Elementarlösungen der Wellengleichung aus: Wenn man aus der Feldverteilung U(x, y, 0) in der Ebene des Beugungsschirmes (Quellebene) die Feldverteilung U(x, y, z) in der im Abstande z vom Schirm befindlichen Beobachtungsebene berechnen will, so stelle man die Verteilung U(x, y, 0) als Fourier-Integral


(14)

mit dem Ortsfrequenzspektrum

(ν, μ, 0) dar, fasse den Integranden als Verteilung der Randwerte für sich entsprechend der Wellengleichung ausbreitende ebene Wellen

auf und addiere diese Wellen in der Beobachtungsebene zur gesuchten Feldverteilung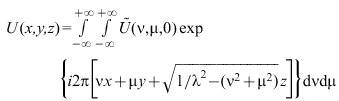


(15)

Positive Radikanden (1/λ²>ν²+μ², reeller Wellenzahlvektor) entsprechen den üblichen ebenen Wellen, während negative Radikanden (1/λ²< ν²+μ², imaginäre z-Komponente des Wellenzahlvektors, Dämpfung längs z) zu quergedämpften Wellen (inhomogene Wellen, Subwellen, engl. evanescent waves) führen, die quer zu ihrer Ausbreitungsrichtung in der x,y-Ebene gedämpft sind, eine Phasengeschwindigkeit kleiner als c besitzen und in einer Entfernung von wenigen Wellenlängen von der Quellebene nur noch geringe Beiträge zum Feld liefern. Die schnelle Dämpfung der quergedämpften Wellen hat zur Folge: 1.Feinheiten der beugenden Struktur, die von geringerer Ausdehnung als λ sind und somit Ortsfrequenzen >1/λ entsprechen, sind in diesen Wellen enthalten und gehen bei Ausbreitung innerhalb weniger Wellenlängen schnell verloren. Die Überwindung der optischen Auflösungsgrenze in der Größenordnung λ beim optischen Nahfeldmikroskop erfordert die Ausnutzung der in den Subwellen enthaltenen Informationen. 2. Das inverse Problem der Bestimmung der Feldverteilung in der Quellebene aus der Feldverteilung in der Beobachtungsebene ist inkorrekt gestellt wegen des exponentiellen Anwachsens der rückwärts zu verfolgenden Subwellen. So können kleine Variationen in der letzteren Verteilung zu sehr großen Änderungen in der ersteren führen. Anwendungen findet die Rayleigh-Sommerfeld-Debyesche Formulierung der B. bei den Debye-Picht-Luneburg-Formeln für konvergierende Wellenfronten, bei systemtheoretischen Untersuchungen von Beugungsproblemen sowie in der Theorie der partiellen Kohärenz.

5) Strenge Beugungstheorien. Hier versucht man, das zeitfreie System der Maxwellschen Gleichungen oder auch die zeitfreie Wellengleichung (Helmholtz-Gleichung) für das elektrische Feld


(16)

und ebenso die für das magnetische Feld H im gesamten Raume einschließlich der beugenden Körper zu lösen, wobei k²(r) stückweise konstant ist. (15) wird noch ergänzt durch die Vorgabe der einfallenden Welle, die Sommerfeldsche Ausstrahlungsbedingung und die Übergangsbedingungen für E und H zwischen verschiedenen Medien, die im Raume verteilt sind. Wurde die Bezeichnung strenge Lösung zunächst für analytische Lösungen der Maxwellschen Gleichungen benutzt, so werden inzwischen numerische Lösungen hoher Genauigkeit mitunter als streng im Sinne von exakt bezeichnet. Der Begriff rigorose B. wird manchmal gebraucht, um zu betonen, daß der Vektorcharakter des Lichtes im Gegensatz zur skalaren B. berücksichtigt wird. Die Anforderungen an die Approximationsgenauigkeit schwanken dabei beträchtlich, allerdings wird manchmal rigoros auch mit streng gleichgesetzt. Eine oft verwendete Idealisierung ist das Modell der unendlichen Leitfähigkeit für die beugenden Körper, das für Metalle im IR-Bereich eine gute Approximation darstellt. Es treten Randwertprobleme auf, wobei die Tangentialkomponenten von E und H auf der Metalloberfläche gleich Null zu setzen sind. Es ergeben sich im allgemeinen Integralgleichungen und Integralgleichungssysteme, die berücksichtigen, daß die in einem Oberflächenelemente eines Körpers erregte Welle nicht nur abgestrahlt wird, sondern auch noch andere Oberflächenelemente beeinflussen kann. Die erste strenge analytische Lösung des Beugungsproblems gelang A. Sommerfeld 1894 für die Beugung an der spiegelnden (unendlich gut leitenden) unendlich dünnen Halbebene. Es ergibt sich im gesamten Raume eine unter anderem die Fresnelschen Integrale enthaltende analytische Lösung für das Feld, die die Kantenbeugung exakt beschreibt. Ähnlich wurden das Problem eines Dipols über einer Halbebene, zwei Halbebenen u.a. behandelt.

Beugungsprobleme mit endlicher Leitfähigkeit der beugenden Körper führen ebenfalls auf Integralgleichungen oder Systeme von Integralgleichungen, wobei Ansätze mit (gesuchten) Monopol- und Dipolschichten die Übergangsbedingungen zwischen den homogenen Gebieten erfüllen müssen. In konkreten Fällen werden die Integralgleichungen mit Rechnern gelöst.

Eine Methode zur Behandlung von allgemeinen Beugungsproblemen besteht darin, solche krummlinigen Koordinaten einzuführen, daß die Oberfläche des beugenden Körpers mit einer Koordinatenfläche zusammenfällt. In den neuen Koordinaten ist zuweilen eine Separation möglich, zuweilen ergeben sich auch numerisch effektivere Verfahren. Räumlich diskretisierende numerische Verfahren wie Finite-Elemente-Methoden oder Finite-Differenzen-Methoden werden in zunehmendem Maße auf die Beugung an komplizierten Strukturen angewandt, um die für die technischen Erfordernisse notwendige Modellierungsgenauigkeit zu erreichen. Neue Wirkprinzipien indessen werden zumeist aus der sinnvollen Verknüpfung der Grunderscheinungen der Optik miteinander gefunden.

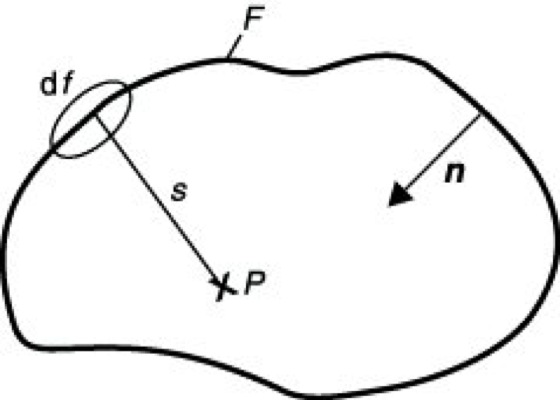
Beugungstheorie 1: Zur Helmholtz-Kirchhoffschen Beugungsformel. Die Lichterregung U und ihre Ableitung

sind auf der Fläche F gegeben.

Beugungstheorie 2: Zur Fresnel-Kirchhoffschen-Beugungsformel. Die Integration erstreckt sich über die Öffnung Ö im Schirm.

Beugungstheorie 3: Zur Randwelle der Beugung.