Brechzahlbestimmung, die Ermittlung der Brechzahl (Brechungsindex) eines Körpers mit Hilfe spektrometrischer, refraktometrischer, interferometrischer, Immersions- und ellipsometrischer Methoden. Daneben gibt es spezielle Methoden zur Messung von Brechzahlprofilen.

1) Spektrometrische B. Der Prüfkörper hat hier in der Regel eine Prismenform mit zwei polierten Planflächen, die sich in der brechenden Kante unter dem Winkel ϕ schneiden. Flüssigkeiten und Gase werden in ebenso gestaltete Hohlprismen eingeschlossen. Bei der Durchstrahlung des Prismas mit Licht wird dieses abgelenkt, so daß zwischen dem eintretenden und dem austretenden Strahl ein bestimmter Ablenkwinkel δ auftritt (Abb. 1). Dieser hängt vom Einfallswinkel α, dem Prismenwinkel ϕ und der zu bestimmenden Brechzahl n des Prismas ab. Bei der spektrometrischen Messung wird das Prisma in einen parallelen Strahlengang gestellt, der senkrecht zur brechenden Kante verläuft. Besonders einfache Verhältnisse erhält man bei senkrechtem Lichteintritt in das Meßprisma. Die Brechzahl n kann dann aus der Beziehung n=sin(ϕ+δ)/sinϕ bestimmt werden. Der Prismenwinkel ϕ muß dabei aber der Bedingung ϕn) genügen.

Allgemein läßt sich die Brechzahl n nach verschiedenen Verfahren aus dem brechenden Winkel ϕ, dem Ablenkwinkel δ oder dem Austrittswinkel β bestimmen (Abb. 1). Zur Messung der Winkel wird ein Spektrometer verwendet. Das Prisma wird dabei auf dem Spektrometertisch zentriert. Zur Bestimmung des brechenden Winkels ϕ (Prismenwinkel) beobachtet man nacheinander eine Reflexion an den beiden Planflächen des Prismas. Dazu werden Kollimator und Fernrohr in einen möglichst spitzen Winkel gestellt, und das Prisma wird so lange gedreht, bis das Kollimatorkreuz mit der Strichmarke im Fernrohre zur Deckung gelangt. Die Differenz der (am Teilkreis abzulesenden) Einstellwinkel für die beiden Prismenflächen ergibt dann 180°±ϕ.

Von den Verfahren zur Ermittlung des Ablenkwinkels δ ist die Methode der Minimalablenkung (nach J. v. Fraunhofer) am gebräuchlichsten (Minimum der Ablenkung). Zur Messung wird die brechende Kante parallel zur Drehachse gestellt. Man beobachtet das Spaltbild des Kollimators im Fernrohre bei Drehung des Prismas so lange, bis sich das Spaltbild immer nach einer Seite bewegt, ganz gleich, ob man das Prisma nach rechts oder links dreht, und liest den Winkel δ ab.

Bei Verwendung von monochromatischem Licht der Wellenlänge λ erhält man dann die Brechzahl nλ für diese Wellenlänge (Minimum der Ablenkung).

Die erreichbare Genauigkeit hängt dabei in erster Linie vom verwendeten Goniometer und von der zu messenden Brechzahl n ab. Man kann mit dieser Methode die Brechzahl mit einer Genauigkeit von Δn = 10^-5 bestimmen, wenn man ein Goniometer mit einer Winkelgenauigkeit Δf≤2″ benutzt und das Prisma die Brechzahl n=1,5 und einen brechenden Winkel von ϕ=60° hat.

2) Refraktometrische B. Sie beruht auf der Messung des Grenzwinkels der Totalreflexion, die an der (ebenen) Grenzfläche zwischen dem Prüfling und einem Meßprisma auftritt. Die Brechzahl n_P des Prismas muß dabei größer als die des Prüflings sein. Mit dem gemessenen Grenzwinkel ψ_G erhält man die Brechzahl n des Prüflings aus der Beziehung n=n_Psinψ_G. Die zur Messung verwendeten Geräte heißen Refraktometer.

Der Grenzwinkel ψ_G kann mit folgenden Verfahren bestimmt werden:

a) Methode des streifenden Eintritts. Der auf das Meßprisma aufgelegte Prüfling wird derart beleuchtet, daß auch Strahlen parallel zur Auflagefläche auftreten. Diese Strahlen wie auch die benachbarten, schräg aus dem Prüfling auf die Auflagefläche treffenden Strahlen werden in das Meßprisma hinein gebrochen, so daß im Meßprisma ein beleuchteter Winkelbereich entsteht, der scharf gegen einen völlig unbeleuchteten Bereich abgegrenzt ist (Abb. 2). Auf diese scharfe Begrenzungslinie (Grenzlinie der Totalreflexion) wird das Fadenkreuz eines schwenkbaren Fernrohres eingestellt und so der Grenzwinkel ψ_G bestimmt.

b) Methode des streifenden Austritts. Es wird der Grenzwinkel der Totalreflexion in Reflexion gemessen. Man läßt Licht unter verschiedenen Einfallswinkeln durch das Meßprisma hindurch auf die Grenzfläche des Prüflings fallen und beobachtet das reflektierte Licht im Fernrohr. Das Gesichtsfeld ist in ein helles und ein weniger helles Feld unterteilt, wobei die Grenze zwischen den Feldern den Grenzwinkel der Totalreflexion darstellt. Um eine scharfe Trennlinie zu erhalten, arbeitet man mit monochromatischem Licht. Man erhält so die Brechzahl für die entsprechende Wellenlänge λ. Bei weißem Licht benutzt man einen Kompensator.

Zur Messung benötigt man nur geringe Mengen an Flüssigkeiten. Bei der Messung an festen Körpern wird zwischen Meßprisma und Prüfkörper eine Immersionsflüssigkeit mit höherer Brechzahl, wie z.B. Bromnaphtalin (n=1,66) eingebracht.

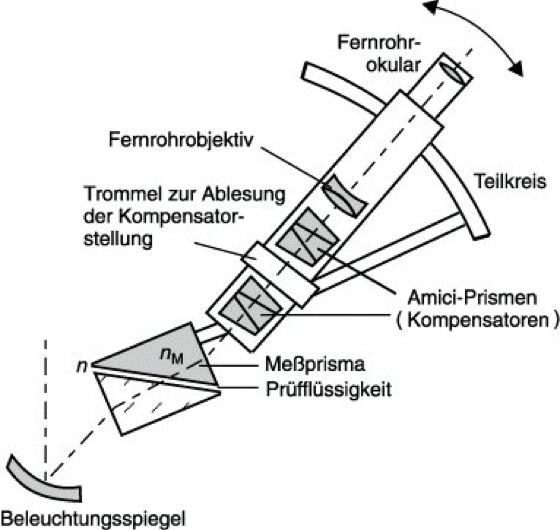
Beim Abbe-Refraktometer (Abb. 3) wird im durchfallenden, weißen Licht beobachtet. Die Prüfflüssigkeit wird zwischen das Beleuchtungs- und das Meßprisma gebracht, die zusammen ein Doppelprisma bilden. Dieses kann gegen das Fernrohr mit dem Teilkreis meßbar gedreht werden. Die geradsichtigen Amici-Prismen lassen sich gegeneinander drehen, wodurch die Dispersion des weißen Lichtes kompensiert werden kann. Die Drehstellung wird von der Trommel angezeigt. Im Gesichtsfelde erscheint eine scharfe Grenzlinie. Am Teilkreise kann dann die Brechzahl für die Na-D-Linie abgelesen werden. Die Meßgenauigkeit beträgt Δn≈2·10^-4. Mit den Werten des Teilkreises und der Trommelstellung kann die mittlere Dispersion n_F-n_C (F-Linie, λ=486,1 nm (blau); C-Linie, λ=656,3 nm (rot)) ermittelt werden. Mit dem Gerät lassen sich aber auch feste Körper untersuchen.

Mit gewissen Abänderungen werden Geräte nach dem Prinzip des Abbe-Refraktometers auch als Butter-, Zucker- oder als Eintauchrefraktometer, ihrem speziellen Einsatzzweck entsprechend, bezeichnet. Beim Pulfrich-Refraktometer wird dagegen die Messung im durchgehenden Licht bei streifendem Einfall durchgeführt (Abb. 4). Es wird mit monochromatischen Licht gearbeitet. Das Ablesefernrohr ist mit einem Teilkreis fest verbunden. Dispersionsmessungen lassen sich so mit hoher Genauigkeit (einige Einheiten in der 5. Dezimale) durchführen.

Meßprismen können auch als drehbare Halbkugeln ausgebildet werden, was sich besonders bei der Untersuchung von Kristallen bewährt hat. Es können somit die von der Orientierung abhängigen Brechzahlen von Kristallen gemessen werden, ohne daß eine Drehung des Kristalles gegenüber der Unterlage erforderlich ist. Das Fernrohr besitzt eine Kompensationslinse zum Ausgleich der Linsenwirkung der Halbkugel. Die Schwenkachse des Fernrohres sowie die Drehachse der Halbkugel müssen dabei durch den Kugelmittelpunkt gehen. Beobachtet wird entweder bei streifendem Einfall des Lichtes oder in Totalreflexion (Meßgenauigkeit: 4. Dezimale). Das nach diesem Prinzip arbeitende Löwesche Taschenrefraktometer mit einem schwenkbaren Mikroskop wird von Juwelieren zur Bestimmung von Edel- und Halbedelsteinen benutzt.

Brechzahlen von Flüssigkeiten können auch mit linsenförmigen Hohlkörpern ermittelt werden. Diese Methode beruht darauf, daß die Brennweite der Linse außer vom Krümmungsradius auch von der Brechzahl der eingefüllten Flüssigkeit abhängt.

3) Interferometrische B. Hierbei werden Gangunterschiede, also Differenzen von optischen Weglängen ns (n Brechzahl, s geometrische Weglänge) gemessen. Diese ändern sich bei einer Änderung der Brechzahl, und damit verschieben sich die Interferenzstreifen. Die Streifenverschiebung wird dabei in Einheiten des Streifenabstandes gezählt. Man verfügt damit über eine sehr empfindliche Methode zur Bestimmung kleiner Brechzahlen oder geringer Brechzahländerungen.

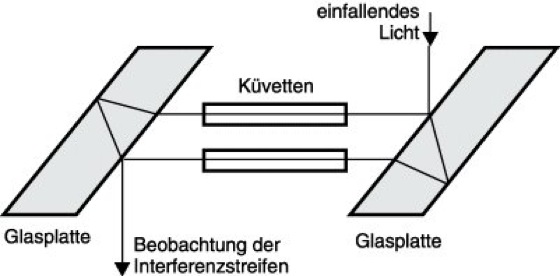
Als Interferometer wird häufig ein Jamin-Interferometer (Abb. 5) benutzt, das zur Strahlenteilung zwei parallele justierbare Glasplatten verwendet, die in einigem Abstand voneinander angeordnet sind. Bringt man zwei optisch gleiche Körper wie z.B. zwei mit Gas gefüllte Rohre gleicher Länge s in die beiden Strahlengänge und verändert den Druck oder die Temperatur des Gases in einem der Rohre, dann erkennt man mit einem Beobachtungsfernrohr eine Verschiebung der Interferenzstreifen. Diese Streifenverschiebung Z (in Einheiten des Streifenabstandes) ist dann ein Maß für die Brechzahländerung des Gases. Bei bekannter Wellenlänge λ ergibt sich die Brechzahländerung Δn aus der Beziehung Δn =Zλ/s. Den Abstand der Interferenzstreifen kann man vor der Messung durch eine geringe Neigung der Platten gegeneinander einstellen.

Beim Mach-Zehnder-Interferometer, bei dem die Strahlenteilung und -vereinigung wie beim Jamin-Interferometer erfolgt, erreicht man durch Einfügen von zwei Spiegeln einen größeren Abstand der Teilstrahlenbündel, wodurch auch größere Untersuchungsgegenstände in den Strahlengang gebracht werden können. Dieses Interferometer wird in Verbindung mit einem Mikroskop z.B. auch zur Bestimmung von Brechzahlprofilen von optischen Fasern eingesetzt. Man bringt dazu ein auf beiden Seiten poliertes Faserstück mit ebenen Oberflächen in den Strahlengang des Interferometers (in Transmission oder Reflexion) und beobachtet den Verlauf der Interferenzstreifen. Der Brechungsindexverlauf kann dann aus der Verschiebung der Interferenzstreifen des Mantels gegenüber denen des Faserkerns ermittelt werden. Die Methode erfordert aber einen relativ großen Aufwand zur Präperation der Faserscheibchen.

Für genaue Gas- und Flüssigkeitsanalysen benutzt man auch das Interferometer nach Rayleigh-Haber-Löwe. Hier werden die kohärenten Lichtbündel durch eine Doppelblende aus dem vom Kollimator kommenden Licht ausgeblendet. Nach dem Durchlaufen der Küvetten und des Kompensators werden sie in der Brennebene eines Objektivs vereinigt, wo die Interferenzstreifen beobachtet werden können. Durch den Kompensator kann der durch den Probekörper verursachte Gangunterschied wieder aufgehoben werden. Zwei Lichtbündelpaare unterhalb der Küvetten liefern ein Bezugssystem. Bei entsprechend langen Gasküvetten lassen sich so Brechzahldifferenzen von Δn=±10^-8 messen.

Zur B. lassen sich auch spezielle Interferometeranordnungen, wie z.B. solche auf der Basis von Fizeauschen Doppelplatten verwenden. Mit der ersten Platte erzeugt man zwei parallele, kohärente Bündel, die dann die Meßküvetten durchlaufen und mit einer zweiten Doppelplatte wieder vereinigt werden. Beim Interferometer nach Michelson und Kinder (Abb. 6) werden die kohärenten Strahlenbündel durch Teilung an den Spiegelflächen eines planparallelen Prismas erzeugt. Ähnlich wie beim Interferometer nach Rayleigh-Haber-Löwe arbeitet man mit einem Kompensator und erzeugt zusätzlich ein Bezugsinterferenzbild.

Eine B. kann auch mit dem Interferenzmikroskop vorgenommen werden.

4) Immersionsmethoden. Bettet man einen Körper in eine Flüssigkeit ein, so zeigen sich die Konturen des Körpers um so deutlicher, je größer der Brechzahlunterschied zwischen Flüssigkeit und Körper ist. Ändert man nun die Brechzahl der Flüssigkeit so, daß sie der des Körpers näher kommt, werden die Körperkonturen schwächer und bei Angleichung beider Brechzahlen verschwinden sie völlig, wenn der Prüfkörper die gleiche Farbe wie die ihn umgebende Flüssigkeit hat. Man mischt dazu meist Immersionsflüssigkeiten bekannter Brechzahl zur Anpassung an die Brechzahl des Prüfkörpers. Bei Übereinstimmung kann dann die Brechzahl der Immersionsflüssigkeit mit dem Refraktometer bestimmt werden. Mit diesem Verfahren kann man z.B. die Brechzahl von mikroskopisch kleinen Körnern (Kristallkörner, Pulver) unter dem Mikroskop bestimmen. An den in der Immersionsflüssigkeit befindlichen Körpern tritt bei Beleuchtung ein heller Lichtsaum, die Becke-Linie auf, solange sich die Brechzahlen von Immersion und Körnern unterscheidet. Bei Gleichheit der Brechzahlen verschwindet diese Linie. Eine Angleichung geringer Brechzahlunterschiede kann bei dieser Methode auch durch Variation der Temperatur der Probe oder durch Änderung der Lichtwellenlänge erfolgen. Die Feststellung der Übereinstimmung kann z.B. mit einem Schlierengerät erfolgen.

Immersionsmethoden werden auch in Verbindung mit der Interferenzmikroskopie zur Untersuchung kleiner Objekte angewendet. Die Prüfkörper bekannter Dicke d werden dazu in eine Immersion mit bekannter Brechzahl n_I eingebettet (Tab.). Im Interferenzmikroskop wird dann der Gangunterschied Δl zwischen der Probe und der Immersionsflüssigkeit bestimmt. Die Brechzahl n des Prüfkörpers kann dann nach folgender Formel ermittelt werden: n=n_I+Δl/d.

5) Ellipsometrische B. In der Ellipsometrie wird neben dem Realteil des Brechungsindexes (Brechzahl) auch dessen Imaginärteil (spektrale Absorptionszahl) bestimmt.

6) Messung von Brechzahlprofilen. Neben den erwähnten interferometrischen Verfahren zur Bestimmung von Brechzahlprofilen werden vor allem bei optischen Fasern auch Nahfeld-Scanning- und Reflexionsverfahren angewendet. Die Differenz der Brechzahlen von Kern und Mantel liegt bei etwa 1% bis 1‰.

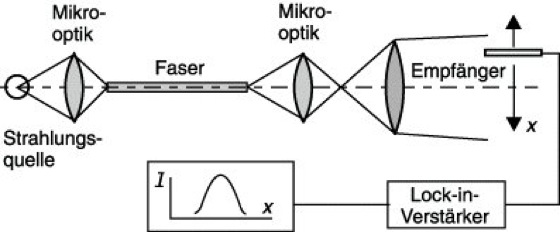
Bei der Nahfeld-Scanning-Methode (Abb. 7) geht man davon aus, daß zwischen der Intensitätsverteilung im Nahfeld einer beleuchteten Faser und der Brechzahlverteilung der Faser ein eindeutiger Zusammenhang existiert, wenn die Faser (Länge größer als 1 m) mit einem Lambert-Strahler zur Anregung aller geführten Moden beleuchtet wird. Das optisch vergrößerte Bild des Faserausganges wird mit einem empfindlichen Empfänger kleiner Fläche (z.B. Si-pin-Diode) senkrecht zur Faserachse abgetastet. Aus der so erhaltenen Intensitätsverteilung I(r) (r Abstand von der Kernachse) kann die Brechzahlverteilung n(r) dann aus einer relativ einfachen Beziehung berechnet werden.

Die Bestimmung von Brechzahlprofilen aus der Fernfeldverteilung erfordert dagegen eine komplexe Analyse sowohl der vorwärts auch als der rückwärts gestreuten Intensität.

Brechzahlprofile von Fasern können aber auch durch mikroskopische Reflexionsmessungen bestimmt werden. So ergibt sich nach den Fresnelschen Formeln für senkrechten Lichteinfall das Verhältnis der Intensität des von der Grenzfläche Glas-Luft reflektierten Lichtes (I_R) zu der des auffallenden Lichtes (I₀) zu:


,

wobei n der Brechungsindex an einem bestimmten Punkte der Faseroberfläche ist. Mit entwickelten Methoden kann eine Genauigkeit der B. erreicht werden, die besser als 10^-3 ist.

Brechzahlbestimmung 1: Spektrometrische Bestimmung der Brechzahl n.

Brechzahlbestimmung 2: Brechzahlmessung bei streifendem Eintritt mit einem Halbkugelrefraktometer. n Brechzahl.

Brechzahlbestimmung 3: Abbe-Refraktometer. n_M und n Brechzahl des Meßprismas und des Prüflings.

Brechzahlbestimmung 4: Meßprisma des Pulfrich-Refraktometers bei Beleuchtung mit streifendem Einfall. n Brechzahl.

Brechzahlbestimmung 5: Brechzahlmessung mit einem Jamin-Interferometer.

Brechzahlbestimmung 6: Brechzahlmessung mit einem Interferometer nach Michelson und Kinder.

Brechzahlbestimmung 7: Nahfeld-Scanning-Methode zur Bestimmung von Brechzahlprofilen von Lichtleitfasern. I Intensität.