Debye-Picht-Luneburg-Formeln für konvergierende Wellenfronten. Im Rahmen der Formulierung der Beugungstheorie mit Hilfe von Überlagerungen ebener Wellen kann die Fokussierung aberrationsfreier wie auch aberrationsbehafteter konvergierender Wellenfronten für Abbildungszwecke behandelt werden. Die allgemeine Superposition monochromatischer ebener Wellen unterschiedlicher, durch einen Einheitsvektor e gekennzeichneter Ausbreitungsrichtung mit einer Gewichtsfunktion ϕ(v, w)


(1)

wobei k die Wellenzahl bezeichnet, ist eine Lösung der Helmholtz-Gleichung (E. T. Whittaker 1903). Speziell läßt sich ein durch eine Blende ausgeschnittener Teil einer einlaufenden (also konvergierenden) Kugelwelle in beugungstheoretischer Näherung in der Form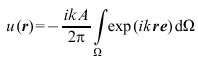


(2)

darstellen (P. Debye 1909). Die Integration erstreckt sich dabei über den Raumwinkel Ω, unter dem die Blende im Wellenzentrum (Fokus) erscheint, und der auf den Fokus gerichtete Einheitsvektor e liegt in der Achse des Raumwinkelelementes dΩ, kennzeichnet also die im einfallenden Lichte vertretenen Ausbreitungsrichtungen. Die Größe A gibt die Amplitude der Kugelwelle in der Blendenöffnung, multipliziert mit dem Abstande der Kugelwelle vom Fokus, an. Anwendungen findet (2) bei der Berechnung des Airy-Scheibchens sowie der Feldverteilungen in der Nähe eines Brennpunktes. (2) läßt sich nach J. Picht (1924) in der Weise verallgemeinern, daß eine unterschiedliche Wichtung der verschiedenen ebenen Wellen mit einem Faktor ψ vorgenommen wird und außerdem von der Kugelwelle abweichend gekrümmte Wellenfronten in Betracht gezogen werden. Man gelangt so zu dem Ergebnis


(3)

Dabei kennzeichnet ψ (v, w) die mit der Entfernung R

λ vom Konvergenzpunkte multiplizierte vorgegebene Amplitudenverteilung, die der weit entfernten geometrisch-optischen Wellenfläche entspricht, W=W(u, w) ist die Darstellung der Wellenfläche des Strahlenbündels als Funktion der Parameter v, w, und n(v, w) bezeichnet den Normalenvektor auf W(u, w), der in die Richtung des von W ausgehenden Lichtstrahles zeigt. Die Beugungsfigur kann also aus der Kenntnis einer beliebigen Wellenfläche des Bündels heraus berechnet werden. Weiter ist es möglich, das durch (3) bestimmte Bündel nicht aus der vorgegebenen Wellenfläche W(u, w), sondern aus der vorgegebenen Kaustikschale K(v, w) (Brennfläche) zu berechnen, weil K die Evolutenfläche von W ist. Für das elektrische Feld E und für das magnetische Feld H sind zu (3) analoge Zerlegungen nach ebenen Wellen von R. K. Luneburg 1944 unter Benutzung des gemischten Eikonals anstelle von W angegeben worden. Anwendung finden die D. bei der Feld- und Intensitätsberechnung im Bildgebiete beliebiger Strahlenbündel, aber auch für Planwellen-Entwicklungen bei allgemeinen Wellenausbreitungsproblemen, beispielsweise der Radiometrie.