Dispersion der optischen Achsen, die Abhängigkeit der Lage der optischen Achsen, d.h. der Binormalen (Kristalloptik), von der Lichtwellenlänge λ bei zweiachsigen Kristallen, zurückzuführen auf die Dispersion der drei Hauptbrechungsindizes. Je nach den Symmetrieeigenschaften der zweiachsigen Kristalle können sich der Winkel zwischen den Binormalen und die Ebene der Binormalen mit λ ändern. Damit ändern sich die Interferenzen in Kristallen im konoskopischen Strahlengange, z.B. senkrecht zur Bisektrix.

In der Abb. stellen die ausgezogenen hyperbelförmigen Kurven die Hauptisogyren der Interferenzfigur für eine erste Wellenlänge und die gestrichelten Hyperbeln die Hauptisogyren für eine zweite Wellenlänge dar. Die entsprechenden ausgezogenen oder gestrichelten geraden Linien sind die Spuren der Binormalenebene. Die Binormalen sind durch ausgefüllte Punkte, die 1. Bisektrix durch einen kleinen Kreis markiert. Ausgezogene Geraden bedeuten zugleich die Spur der senkrecht zur Zeichenebene stehenden Symmetrieebene, und die Pfeile geben die Richtungen zweizähliger Symmetrieachsen an. Folgende Fälle sind möglich: 1) Bei den rhombischen Kristallen sind die Richtungen der optischen Symmetrieachsen unabhängig von der Wellenlänge. Jedoch ist der Achsenwinkel unterschiedlich. In diesem Falle spricht man von symmetrischer Dispersion. 2) Bei den monoklinen Kristallen unterscheidet man die geneigte Dispersion, bei der die Binormalenebene mit der Symmetrieebene zusammenfällt, die gekreuzte Dispersion, bei der die zweizählige Symmetrieachse mit der 1. Bisektrix zusammenfällt und die horizontale Dispersion, bei der die zweizählige Symmetrieachse senkrecht auf der 1. Bisektrix in der Binormalenebene steht. 3) Bei den triklinen Kristallen sind die Lagen der Binormalen für verschiedene Wellenlängen durch kein Symmetrieelement festgelegt (asymmetrische Dispersion).

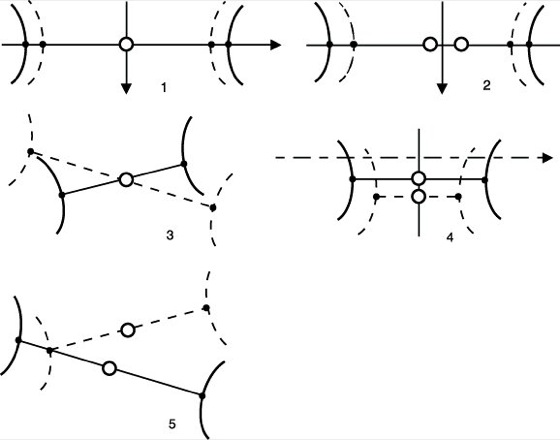
Dispersion der optischen Achsen: 1) symmetrische, 2) geneigte, 3) gekreuzte, 4) horizontale, 5) asymmetrische Dispersion.