Dispersionsprismen, vor allem in Prismenspektralapparaten zur spektralen Zerlegung der zu untersuchenden Strahlung benutzte Prismen. Als Prismenmaterial werden neben Glas unterschiedliche Kristalle, mitunter auch Flüssigkeiten, die in ein dünnwandiges Gefäß mit der gewünschten Prismenform gebracht werden (Flüssigkeitsprismen) verwendet.

Die wichtigsten Typen der D. und Dispersions-Prismen-Systeme sind die folgenden:

1) Geradsichtprismen. Sie stellen im allgemeinen eine Prismenkombination dar, die aus zwei oder mehr Prismen verschiedenen Materials zusammengesetzt ist. Sie bewirken, daß das auf das Prisma auffallende Lichtbündel für eine bestimmte Wellenlänge keine Ablenkung erleidet (beispielsweise bei einem Handspektroskop). Zu den Geradsichtprismen gehört das Amici-Prisma, auch Browning-Prisma genannt (Abb. 1). Es besteht aus einem Flintglasprisma (große Dispersion) und zwei kleineren Kronglasprismen (kleine Dispersion), die auf ersteres aufgekittet sind; oft auch aus zwei (bzw. drei) Flint- und drei (bzw. vier) Kronglasprismen. Die brechenden Winkel werden so gewählt, daß sich für eine bestimmte Wellenlänge keine Ablenkung ergibt. Da sich aber die Dispersionen der einzelnen Prismen für die übrigen Wellenlängen nur teilweise kompensieren, erhält man dennoch ein Spektrum. Da jedoch die Dispersion des Flintglasprismas derjenigen der Kronglasprismen entgegengesetzt ist, sind sowohl die Gesamtdispersion als auch das Auflösungsvermögen des Amici-Prismas relativ klein. Ein weiteres Geradsichtsprisma ist das Zenker-Prisma (Abb. 2), bestehend aus zwei gleich großen Prismen verschiedener Dispersion, die aus Substanzen hergestellt sind, die für eine bestimmte Wellenlänge den gleichen Brechungsindex besitzen. Diese werden dann zu einem Parallelepiped zusammengesetzt. Denkt man sich zwei Zenker-Prismen hintereinander angeordnet, so ergibt sich das Wernicke-Prisma (Abb. 3), das sich durch eine große Winkeldispersion auszeichnet, da für das mittlere Prisma ein großer brechender Winkel (etwa 100°) benutzt werden kann. Das Rutherford-Prisma (Abb. 4), auch Compoundprisma genannt, besteht aus einem Flintglasprisma mit großem brechenden Winkel (meist 90 bis 120°) und zwei gleichen symmetrisch aufgekitteten Kronglasprismen.

2) Prismensysteme mit konstanter Ablenkung. Sie ergeben sich, wenn außer der Brechung noch eine Reflexion an einer mitgedrehten Fläche stattfindet. Das einfachste Prisma dieser Art ist das Autokollimationsprisma (Abb. 5), in der Regel ein 30°-Prisma mit verspiegelter Rückfläche, mitunter auch ein halbes Rutherford-Prisma. Dasjenige Lichtbündel, das diese Spiegelfläche senkrecht trifft, wird in sich reflektiert und erfährt daher eine Ablenkung um 180°. Die diesem zugehörige Wellenlänge kann durch Drehen des Prismas gegenüber der festen Einfallsrichtung beliebig variiert werden. Andere Ablenkungswinkel erhält man mit den Abbe-Prismen. Ein solches Prisma mit einer Ablenkung von 90° zeigt Abb. 6. Es wird mitunter im angelsächsischen Schrifttum auch als Pellin-Broca-Prisma bezeichnet. Es ist eine Kombination aus zwei 30°-Flintglasprismen (Halbprismen) ADD' und DCB (bzw. D'C'B) sowie einem totalreflektierenden 90°-Prisma D'BA. In der Regel wird es aus einem einzigen Glasblock hergestellt. Die Größe des brechenden Winkels der beiden Halbprismen ist nicht in jedem Falle 30°, sondern hängt von der Glasart ab. Durch passende Wahl des Reflexionsprismas können auch andere feste Ablenkungswinkel, z.B. 60° realisiert werden. Ein System, bestehend aus einem Abbe-Prisma und zwei 60°-Prismen, stellt der Försterlingsche Dreiprismensatz dar (Abb. 7). Er liefert eine sehr hohe Auflösung und Dispersion. Da sich die durch die beiden 60°-Prismen erzeugten Ablenkungen gegenseitig aufheben, bleibt nur die konstante Ablenkung des Abbe-Prismas übrig. Um die Auflösung noch weiter zu steigern, kann man den Dreiprismensatz auch in Autokollimation benutzen. Ein anderes System konstanter Ablenkung ist das Wadsworth-Spiegelprisma, auch Fuchs-Wadsworth-Prisma genannt, bei dem ein Prisma auf einen ebenen Spiegel gesetzt ist.

Ein System, das zwar keine konstante Ablenkung besitzt, jedoch in einfacher Weise für eine beliebige Wellenlänge das Minimum der Ablenkung einzustellen gestattet, ist das Young-Prisma (Abb. 8), auch Young-Thollon-Prisma genannt. Es besteht aus zwei Halbprismen P₁ und P₂, die um eine gemeinsame Achse drehbar sind. Mitunter wird als Drehachse eine gemeinsame Kante benutzt (bei 30°-Prismen die 60°-Kante). Wird das Kollimatorrohr mit P₁ und das Fernrohr mit P₂ starr verbunden, so erhält man, wenn das Licht senkrecht auf die erste Prismenfläche auftrifft, stets für diejenige Wellenlänge das Minimum der Ablenkung, deren Lichtstrahlen in der Achse des Fernrohrobjektivs fokussiert werden; vorausgesetzt, daß diese mit der Normalen der letzten Prismenfläche zusammenfällt.

Wird als Prismenmaterial an Stelle eines isotropen Mediums ein anisotropes benutzt, so müssen die richtungsabhängigen optischen Eigenschaften berücksichtigt werden. Verwendet man z.B. kristallinen Quarz, so ist darauf zu achten, daß die durch dessen Doppelbrechung und optische Aktivität möglichen Störungen weitgehend vermieden werden. Einfache Quarzprismen werden so geschliffen, daß die optische Achse des Kristalles zur Basis parallel ist. Da jedoch die für die optische Aktivität verantwortliche Rotationsdoppelbrechung auch in der optischen Achse des Kristalles in Erscheinung tritt, setzt man das Prisma aus zwei Halbprismen zusammen, von denen das eine aus Rechtsquarz und das andere aus Linksquarz hergestellt ist. Es entsteht so das Cornu-Prisma oder Quarz-Cornu-Prisma, bei dem die Rotationsdoppelbrechung des ersten Halbprismas durch diejenige des zweiten aufgehoben wird. Bei einem Autokollimationsprisma geschieht das durch den Hin- und Hergang des Lichtes in demselben Halbprisma. Neben diesen beiden Prismen aus Kristallquarz wird mitunter auch das Straubel-Prisma benutzt, das aus zwei Quarzprismen mit zueinander senkrechten optischen Achsen besteht. Man erhält so im Minimum der Ablenkung, ebenso wie bei den oben behandelten Quarzprismen, keinerlei Doppelbrechung.

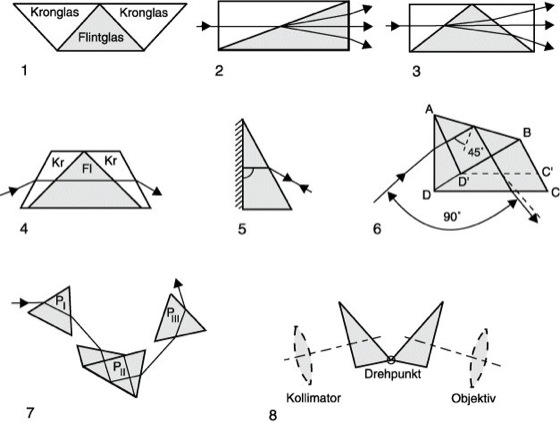
Dispersionsprismen: 1 Amici-Prisma; 2 Zenker-Prisma; 3 Wernicke-Prisma; 4 Rutherford-Prisma, Fl Flintglas, Kr Kronglas; 5 Autokollimationsprisma; 6 Abbe-Prisma mit 90° Ablenkung; 7 Försterlingscher Dreiprismensatz, P_I und P_III gleichseitige Prismen, P_II Abbe-Prisma mit 90° Ablenkung; 8 Young-Prisma.