Eikonal, der ortsabhängige Phasenterm E(x, y, z) einer monochromatischen Welle mit der komplexen Amplitude u=|u|exp(2πiE/λ₀), wobei λ₀ die Vakuumwellenlänge bezeichnet. Die Flächen konstanten E. sind Phasen- und damit Wellenflächen. Das E. gehorcht der Eikonalgleichung (grad E)²=n² (n im allgemeinen ortsabhängige Brechzahl), der zufolge die Lichtstrahlen die Wellennormalen

sind. Die Richtungskosinus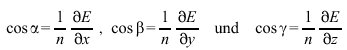

des Einheitsvektors s₀ in Strahlrichtung ergeben sich demnach durch räumliche Ableitung des E. in dem betreffenden Punkte.

Das E. hängt mit der optischen Weglängel in der Form

zusammen.

Als Funktion der Koordinaten der (auf einem Lichtstrahl liegenden) Punkte P und Q geschrieben, wird die optische Weglänge als Punkt- oder Streckeneikonal bezeichnet.

Von großer Bedeutung für die Theorie der optischen Abbildung ist das Schwarzschildsche Winkeleikonal W, das folgendermaßen definiert ist: Man wähle in dem Raumgebiet vor und hinter dem optischen System jeweils einen Bezugspunkt A bzw. A'. Das Winkeleikonal beschreibt dann die optische Weglänge zwischen den Fußpunkten des Lotes von A bzw. A' auf einen betrachteten Lichtstrahl, ausgedrückt durch die Richtungskosinus cosα, cosβ und cosα', cosβ' der Strahlrichtung vor bzw. hinter dem optischen System, W=W(cosα, cosβ; cosα', cosβ'). (cosγ, und entsprechend cosγ', wurden mit Hilfe der Relation cos²α+cos²β+cos²γ=1 eliminiert.) Spezialisiert man sich auf ein zentriertes optisches System und wählt A bzw. A' als den Schnittpunkt der Objekt- bzw. Bildebene mit der optischen Achse, so ergeben die Ableitungen von W nach den Richtungskosinus die Koordinaten x, y und x', y' der Strahldurchstoßpunkte O und O' in der Objekt- und der Bildebene: es gilt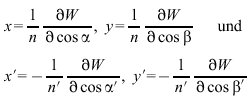

wobei n und n' die als räumlich konstant vorausgesetzten Brechungsindizes im Objekt- und Bildraum bezeichnen.

Besonders vorteilhaft ist es, die Richtungskosinus entsprechend cosα=(x-x_B)/p, cosβ=(y-y_B)/p, cosα'=(x'-x'_B)/p' und cosβ'=(y'-y'_B)/p' zugunsten der Koordinaten der konjugierten Punkte O und O' und der Strahldurchstoßpunkte B(x_B, y_B, z_B) und B'(x

, y

, z

) in der Ein- und Austrittspupille (Blende) sowie der objekt- und bildseitigen Pupillenschnittweiten p und p' zu eliminieren. Man kann dann das so umgeformte Winkeleikonal nach Potenzen der Koordinaten der Bildebene und der Austrittspupille entwickeln, wobei wegen der Axialsymmetrie nur Glieder geradzahliger Ordnung auftreten: W=W₀+W₂+W₄+W₆+... Das Glied 0. Ordnung W₀ entspricht dem axialen Lichtweg von der Objekt- bis zur Bildebene. Das Glied 2. Ordnung W₂ definiert über die paraxialen Objekt- und Bildhöhen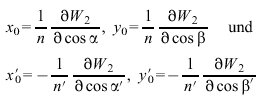

den paraxialen Abbildungsmaßstab. Damit beschreiben W₀ und W₂ die paraxiale Abbildung. Durch das Glied W₄ werden die meridionalen und die sagittalen Queraberrationskomponenten 3. Ordnung


,

die auch als Seidelsche Bildfehler bezeichnet werden, definiert. Alle Glieder höherer Ordnung enthalten entsprechende Bildfehleranteile höherer Ordnung (z.B. die Bildfehler 5. Ordnung). Das E. ist damit die Basis der analytischen Bildfehlertheorie. Die Summe, die man aus der Reihenentwicklung des Winkeleikonals nach Abspaltung der paraxialen Glieder W₀+W₂ erhält, entspricht der Wellenaberration.

Führt man mit Hilfe der Helmholtz-Lagrangeschen Invariante in das auf die Objekt-, Bild- und Pupillenkoordinaten bezogene Winkeleikonal noch abbildungs- und damit maßstabsinvariante Koordinaten ein, erhält man das Seidelsche E., das in einfacher Weise eine Diskussion der analytischen Bildfehler (Aberrationen), auch bei aus mehreren Teilsystemen zusammengesetzten Systemen, gestattet und zu für die Aberrationsberechnung günstigen Formeln führt.