elektrooptische Effekte, die Änderung optischer Eigenschaften von Substanzen durch äußere elektrische Felder. Dazu gehören der Franz-Keldysch-, der Pockels-, der Kerr-, der Stark-Effekt sowie Elektroabsorption und -reflexion.

Als Franz-Keldysch-Effekt (W. Franz, L.W. Keldysch 1958) wird die Änderung der optischen Eigenschaften in der Nähe der Grundgitterabsorptionskante von Halbleitern in einem äußeren elektrischen Feld E bezeichnet. Die Ursache ist, daß bei Anwesenheit eines elektrischen Feldes die Elektronen im Festkörper als Folge von Tunnelprozessen auch Energien in der verbotenen Zone haben können. Die Wahrscheinlichkeit dafür nimmt mit dem energetischen Abstand zu den Bandrändern exponentiell ab, was zu exponentiell abklingenden Ausläufern in der optischen Absorption an der Absorptionskante führt. Bei Halbleitern mit exponentieller Absorptionskante bewirkt der Franz-Keldysch-Effekt eine Verschiebung der Absorptionskante zu kleineren Photonenergien hin, die in erster Näherung proportional zu E² ist. Die Folge davon ist eine Änderung des Absorptionskoeffizienten α bei einer festen Wellenlänge λ in der Nähe der Absorptionskante. So ändert sich α z.B. im Falle von CdS_0,5Se_0,5 bei λ=588 nm um Δα=200/m, wenn E von 0 bis 2500 kV/m anwächst. Infolge seiner geringen Trägheit bietet der Franz-Keldysch-Effekt Möglichkeiten zur Modulation des Lichtes bis zu sehr hohen Frequenzen.

Der Pockels-Effekt (J. Kerr 1875, W.C. Röntgen 1883, F. Pockels 1893) oder lineare elektrooptische Effekt besteht darin, daß in einem Kristall mit fehlendem Inversionszentrum durch Anlegen eines elektrischen Feldes eine linear mit der elektrischen Feldstärke E=(E₁, E₂, E₃) anwachsende optische Doppelbrechung erzeugt bzw. eine bereits vorhandene Doppelbrechung entsprechend geändert wird. Der Pockels-Effekt wird durch die folgende Abänderung der Fletcherschen Indikatrix (Kristalloptik, Gl. (6)) beschrieben: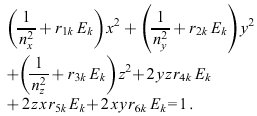


(1)

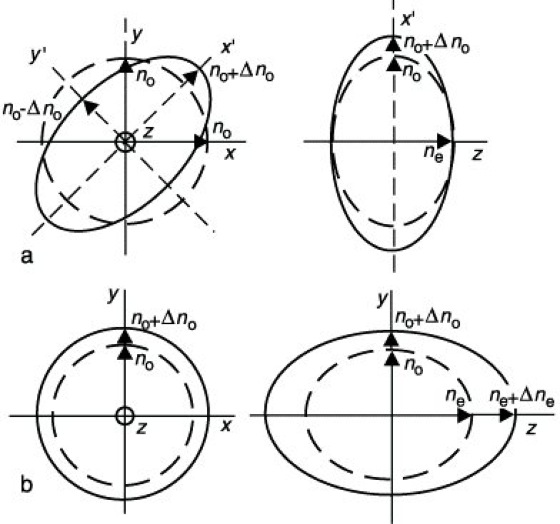
Dabei bezeichnen n_x, n_y und n_z die Hauptbrechungsindizes und die r_ik(i=1, ..., 6; k=1, 2, 3) die elektrooptischen Koeffizienten; über doppelt auftretende Indizes ist zu summieren. Je nach Kristallsystem sind nur bestimmte r_ik von Null verschieden. Einige Werte der elektrooptischen Koeffizienten sind in Tabelle 1 angegeben. Durch Steuern der Komponenten E_k des elektrischen Feldes können die Form und die Lage der Indikatrix geändert und damit die Doppelbrechung eines Kristalls sowie die Polarisation des hindurchgehenden Lichtes verändert werden. Der Pockels-Effekt wird daher zur Modulation des Lichtes verwendet. Die Veränderung der Indikatrix mit E ist in der Abb. dargestellt.

Als elektrooptischen Kerr-Effekt (J. Kerr 1875), quadratischen elektrooptischen Effekt oder elektrische Doppelbrechung bezeichnet man das Auftreten einer mit der elektrischen Feldstärke eines angelegten Feldes quadratisch anwachsenden optischen Doppelbrechung – bzw. einer entsprechenden Änderung einer bereits vorhandenen Doppelbrechung – in einem Medium beliebiger Symmetrie (z.B. Nitrobenzol, Schwefelkohlenstoff). Die Fletchersche Indikatrix (Kristalloptik, Gl. (6)) wird beispielsweise für ein isotropes Medium mit dem Brechungsindex n, das sich in einem äußeren, in z-Richtung liegenden Feld E befindet,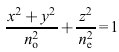


(2)

mit den folgenden Werten des Brechungsindexes für die ordentliche bzw. die außerordentliche Welle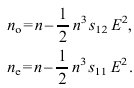

Dabei sind s₁₂, s₁₁ zwei unabhängige von im allgemeinen 36 quadratischen elektrooptischen Koeffizienten s_ik(i, k=1, ..., 6). Wieder ist die Fletchersche Indikatrix durch E steuerbar. Die aus (2) resultierende Doppelbrechung beträgt


(3)

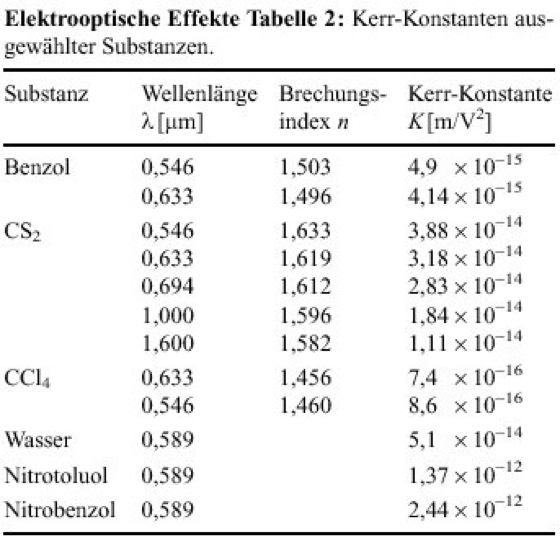
mit der Kerr-Konstanten K und der Vakuumwellenlänge λ des Lichtes. Einige Kerr-Konstanten sind in Tabelle 2 aufgeführt. Anwendung findet der Kerr-Effekt bei der Modulation des Lichtes.

elektrooptische Effekte: Pockels-Effekt. Schnitte durch das Indexellipsoid von a) KDP, ADP und b) LiTaO₃ ohne (---) elektrisches Feld und mit (--) elektrischem Feld in z-Richtung. n_o und n_e Brechungsindex für die ordentliche bzw. die außerordentliche Welle.