Farbmetrik, die Lehre von den Maßbeziehungen für Farben.

1) Die niedere F. oder Farbvalenzmetrik ist die Maßlehre von den Farben, die sich auf dem Gleichheitsurteil über Farben aufbaut. Sie ist die theoretische Grundlage der Farbmessung, ihr liegen die Gesetzmäßigkeiten der additiven Farbmischung zugrunde. Eine Farbvalenz wird als additive Mischung dreier vereinbarter Primärvalenzen durch die erforderlichen Mischungsbeträge beschrieben und kann als Vektor in einem von den Primärvalenzen aufgespannten Vektorraum der Farbvalenzen, dem Farbenraum, dargestellt werden. Zwischen einer Farbvalenz F und drei Primärvalenzen, z.B. R, G, B, gibt es eine eindeutige Zahlenbeziehung in Gestalt einer Farbgleichung F=RR+GG+BB. Die Vektorrichtungen und die Einheitslängen der Primärvalenzen sind beliebig wählbar; die Mischungsbeträge R, G, B sind die Farbwerte der Farbvalenz F bezüglich der Primärvalenzen R, G, B.

Der Übergang von einem Primärvalenztripel zu einem beliebigen anderen wird durch eine affine Transformation (d.h. eine lineare Transformation, die jedem Vektor umkehrbar eindeutig einen anderen Vektor zuordnet) vermittelt, da jede Primärvalenz des einen Satzes durch eine Mischung der Primärvalenzen des anderen Satzes dargestellt werden kann.

Da sich für jede beliebige Farbvalenz F experimentell eine Farbgleichung ermitteln läßt, trifft dies im besonderen für jede spektrale Farbvalenz fλ zu. In den Farbgleichungen für die einzelnen Spektralfarben des energiegleichen Spektrums

(λ Wellenlänge) bezeichnet man die Farbwerte

als Spektralwerte bezüglich der Primärvalenzen R, G, B. Sie ergeben stetige Kurven, die Spektralwertkurven oder -funktionen. Da jeder Farbreiz ϕ als Summe einzelner Spektralbanden der Breite Δλ verstanden werden kann – wobei jedem Spektralband die relative spektrale Strahldichte ϕλ zukommt –, kann jede Farbvalenz F als eine gewichtete Summe (additive Farbmischung) der Farbvalenz fλ der einzelnen Spektralbänder aufgefaßt werden:

. Der Farbwert R der additiven Mischung ergibt sich daraus zu

, und das Analoge gilt für G und B. Ist Δλ hinreichend klein, können statt der Summen Integrale geschrieben werden. Mit Hilfe der Spektralwertkurven, die die Fähigkeit des Auges beschreiben, einem Farbreiz ϕ eine Farbvalenz F zuzuordnen, lassen sich so für den Farbreiz ϕ die Farbwerte der Farbvalenz F im zugehörigen Primärvalenzsystem berechnen. Das System R, G, B bezieht sich auf die spektralen Primärvalenzen

mit einer relativen spektralen Strahlungsleistung S₇₀₀=72,096,

mit S_546,1=1,379 und

mit S_435,8=1,000. Neben diesem System ist 1931 von der Internationalen Beleuchtungskommission CIE das NormvalenzsystemX, Y, Z verabredet worden, in dem eine Farbvalenz durch die Farbgleichung F=XX+YY+ZZ mit den Normfarbwerten X, Y, Z gekennzeichnet ist. Die zunächst individuellen Zuordnungsergebnisse von Farbvalenzen zu Farbreizen sind für die Farbnormalsichtigen zum System des durchschnittlichen Beobachters (farbmetrischer Normalbeobachter) zusammengefaßt.

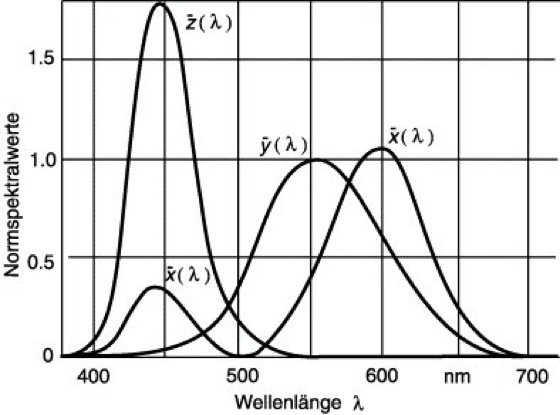
Die Transformation des Systems R, G, B in das System X, Y, Z ist so gewählt, daß die Normvalenzen X und Z keinen Beiwert zur Leuchtdichte der zu kennzeichnenden Farbvalenz liefern, der Normfarbwert Y ist also proportional zur Leuchtdichte. Die Einheiten der drei Normvalenzen sind so festgelegt, daß für den Farbreiz des energiegleichen SpektrumsX=Y=Z gilt. Die Normvalenzen sind virtuelle Farbvalenzen, d.h., sie sind nur zahlenmäßig konstruierbar und liegen außerhalb des Bereichs der reellen Farbvalenzen. Mit Hilfe der Normspektralwertkurven

(Abb.), die tabelliert vorliegen, werden die Normfarbwerte aus der relativen spektralen Energieverteilung berechnet. Es gilt

und das Analoge für Y und Z. Der Maßstabsfaktor k bleibt bei Selbstleuchtern unbestimmt, denn die Helligkeit wird zusätzlich durch eine photometrische Größe gekennzeichnet. Bei Körperfarben wird k so festgelegt, daß für die vollkommen mattweiße Fläche Y den Wert 100 annimmt.

Durch die Vereinbarung des Normalbeobachters nimmt die Farbvalenz die Natur einer mathematischen Funktion des Farbreizes an. Die Spektralwertkurven haben jedoch nur dann einen Sinn, wenn sie zu Ergebnissen führen, die mit der visuellen Wahrnehmung übereinstimmen.

Zusätzlich zum Normalvalenzsystem von 1931, das sich auf ein 2° großes Gesichtsfeld bezieht, wurde, da Farben meist bei einem größeren Gesichtsfeld beobachtet werden, 1964 das 10°- oder Großfeld-Normvalenzsystem mit den Primärvalenzen X₁₀, Y₁₀, Z₁₀ eingeführt; zwischen beiden Systemen gibt es keine Umrechnungsmöglichkeiten, da die physiologischen Grundlagen verschieden sind.

Für die Maßbestimmung von Filter- und Körperfarben sind neben den Festlegungen über das Maßzahlsystem (Wahl der Primärvalenzen) und den Normalbeobachter (2° oder 10°) noch zwei weitere notwendig, nämlich die Wahl der Normlichtart, mit der die Beleuchtung erfolgen soll, und der Meßgeometrie (Farbmessung). Für alle Festlegungen gibt es mehrere Möglichkeiten entsprechend den im Anwendungsfalle gegebenen Bedingungen.

2) Weil in dem auf der Grundlage der Mischungsbeziehungen mit Hilfe des Gleichheitsurteils aufgebauten Farbenraum wegen seiner affinen Struktur Farbabstände, d.h. empfundene Unterschiede zwischen Farbvalenzen, nicht durch geometrische Abstände abgebildet werden, ist in der höheren F. versucht worden, dem Farbenraum eine geeignete Metrik zuzuweisen. Durch die Einbeziehung von Urteilen über größere Ähnlichkeit und Ebenunterscheidbarkeit von Farbempfindungen soll es möglich werden, Aussagen über Farbempfindungsunterschiede zu machen und so zu einer zahlenmäßigen Bewertung von Farbabständen zu gelangen. Für gerade unterscheidbare Farben mit den Koordinatendifferenzen dx_i wird vermöge der Beziehung

ein Linienelement ds definiert, das den differentiellen Abstand der Farben im dreidimensionalem Raum angibt.

Damit kann eine Riemannsche Geometrie im Farbenraum aufgebaut werden; der Farbunterschied wird durch das über eine geodätische Linie erstreckte Integral ∫ds gemessen. Die Schwierigkeit besteht darin, die Koeffizienten g_ik so zu wählen, daß die Theorie mit der wirklichen Unterschiedsempfindlichkeit übereinstimmt. Bei den Versuchen zur Bestimmung der g_ik gibt es zwei verschiedene Wege. Der erste basiert auf theoretischen Überlegungen zur Funktionsweise des Sehmechanismus in Verbindung mit experimentellen Schwellenwerten (induktive Methode); auf diese Weise wurden Linienelemente unter anderem von H. Helmholtz, E. Schrödinger und W. S. Stiles abgeleitet. Bei der empirischen Methode werden die g_ik durch Analyse umfangreicher Gruppen von Meßwerten der Unterschiedsschwelle gewonnen (unter anderem D. L. MacAdam).

Die Definition eines Linienelementes scheint jedoch auf prinzipielle Schwierigkeiten zu stoßen, die sich aus folgenden experimentellen Tatbeständen ergeben: Die Unterschiedsschwellen um einen Farbpunkt sind möglicherweise nicht symmetrisch verteilt, und bei größeren Farbabständen entspricht in verschiedenen Bezirken des Farbenraumes einer gleichen Anzahl von Differentialelementen keine gleiche Unterschiedsempfindung. Das würde bedeuten, daß eine Metrik nicht-Riemannschen Charakter haben müßte. Die Annahme einer nichtlinearen Verarbeitung der Farbreize durch das visuelle System würde bedeuten, daß die Farbempfindungen keinen Raum, sondern ein Vektorfeld im affinen Farbenraum bilden.

Da praktische Bedürfnisse aber die zahlenmäßige Angabe von Farbdifferenzen und Toleranzen sowie Meßunsicherheiten erfordern, wurden durch empirische Transformation der Normfarbwerte an diesen Bedürfnissen orientierte mehr oder weniger empfindungsgemäß gleichabständige Farbsysteme geschaffen, die dies gestatten.

Farbmetrik: Normspektralwertkurven.