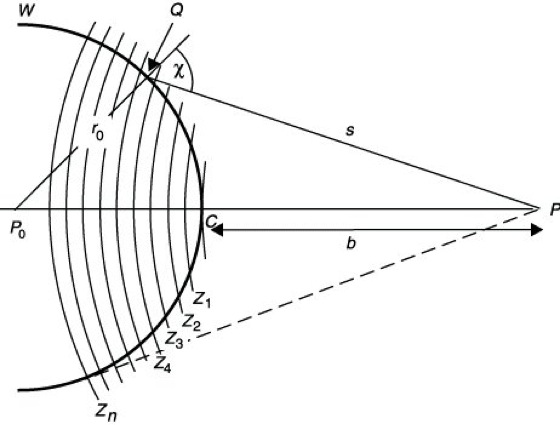
Fresnelsche Zonenkonstruktion (A. J. Fresnel, 1788-1827). In der Abb. sei P₀ ein Quellpunkt einer Kugelwelle Aexp(ikr)/r (mit k als Wellenzahl), und im Aufpunkte P interessieren Amplitude und Intensität des Lichtes. Eventuelle Blenden seien rotationssymmetrisch um die Achse P₀P angeordnet. Die Wellenfront W der von P₀ ausgehenden Kugelwelle wird von Fresnel unterteilt durch Kugelflächen, die in P zentriert sind und deren Radien von b an um jeweils λ/2 erhöht werden (λ Wellenlänge). Die auf W dadurch herausgeschnittenen Kreisringzonen werden Fresnelsche Zonen Z_i genannt. Beispielsweise reicht die Zone Z₁ von C bis zur zweiten gezeichneten Kugelfläche, die zweite Zone Z₂ von der zweiten zur dritten Kugelfläche usw. Für die Aufsummation der Lichterregung in P ist diese Zoneneinteilung zweckmäßig gewählt. Die von einem Flächenelemente df der Fläche W ausgehende Elementarwelle trägt nach dem Huygensschen Prinzip zur Lichterregung in P mit dem Anteil


(1)

bei. Dabei ist die Bedeutung von r₀, s und χ der Abb. zu entnehmen. Die Richtungsfunktion K(χ) hängt vom Winkel χ ab, und zwar fällt sie nach Fresnel von ihrem Maximalwerte bei χ=0 auf den Wert Null für χ=π/2 steil ab. (Eine eindeutige Festlegung erfolgt erst in der Kirchhoffschen Beugungstheorie.) Mit (1) läßt sich der Beitrag jeder Zone Z_i zur Gesamterregung in P ermitteln.

Für die Ausbreitung des Lichtes von P₀ nach P ohne eine Blende ergibt sich nach "angepaßter" Festlegung des Faktors K für Z₁, daß die Summation der Beiträge der einzelnen Fresnelschen Zonen (mit innerhalb einer Zone als konstant angenommenem Wert K) die von P₀ ausgehende ungestörte Kugelwelle in P reproduziert. Physikalisch ist die Reproduktion daher das Ergebnis der Interferenz aller von W ausgehenden Elementarwellen. Das ist die Bestätigung des Huygensschen Prinzips. Interessant ist die Wirkung der Abblendung von Zonen: Blendet man alle Zonen bis auf die erste halbe Zone ab, so erhält man in P die Lichterregung, wie sie auch bei ungehinderter Ausbreitung auftreten würde. Läßt man die ganze erste Zone offen, so erhält man in P die vierfache Intensität. Mit einer Kreisblende, die Z₁ und Z₂ offen läßt, resultiert in P völlige Dunkelheit, weil die von den beiden Zonen ausgehenden Wellen miteinander destruktiv interferieren (Gangunterschied λ/2). Mit weiterem Öffnen der Blende setzen sich die Intensitätsschwankungen fort, werden aber nach und nach undeutlicher. Das wird auch experimentell bestätigt.

Deckt man nur Z₁ ab, so ergibt sich in P dieselbe vierfache Intensität der ungestörten Lichtausbreitung, wie sie aus einem Abdecken aller anderen Zonen mit Ausnahme von Z₁ resultiert.

Eine weitere Intensitätserhöhung in P ist möglich, wenn die Zonen Z₂, Z₄ usw. abgedeckt werden, weil die von ihnen ausgehenden Wellen mit den von Z₁, Z₃ usw. ausgehenden nur destruktiv interferieren würden. Noch höher wird die Intensität, wenn Z₂, Z₄ usw. transparent bleiben, aber mit einer dielektrischen Schicht belegt werden, die die Phase des Lichtes um π verschiebt. Dann ist ihr Beitrag zu der genannten Interferenz konstruktiver statt destruktiver Art. Die Intensitätserhöhung in P ist ähnlich der Fokussierung von Strahlung durch eine Linse.

Die Lichtquelle P₀ in der Abb. kann auch bei -∞ liegen. Dann wird die einfallende Wellenfront eben, und man erhält mit den beschriebenen Zonenabdeckungen die Fresnelschen Zonenplatten.

Fresnelsche Zonenkonstruktion: P₀ Quellpunkt, P Aufpunkt; Z₁, Z₂, ... Fresnelsche Zonen, W Wellenfläche.