Gradientenoptik, eine optische Teildisziplin, die sich mit der Entwicklung von optischen Elementen mit räumlich kontinuierlich veränderlichem Brechungsindex befaßt. Letzterer weist dann einen Gradienten auf, was den Namen G. erklärt. Linsen mit einem ortsabhängigen Brechungsindex werden Gradientenlinsen genannt. Während der G. bislang nur akademische Bedeutung zukam, ist nunmehr – dank inzwischen entwickelter Techniken zur Erzeugung von Brechungsindexprofilen in verschiedenen Materialien – mit ihrem Einsatz für Zwecke der optischen Abbildung zu rechnen. Auf dem Gebiete der optischen Nachrichtenübertragung hat die G. bereits zur Fertigung von Gradientenfasern geführt.

Grundsätzlich sind drei Typen des Brechungsindexverlaufs von Bedeutung.

1) Axialer Gradient. Der Brechungsindex variiert in Richtung der optischen Achse. Es konnte (zunächst rechnerisch) gezeigt werden, daß eine asphärische Linse einer sphärischen Linse mit einem geeigneten axialen Gradienten gleichwertig ist. Die Abb. macht an einem durchgerechneten Beispiel deutlich, wie die große sphärische Aberration einer Einzellinse aus homogenem Material durch Herstellung eines axialen Gradienten geeigneter Größe beseitigt werden kann.

2) Radialer oder zylindrischer Gradient. Der Brechungsindex ändert sich (rotationssymmetrisch) in radialer Richtung bezüglich der optischen Achse. Ein solches Profil liegt bei der Gradientenfaser (optische Nachrichtenübertragung) und der von zwei parallelen ebenen Flächen begrenzten stabförmigen Woodschen Linse vor. Letztere wurde 1905 von R. W. Wood aus einem Glycerinstab hergestellt. Durch zeitweiliges Eintauchen in Wasser erreichte er, daß der Stab Wasser in einer mit dem Abstand von der Achse variierenden Konzentration enthielt.

Für Abbildungszwecke ist eine parabolische Brechzahlverteilung

am günstigsten. Dabei bezeichnen ρ den Abstand von der Achse des Zylinders, a dessen Radius und n₀ den Brechungsindex in der Zylindermitte. Weiterhin gilt Δn=n₀-n_a mit n_a als Brechungsindex auf der Zylinderoberfläche. Führt man die Konstante

ein, so läßt sich die Brechzahlverteilung schreiben als

In einem Lichtleiter mit einem solchen Brechungsindexprofil (Gradientenfaser) beschreibt die Bahn eines Lichtstrahles eine wellenförmige (sinusförmige) Kurve mit der Periode 2π/b. Eine zylinderförmige, von zwei ebenen Flächen begrenzte Gradientenlinse der Dicke d mit der obigen Brechzahlverteilung hat fokussierende Eigenschaften. Die bildseitige Brennweite beträgt


.

3) Sphärischer Gradient. Der Brechungsindex ändert sich kugelsymmetrisch mit dem Abstand von einem Zentrum. Eine solche Brechzahlverteilung zeigen das (nur theoretisch interessante) Maxwellsche Fischauge und die – bis jetzt hauptsächlich zur Fokussierung eines parallelen Bündels von Mikrowellen benutzte – Kugellinse nach Luneburg, bei der sich der Brechungsindex n gemäß der Beziehung

mit dem Abstand r vom Mittelpunkt (0≤r≤a mit a als Radius der Linse) ändert. Neuerdings wird die Luneburg-Linse für die Zwecke der integrierten Optik in Dünnschichttechnik hergestellt.

Herstellungsverfahren. Die Fertigung von Gradientenfasern erfolgt so, daß Glasmaterial in Schichten unterschiedlicher chemischer Zusammensetzung (die sich demzufolge auch in ihrem Brechungsindex unterscheiden) aus der Gasphase entweder auf der Außen- oder der Innenseite eines Rohres chemisch abgeschieden wird (chemical vapor deposition, abgekürzt CVD). Durch anschließendes Ziehen des Glases zu einer Faser erreicht die Dicke der Schichten Werte, die kleiner als die Wellenlänge sind, so daß dabei der ursprünglich sprunghafte Verlauf des Brechungsindexes in einen stetigen umgewandelt wird. Eine stabile, reproduzierbare Verteilung des Brechungsindexes ist jedoch nur mit hohem technologischen Aufwand erreichbar. Das am häufigsten verwendete Verfahren zur Herstellung optischer Elemente wie Linsen ist der Ionenaustausch in Salzschmelzen. Dabei diffundieren z.B. Lithiumionen aus einer Lithiumbromidlösung in das Glas und nehmen die Stelle von Natrium ein.

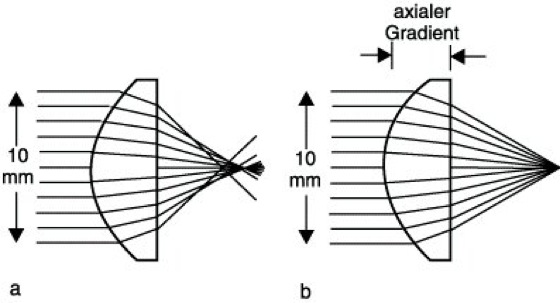
Gradientenoptik: Abbildung mittels einer Linse aus homogenem Material (a) und einer Gradientenlinse (b). Das Öffnungsverhältnis beträgt 0,85.