Hologramminterferometrie, holographische Interferometrie, Interferometrie unter Benutzung von Wellenfronten, die in Hologrammen gespeichert sind. Da jede holographische Aufnahmeanordnung (Abb. 1) ein Interferometer darstellt, ist sie prinzipiell auch zur H. nutzbar. Wesentlicher Bestandteil eines Hologramminterferometers ist das Hologramm. In diesem wird z.B. der Ausgangszustand eines Objektes (d.h. seine streuende Oberfläche) zu Beginn eines Experimentes aufgezeichnet. Nach Repositionieren des entwickelten Hologramms läßt sich durch Überlagerung der Objektwelle, welche die Information über den aktuellen Zustand des Objektes enthält, mit der von der Rekonstruktionswelle aufs neue erzeugten Objektwelle ein Interferenzbild erzeugen. Interferenzstreifen lassen sich immer dann beobachten, wenn sich die beiden Wellenfelder makroskopisch und vor allem mikroskopisch nur geringfügig unterscheiden. Die hauptsächliche Anwendung ist daher der Nachweis von Zustandsänderungen von Objekten, die zu geringen geometrischen Deformationen führen.

1) Aufnahmetechniken. Es lassen sich hauptsächlich drei Verfahren unterscheiden: die Doppelbelichtungs-, die Echtzeit- und die Zeitmittelungstechnik.

Bei der Doppelbelichtungstechnik werden die beiden Objektzustände in ein und demselben Hologramme aufgezeichnet. Bei der Rekonstruktion des Hologramms werden die beiden Objektwellen gleichzeitig wieder erzeugt und interferieren daher miteinander. Dabei ergibt sich eine Intensitätsverteilung der Form I∝cos²(Φ/2), wobei Φ=Φ₁-Φ₂ die Differenz der (ortsabhängigen) Phasen Φ₁ und Φ₂ der beiden Objektwellen bedeutet (Abb. 2).

Ein wichtiger Sonderfall ist die Doppelbelichtungstechnik mit zwei getrennten Referenzwellen (je eine pro Objektzustand). Dadurch ergeben sich günstige Auswertungsmöglichkeiten, z.B. für Heterodyninterferometer.

Bei der Echtzeittechnik wird zunächst die Information über den Ausgangszustand holographisch gespeichert. Nach Entwicklung und Repositionierung des Hologramms erfolgt ein interferometrischer Vergleich der rekonstruierten mit der aktuellen Objektwelle. Da die Rekonstruktion im allgemeinen nur schwache Wellenfelder liefert, ist eine Intensitätsregelung nötig, um guten Kontrast zu erhalten. Gegenüber der Doppelbelichtungstechnik ergibt sich eine Phasenverschiebung um 180°, da das Hologramm ein photographisches Negativ darstellt.

Zur Zeitmittelungstechnik greift man insbesondere bei Schwingungsuntersuchungen von Objekten. Dabei erfolgt eine holographische Aufnahme des bewegten Objektes während einer Zeit T, die groß im Vergleich zur Schwingungsdauer ist. Es werden so die unterschiedlichen Lagen der Objektflächen in Gestalt einer Vielzahl von Einzelhologrammen aufgezeichnet. Bei der Rekonstruktion des Hologramms entsteht dann ein Wellenfeld, das eine Superposition der den verschiedenen Positionen der Objektfläche entsprechenden Objektwellen darstellt. Wenn sich die Oberfläche am Orte mit den Koordinaten x,y um die Strecke D(x, y)cos(Ωt) in Richtung der Oberflächennormalen verschiebt, ändert sich die Phase des gestreuten Lichtes um den Wert Φ(t)=2πD(x,y)cos(Ωt) (sinΘ₁+sinΘ₂)/λ, wobei λ die Wellenlänge und Θ₁, Θ₂ die Winkel bezeichnen, welche die Beleuchtungs- und die Beobachtungsrichtung mit der Oberflächennormalen einschließen. Die komplexe Amplitude des rekonstruierten Wellenfeldes ist dann proportional zu dem Integral

, und die Intensitätsverteilung ergibt sich als proportional zu

, wobei J₀ die Bessel-Funktion nullter Ordnung bedeutet. Das Bild des schwingenden Objektes ist daher mit Interferenzkurven überzogen (Abb. 3). Die dunklen Kurven entsprechen dabei Nullstellen der Bessel-Funktion. Mittels stroboskopischer Verfahren läßt sich der starke Kontrastabfall im Falle größerer mechanischer Schwingungsamplituden beheben.

2) Auswertung. Die quantitative Auswertung von Hologramminterferogrammen kann mit Echtzeitinterferometern erfolgen. Unterscheiden sich die beiden gespeicherten Objektzustände dadurch, daß eine Verformung des Körpers eingetreten ist, so ist der Zusammenhang zwischen der oben erwähnten Phasendifferenz Φ, deren Wert der Intensitätsverteilung im Interferogramm entnommen werden kann, und der an der betreffenden Stelle der Objektoberfläche stattgefundenen Verschiebung s eines Oberflächenelementes bei einer Auflichtmessung gegeben durch Φ=(k₁+k₂)s, wobei k₁, k₂ die Wellenzahlvektoren für die Beleuchtungs- und die Beobachtungsrichtung bedeuten. Die Komponenten von s lassen sich durch Beobachtung und/oder Beleuchtung in verschiedenen (mindestens drei) Richtungen erschließen.

Bei Durchlichtobjekten, wie sie z.B. in der Plasmadiagnostik vorliegen, unterscheiden sich die beiden Objektzustände in der räumlichen Brechzahlverteilung. (Das Objekt kann auch mit Luft verglichen werden; in einem Hologramm werden dann zunächst die Fehler des leeren (luftgefüllten) zur holographischen Aufnahme benutzten Interferometers aufgezeichnet.) Sei die Brechzahlverteilung in dem einen Falle konstant (n₀), in dem anderen Falle räumlich veränderlich (n(x,y,z)), so ist die Phasendifferenz Φ gegeben durch Φ=2πG/λ, wobei G den Gangunterschied G(x,y) = ∫[n(x,y,z)-n₀]dz längs der Durchstrahlungsrichtung z bezeichnet. Die gesuchte Größe n(x,y,z) muß durch mathematische Inversion berechnet werden. Spezialfälle allgemeiner Brechzahlverteilungen n(x,y,z) sind zweidimensionale n=n(x,y) und rotationssymmetrische n=n(ρ,y) (Rotationsachse ist die y-Achse, ρ²=x²+z²). Die Auflösung nach n ist im ersten Falle trivial. Im zweiten Falle führt die Inversion auf eine Abelsche Integralgleichung, die näherungsweise auf ein lineares Gleichungssystem zurückgeführt werden kann. Im folgenden sei ein Schnitt senkrecht zur Symmetrieachse der n-Verteilung betrachtet. Abb. 4 illustriert die Summation der optischen Wege zum Gangunterschied G(x):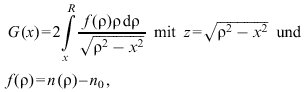

wobei R den Radius des Zylinders bedeutet. Zur genäherten numerischen Auswertung wird der Zylinder in I Hohlzylinder der Dicke Δρ zerlegt und f(ρ) im Bereich ρ_k≤ρ≤ρ_k+1 (k=0,1,2,..., I-1) als konstant angenommen und mit f_k bezeichnet. Damit schreibt sich der Gangunterschied für einen Lichtstrahl, der die Probe in einem Abstande ρ_i=iΔρ passiert, als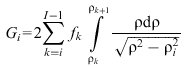

Durch Aufschreiben der vorstehenden Gleichung für die verschiedenen Werte von i, von i=I-1 beginnend, erhält man ein lineares Gleichungssystem, dessen rechte Seite ein dreieckiges Schema bildet und das daher leicht nach den f_k aufgelöst werden kann. Im Falle fehlender Symmetrie ist die Inversion nur durch multidirektionale Auswertung, welche entsprechende Objektbeleuchtung voraussetzt, möglich. Diese Verfahren sind verwandt mit den Methoden, die in der Röntgentomographie angewandt werden.

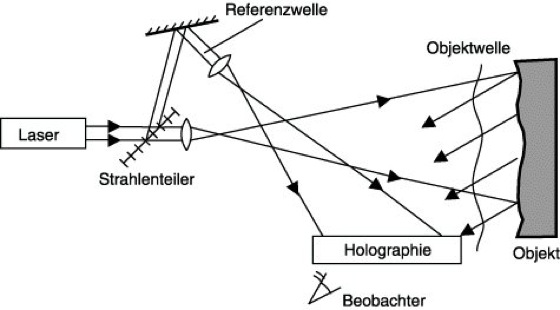
Hologramminterferometrie 1: Holographische Aufnahmeanordnung, die sich auch zur Hologramminterferometrie nutzen läßt.

Hologramminterferometrie 2: Doppelbelichtungsaufnahme eines Kugellagers. Sie zeigt mechanische Verformungen unter dem Einfluß des Spannfutters einer Drehbank.

Hologramminterferometrie 3: Zeitlich gemittelte Aufnahme (Interferenzbild) einer mit 2,5 kHz schwingenden Telefonmembran.

Hologramminterferometrie 4: Zur Berechnung des Gangunterschiedes für ein rotationssymmetrisches Phasenobjekt.