Interferenzen in Kristallen, bei Durchgang linear polarisierten Lichtes durch doppelbrechende Kristalle unter Verwendung eines Analysators zu beobachtende Interferenzerscheinungen. Für die Beschreibung der I. i. K. sind entsprechend der Kristalloptik die Wellengeschwindigkeiten und die Brechungsindizes wesentlich, während die Strahlgeschwindigkeiten hierbei weniger wichtig sind, da die Bündelbegrenzungen meist keine Rolle spielen. Trifft mit Hilfe eines Polarisators erzeugtes Licht auf einen doppelbrechenden Kristall, so wird je nach Orientierung der Ausbreitungsrichtung des Lichtes im Kristalle die Strahlung in zwei senkrecht zueinander schwingende Komponenten zerlegt, die sich im Kristalle mit unterschiedlichen Wellennormalengeschwindigkeiten entsprechend unterschiedlichen Brechungsindizes n₁ und n₂ ausbreiten. Dadurch entsteht ein Gangunterschied zwischen beiden Komponenten der Größe Δs=(n₁-n₂)d, wobei d die Kristalldicke in Durchstrahlungsrichtung bedeutet, genauer das Mittel der von den beiden Komponenten durchlaufenen Wege. Durch Multiplikation von Δs mit der Wellenzahl erhält man die zugehörige Phasendifferenz. Die beiden senkrecht zueinander polarisierten Komponenten können nicht miteinander interferieren. Eine Interferenz ist jedoch dann zu beobachten, wenn man das Licht durch einen zweiten Polar, den Analysator, hindurchtreten läßt. Dabei wird von jeder Teilwelle nur der Anteil durchgelassen, der in der durch die Analysatorstellung festgelegten Richtung schwingt, und diese Anteile interferieren miteinander. Je nach Gangunterschied und Stellung des Analysators erfolgt dabei eine mehr oder weniger vollständige Auslöschung oder Verstärkung. Es ist zweckmäßig, den Gangunterschied Δs in Einheiten der Vakuumwellenlänge λ₀ auszudrücken: Δs=mλ₀. Der ganzzahlige Anteil von m gibt die Ordnung der Interferenz an. Ist m eine ganze Zahl, so haben die beiden Wellen an der Austrittsfläche die gleiche Schwingungsphase. Sie superponieren sich daher wieder zu der ursprünglichen linear polarisierten Welle. Steht die Schwingungsrichtung des Analysators senkrecht auf der Schwingungsrichtung des Polarisators (gekreuzte Polare), so tritt daher kein Licht aus; es erfolgt Auslöschung unabhängig von der Orientierung des Kristalles. Ist m dagegen ein ungeradzahliges Vielfaches von 1/2, so erhält man bei gekreuzten Polaren maximale Helligkeit, die aber noch von der Orientierung des Kristalles abhängt (Polarisationsmikroskopie). Am günstigsten ist die Diagonalstellung (s.u.). Bei monochromatischer Einstrahlung erscheinen die Interferenzen hell-dunkel, bei Einstrahlung von weißem Licht in verschiedenen Farben (Interferenzfarben, Polarisationsfarben, chromatische Polarisation). Bei kleinem Gangunterschied sind diese Farben intensiv, da nur ein oder zwei Wellenlängenbereiche durch destruktive Interferenz ausgelöscht werden. Die anschließenden (niedrigen) Ordnungen zeigen ähnliche Farbfolgen. Man spricht daher z.B. von Rot 1. Ordnung, Rot 2. Ordnung usf. Mit zunehmendem Gangunterschiede werden die Farben jedoch immer blasser, da hier für immer mehr Wellenlängen die Bedingung für destruktive Interferenz erfüllt wird, und das übrigbleibende Licht wird vom Auge als weiß empfunden. Zur Beobachtung der I. i. K. wird vorwiegend das Polarisationsmikroskop (die dortige Abb. 2) verwendet. Dabei werden orthoskopischer und konoskopischer Strahlengang unterschieden:

1) Beim orthoskopischen Strahlengang (Abb. 1) wird das Polarisationsmikroskop auf die Beobachtung der Objektebene eingestellt, um für jeden Punkt O des Kristalles KR Information über den Durchgang polarisierten Lichtes zu erhalten. Je nachdem, ob bei Drehung des zwischen gekreuzten Polaren befindlichen Kristalles ein Wechsel von Dunkelheit und Aufhellung erfolgt oder keine Aufhellung stattfindet, ist der Kristall in der Beobachtungsrichtung doppelbrechend oder isotrop. Bei doppelbrechenden Kristallen kann an Hand der beobachteten Interferenzfarben der Gangunterschied geschätzt oder unter Verwendung von Kompensatoren, die definierte (teilweise kontinuierlich veränderliche) zusätzliche Gangunterschiede zwischen den beiden Lichtkomponenten erzeugen, gemessen werden. Aus dem Gangunterschied ergeben sich bei bekannter Kristalldicke der Unterschied der Brechungsindizes und damit Hinweise auf die Art der Kristalle.

Bei Drehung des Kristallpräparates zwischen gekreuzten Polarisatoren erfolgt stets in den Stellungen eine Auslöschung des Lichtes (Dunkelheit), in denen die Schwingungsrichtungen im Kristall mit den Schwingungsrichtungen der Polare übereinstimmen (Normalstellung).

Durch den Kristall breitet sich in diesem Falle linear polarisiertes Licht aus. Dreht man den Kristall um 45° zur Normalstellung, so hat man in Diagonalstellung maximale Aufhellung. Durch solche Untersuchungen lassen sich Aussagen über die kristallographische Orientierung des Kristallschnittes gewinnen. Im orthoskopischen Strahlengange sind die beiden Fälle "Analysator senkrecht zum Polarisator" und "Analysator parallel zum Polarisator" möglich. Dort, wo in einem Falle Helligkeit zu beobachten ist, liegt im anderen Falle Dunkelheit vor und umgekehrt. Zu einer Färbung in dem einen Falle gehört die Komplementärfärbung in dem anderen Falle. Beispiele für Bilder im orthoskopischen Strahlengang zeigt Abb. 2.

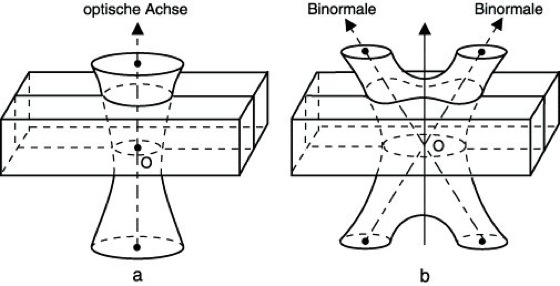
2) Für den konoskopischen Strahlengang (Abb. 1) wird das Polarisationsmikroskop auf die Beobachtung der hinteren Objektivbrennebene HB eingestellt. Damit ist an jedem Punkte K in der besagten Brennebene das Interferenzverhalten des diesem Punkte zugeordneten parallelen Strahlenbündels beim Durchgange durch den Kristall KR abzulesen. Die bei konoskopischem Strahlengange zu beobachtenden Interferenzerscheinungen werden als Achsenbilder bezeichnet. Die möglichen Achsenbilder kann man sich an der Bertinschen Fläche (Fläche gleichen Gangunterschiedes, A. Bertin 1861) veranschaulichen (Abb. 3). Sie entsteht, wenn man von einem Punkte O aus nach jeder Richtung diejenige Strecke abträgt, die das Licht in dieser Richtung im Kristalle durchlaufen muß, damit der Gangunterschied einen gegebenen Wert annimmt. Bei gekreuzten Polaren tritt bei Δs = mλ₀ (m ganz) destruktive und bei Δs=(m+1/2)λ₀ konstruktive Interferenz auf. Die Schnittkurven der Bertinschen Fläche für ganzzahliges m mit der Kristalloberseite sind die zu beobachtenden Interferenzkurven.

Neben diesen Interferenzkurven werden noch die sogenannten Hauptisogyren beobachtet. Diese treten (bei gekreuzten Polaren) als dunkle Interferenzkurven dann auf, wenn die (durch den Polarisator festgelegte) Polarisationsrichtung des einfallenden Lichtes mit einer der beiden Schwingungsrichtungen im Kristall zusammenfällt. Den beiden (zueinander senkrechten) Schwingungsrichtungen im Kristalle entsprechen die beiden Hauptisogyren. Allgemein sind Isogyren definiert als Kurven gleicher Polarisationsrichtung des Lichtes in der hinteren Brennebene (Abb. 1).

Spezielle Fälle. An einer senkrecht zur Achse eines einachsigen Kristalles geschnittenen Kristallplatte beobachtet man bei monochromatischer Beleuchtung zwischen gekreuzten Polaren ein dunkles Kreuz in den Auslöschungsrichtungen und ein System von Interferenzringen (Abb. 2, Bild IIa und IIb). Die Interferenzringe stellen Kurven mit gleichem Gangunterschiede dar, wobei jedem Ringe ein anderer Neigungswinkel der Strahlen KS gegenüber dem Kristall KR in Abb. 1 entspricht. Das dunkle Kreuz repräsentiert die Hauptisogyren. Ein zusätzliches Lambda-Viertel-Plättchen führt zur Aufhellung der Hauptisogyren. Bei Weißlichtbeleuchtung ergeben sich Interferenzringsysteme unterschiedlicher Farbe, die als Isochromaten bezeichnet werden. Bei Änderung der Lage der Kristallachsen ändert sich die Form der Hauptisogyren und der Isochromaten. Bei zweiachsigen Kristallen, die senkrecht zur spitzen Bisektrix geschnitten sind, zeigen die Hauptisogyren einen hyperbelförmigen Verlauf, und die Isochromaten bilden charakteristische Kurven (darunter auch die Lemniskate, die die Form eines ∞-Zeichens hat), wenn man die Kristallplatte zwischen gekreuzten Polarisatoren in die Diagonalstellung dreht (Abb. 2, Bild IIIa und IIIb). Die durch Einschaltung von Lambda-Viertel-Plättchen hervorgerufene Verschiebung der Isochromaten gibt Auskunft über den optischen Charakter (optisch positiv oder negativ) des untersuchten Kristalles.

Bei optisch aktiven Kristallen (optische Aktivität) verursacht die Drehung der Polarisationsebene eine Änderung der Achsenbilder, die in der Regel jedoch nur bei großer Aktivität oder größerer Kristalldicke zu beobachten ist. Z.B. sind bei einer senkrecht zur Achse geschnittenen Quarzplatte die Hauptisogyren in der Mitte des Achsenbildes unterbrochen (Abb. 2, Bild IV). In der Mitte tritt eine Aufhellung auf. Bringt man eine links- und eine rechtsdrehende Quarzplatte übereinander in den konoskopischen Strahlengang mit gekreuzten Polaren, so haben die Hauptisogyren eine spiralförmige Gestalt (Airysche Spiralen, Abb. 2, Bild Va und Vb). Diese Spiralen sind rechts- oder linksgewunden je nachdem, ob das Licht zuerst den Rechts- oder den Linksquarz durchsetzt. Sie werden unregelmäßig, wenn die Quarzplatten nicht genau senkrecht zur optischen Achse geschnitten sind (Prüfmittel). Zweiarmige Airysche Spiralen treten bei Kombination eines Lambda-Viertel-Plättchens mit Quarz auf (Abb. 2, Bild Vc). Eine Druckspannung im Quarz ist im konoskopischen Strahlengange nachweisbar (Abb. 2, Bild VIa und VIb). Plattenstapel zweiachsiger Kristalle zeigen komplizierte Interferenzerscheinungen (Abb. 2, Bild VIIa und b). Die Interferenzen in zweiachsigen Kristallen werden infolge einer Dispersion der optischen Achsen wellenlängenabhängig.

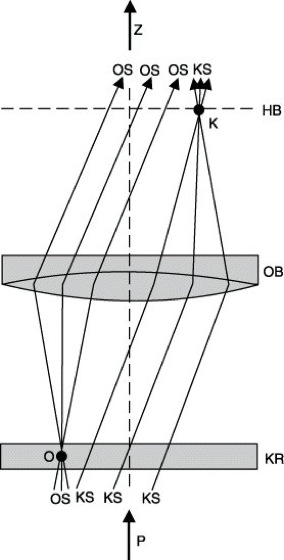
Interferenzen in Kristallen 1: Orthoskopischer (OS) und konoskopischer (KS) Strahlengang im Polarisationsmikroskop. P Licht, aus der Anordnung von Lichtquelle, Polarisator und Kondensor kommend; KR Kristall, OB Objektiv, HB hintere Brennebene des Objektivs; Z zu Analysator, Amici-Bertrandscher Linse und Zwischenbild im Mikroskop.

Interferenzen in Kristallen 2:
Orthoskopischer Strahlengang (nach H. Freund (Hrsg.) Handbuch der Mikroskopie in der Technik, Band IV Mikroskopie der Silikate, Teil I Mikroskopie der Gesteine, Umschau Verlag, Frankfurt am Main, 1955, S. 357, S. 404):
Ia: Gleitzwillingslamellen (optisch einachsig) in Calcit (Marmor); gekreuzte Polare.
Ib: Pyroxeneinsprenglinge (optisch zweiachsig) in Terphrit; gekreuzte Polare.
Konoskopischer Strahlengang (nach H. Hauswaldt, "Interferenzerscheinungen an doppelbrechenden Kristallen im konvergenten polarisierten Licht", Bände I, III, Magdeburg 1902, 1907):
IIa: Zirkonplatte, senkrecht zur optischen Achse geschnitten, im Na-Licht zwischen gekreuzten Polaren.
IIb: Wie in IIa, mit zusätzlicher λ/4-Platte.
IIIa: Aragonitplatte, senkrecht zur ersten Mittellinie geschnitten, im Na-Licht zwischen gekreuzten Polaren, Normalstellung.
IIIb: Wie in IIIa, jedoch Diagonalstellung.
IV: Quarz (optisch aktiv), senkrecht zur optischen Achse geschnitten, zwischen gekreuzten Polaren.
Va: Vierfache rechtsgewundene Airysche Spirale an zwei Quarzplatten, senkrecht zur optischen Achse geschnitten; gekreuzte Polare. Zunächst wird ein Rechtsquarz vom Lichte durchlaufen, danach ein Linksquarz.
Vb: Vierfache linksgewundene Airysche Spirale; wie Va, jedoch wird der Linksquarz zuerst vom Lichte durchlaufen.
Vc: Rechte Airysche Doppelspirale; Rechtsquarz, kombiniert mit λ/4-Platte.
VIa, b: Druckbedingter Übergang von optisch einachsigem zu zweiachsigem Verhalten und damit Aufspaltung der Airyschen Spirale. Einseitig komprimierte linksdrehende Quarzplatte (Druckrichtung links-rechts), senkrecht zur optischen Achse geschnitten. Zirkular polarisiertes und zirkular analysiertes Licht bei unterschiedlicher Orientierung einer λ/4-Platte.
VIIa: Drei Paare von Titanitplatten hintereinander, jedes Paar bestehend aus zwei Titanitplatten, die zur ersten Mittellinie gekreuzt sind; Diagonalstellung, Polare gekreuzt.
VIIb: Wie in VIIa, jedoch Polare parallel.

Interferenzen in Kristallen 3: Bertinsche Fläche für einen optisch einachsigen (a) und einen zweiachsigen (b) Kristall.