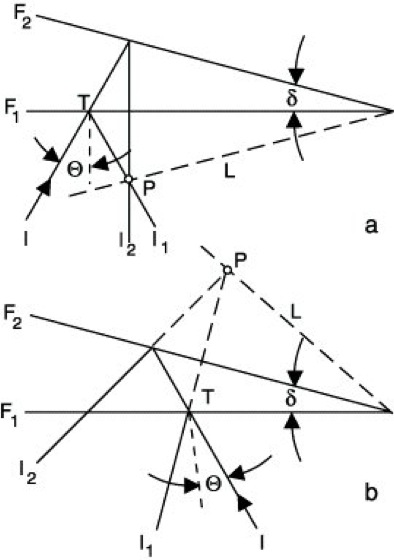
Interferenzkurven, 1) I. gleicher Dicke, Interferenzen gleicher Dicke, Fizeausche Streifen, Keilinterferenzen, entstehen an durchsichtigen Medien mit örtlich unterschiedlicher Dicke in Reflexion und Transmission. Sie folgen den Stellen gleicher optischer Dicke nd, wobei n den Brechungsindex des Mediums und d seine (örtliche) geometrische Dicke bezeichnen. Sie lassen sich am einfachsten an einem Keile beobachten. Dieser wird von zwei um einen kleinen Winkel δ (Keilwinkel) gegeneinander geneigten ebenen Fläche F₁ und F₂ (Keilflächen) gebildet. I. kommen dann in Reflexion folgendermaßen zustande (Abb.): Ein unter dem Einfallswinkel Θ auffallender Lichtstrahl l wird sowohl an der Fläche F₁ als auch nach deren Durchsetzen an der Fläche F₂ reflektiert; die beiden so entstehenden Hauptstrahlen l₁ und l₂ sind kohärent und kommen im Punkte P zur Interferenz. Je nachdem, ob der Schnittpunkt P, der Ort der Interferenzerscheinung, reell oder virtuell ist, unterscheidet man Interferenzen am a) reellen oder b) virtuellen Keile. Die optische Weglängendifferenz der Teilstrahlen vom Teilungspunkte T bis zum Vereinigungspunkte P, der Gangunterschied G, ergibt sich in Abhängigkeit von der örtlichen optischen Keildicke nd zu G=2nd cos(δ±Θ), wobei das obere Vorzeichen für reelle, das untere für virtuelle Punkte P gilt. G ändert sich mit d über die ganze Keilfläche. Ist Θ konstant, dann ist G nur von der Dicke d abhängig; je nachdem, ob G ein geradzahliges oder ungeradzahliges Vielfaches der halben Wellenlänge λ/2 ist, erreicht die Lichtintensität ihr Maximum oder es findet Auslöschung statt. Für senkrechten Lichteinfall Θ=0 und sehr kleine Keilwinkel δ ergibt sich die einfache Beziehung G=2nd, d.h., der Unterschied der Keildicke von einer zur nächsten Auslöschung (Streifenabstand) beträgt λ/2n. Sind die Keilflächen absolut eben, dann sind die I. gerade, parallele und äquidistante Streifen. Sie liegen (bei Einstrahlung von kollimiertem Licht) in einer Ebene (Lokalisationsebene), die durch die Keilkante geht (Abb.), und sind in der Nähe der Keilkante am kontrastreichsten. Nimmt man als eine der beiden Flächen (F₁) eine mit hinreichender Genauigkeit ebene, dann kann sie als Vergleichsfläche für eine zweite unregelmäßige (etwa technische) Oberfläche F₂ dienen, und die erhaltenen I. sind ein getreues Abbild der Oberflächenabweichungen von F₂.

An durchsichtig versilberten Keilplatten, deren Keilwinkel einige Minuten betragen, treten durch Zusammenwirken vieler Strahlen Interferenzstreifen mit steiler, nichtsinusförmiger Intensitätsverteilung auf (Vielstrahlinterferenzen). Zu den I. gleicher Dicke zählen auch die Newtonschen Ringe.

2) I. gleicher Neigung, Interferenzen gleicher Neigung, entstehen durch Interferenz des Lichtes einer quasimonochromatischen, normalerweise ausgedehnten Quelle an einer planparallelen Platte in Reflexion oder Transmission. Sie werden im Unendlichen beobachtet. Der Name rührt daher, daß zu einem bestimmten Intensitätswert der Interferenzerscheinung alle die Strahlen beitragen, die unter einem bestimmten Einfallswinkel auf die Plattenoberfläche treffen. Die wichtigsten I. gleicher Neigung sind die Haidingerschen Ringe. Bei verspiegelten Flächen hoher Reflexion treten auch hier Vielstrahlinterferenzen auf. Zu den I. gleicher Neigung zählen auch die Brewsterschen Streifen.

Interferenzkurven: Keilinterferenzen. a) reelle, b) virtuelle Interferenzen. F₁, F₂ Keilflächen, L Lokalisationsebene der Interferenzen, Θ Einfallswinkel, δ Keilwinkel, T Teilungspunkt, P Vereinigungspunkt.