Korrelationsfunktionen des Strahlungsfeldes, Funktionen, welche die Korrelationen beschreiben, die zwischen den Lichterregungen an verschiedenen Orten und/oder zu verschiedenen Zeiten bestehen. Amplitude und Phase der Lichtschwingung an einem festen Ort fluktuieren vor allem bei thermischem Licht sehr stark. Bei der Strahlung eines Einmodenlasers dagegen ist die Amplitude stabilisiert, doch es treten Phasenschwankungen auf. Die Schwankungen der Strahlungsfeldgrößen sind statistisch unabhängig, wenn die Beobachtungsorte r₁ und r₂ bei gleichzeitiger Beobachtung weit voneinander entfernt sind oder die Beobachtungszeiten t und t+τ (t variabel und τ fest) bei Beobachtung am gleichen Ort sich stark unterscheiden. Dies ist jedoch nicht so, wenn sich die beiden Orte (für τ=0) innerhalb eines Kohärenzvolumens (Kohärenz) befinden oder die zeitliche Verzögerung τ (für r₁=r₂) dem Betrage nach die Kohärenzzeit nicht überschreitet. Es bestehen dann Korrelationen zwischen den betreffenden Feldstärkewerten. Sie finden ihren mathematischen Ausdruck in der Korrelationsfunktion 1. Ordnung


. (1)

Dabei bezeichnen E^(-) und E⁽⁺⁾ den negativen bzw. positiven Frequenzanteil der elektrischen Feldstärke E. Es wurde vorausgesetzt, daß das Strahlungsfeld linear polarisiert ist. Andernfalls ist unter E eine kartesische Komponente der elektrischen Feldstärke zu verstehen. Die Größen E^(-) und E⁽⁺⁾ sind folgendermaßen definiert: Man denkt sich eine Fourier-Zerlegung von E in der Form


(2)

ausgeführt; dann ist


(3)

und


(4)

Da E eine reelle Größe ist, besteht die Beziehung E(r,-ν)=E*(r,ν), und es gilt


. (5)

Die Größe 2 E⁽⁺⁾(r,t) wird auch als das zu E(r,t) gehörige komplexe analytische Signal bezeichnet. Wir setzen voraus, daß es sich um ein stationäres Strahlungsfeld handelt. Die spitzen Klammern in (1) symbolisieren den Mittelwert bezüglich t über eine sehr lange Zeit. Aus historischen Gründen ist es in der Optik üblich, zur Beschreibung von Korrelationen an Stelle von G⁽¹⁾ die Funktion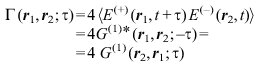


(6)

zu benutzen.

Sorgt man durch eine geeignete Interferenzanordnung dafür, daß sich die elektrischen Feldstärken E(r₁,t) und E(r₂,t+τ) an einem bestimmten Orte gleichzeitig überlagern (Kohärenz), so führen die durch (1) bzw. (6) beschriebenen Korrelationen zum Auftreten einer Interferenzerscheinung (Interferenz). Die Korrelationsfunktion G⁽¹⁾ bzw. Γ kann daher grundsätzlich aus Interferenzversuchen ermittelt werden (Interferenz). Dabei hat τ die Bedeutung des durch die Lichtgeschwindigkeit c dividierten Gangunterschieds der beiden interferierenden Wellen. Überdies kann die räumliche Korrelation G⁽¹⁾(r₁,r₂;0) bzw. Γ(r₁,r₂;0), wobei r₁ und r₂ in einer zur Ausbreitungsrichtung des Lichtes senkrechten Ebene liegen, im Falle thermischer Lichtquellen mit Hilfe des van Cittert-Zernike-Theorems berechnet werden. Der Betrag von G⁽¹⁾(r₁,r₂;τ) bzw. Γ(r₁,r₂;τ) nimmt seinen Maximalwert für r₁=r₂ und τ=0 an – in diesem Falle beschreibt die Korrelationsfunktion die Intensität am Orte r₁ – und fällt sowohl mit zunehmendem räumlichen Abstand |r₂-r₁| (für τ=0) als auch mit wachsender zeitlicher Verzögerung |τ| (für r₁=r₂) auf den Wert Null ab. Aus dem Abfall mit |r₂-r₁| in einer zur Ausbreitungsrichtung senkrechten Ebene bestimmt sich das Kohärenzintervall, aus dem Abklingen mit |τ| die Kohärenzzeit.

Von großem physikalischem Interesse ist auch die Fourier-Transformierte G⁽¹⁾(r₁,r₂;ν) von G⁽¹⁾(r₁,r₂;τ). Da G⁽¹⁾(r₁,r₂;τ), wie sich zeigen läßt, keinen negativen Frequenzanteil besitzt, gelten die Beziehungen


(7)


(8)

In der Optik schreibt man an Stelle von (7) üblicherweise


(9)

und nennt die Funktion W(r₁,r₂;ν) (=G⁽¹⁾(r₂,r₁;ν)) die wechselseitige spektrale Dichte der Lichtschwingungen an den Orten r₁ und r₂. Die Funktion W(r,r;ν)=G⁽¹⁾(r,r;ν) gibt das Frequenzspektrum der Strahlung (auch Leistungsspektrum oder spektrale Dichte genannt) an. Die Relation (7) bzw. (9) wird im Falle r₁=r₂Wiener-Khintchine-Theorem genannt. Sie lehrt, daß man spektrale Informationen auch (indirekt) durch Beobachtung räumlicher Interferenzen gewinnen kann. Auf diesem Prinzip beruht im besonderen die Fourier-Spektroskopie.

Während sich die konventionelle Optik mit der Messung der Korrelationsfunktion 1. Ordnung (bzw. deren Fourier-Transformierter) begnügen mußte, machte die Entwicklung der photoelektrischen Empfänger auch die Messung von Korrelationsfunktionen höherer Ordnung möglich. Damit wurden erstmals die Fluktuationseigenschaften der Strahlung der Messung zugänglich. Dies betrifft vor allem die Schwankungen der Intensität, über deren Verhalten die Intensitätskorrelationsfunktion oder Korrelationsfunktion 2. Ordnung


(10)

Auskunft gibt, wobei I(r,t)=E^(-)(r,t) E⁽⁺⁾(r,t) – von einem Vorfaktor abgesehen – die momentane Intensität bezeichnet. Die Messung von G⁽²⁾ beruht auf dem Umstand, daß der in einem Photodetektor erzeugte Photostrom – oder, im Falle von Photonenzählung (Photonenstatistik), die Zahl der jeweils in einem festen Zeitintervall registrierten Photonen – das zeitliche Verhalten der Intensität des auf den Detektor fallenden Lichtes widerspiegelt. Gemessen werden daher Korrelationen zwischen den Photoströmen zweier Photodetektoren oder den von ihnen registrierten Photonenzahlen, wobei auch eine Koinzidenzzähltechnik verwendet werden kann (Photonenstatistik). Die Pionierarbeit auf diesem Gebiet wurde in den fünfziger Jahren von R. Hanbury Brown und R.Q. Twiss mit der Schaffung eines neuartigen Sterninterferometers geleistet. Dabei geht es um die Messung räumlicher Korrelationen G⁽²⁾(r₁,r₂;0). Dagegen werden in der Photonenstatistik und der Photonenkorrelationsspektroskopie zeitliche Korrelationen G⁽²⁾(r,r;τ) untersucht.