Kristalloptik, ein spezielles Gebiet der Kristallphysik, beschreibt das optische Verhalten von Kristallen sowie die entsprechenden mathematischen und physikalischen Zusammenhänge. Die Kristalle des kubischen Kristallsystems sind ohne Berücksichtigung schwacher Effekte der räumlichen Dispersion isotrop, d.h., sie verhalten sich für das Licht in allen Richtungen gleichartig. Die Kristalle aller übrigen Kristallsysteme sind anisotrop, d.h., die optischen Eigenschaften sind abhängig von der Ausbreitungsrichtung des Lichtes (bezüglich der kristallographischen Achsen). Optische Anisotropie läßt sich auch durch synthetische Schichtsysteme erzeugen (Formdoppelbrechung). Alle Erscheinungen der K. werden durch die Maxwellschen Gleichungen beschrieben, wobei die Form der Materialgleichungen wesentlich ist. Inhrsotropen Medien sind der Vektor der dielektrischen Verschiebung D und der Vektor der elektrischen Feldstärke E zueinander parallel und hängen über die relative Dielektrizitätskonstante ε und die Dielektrizitätskonstante des Vakuums ε₀ in der Form D=ε₀εE miteinander zusammen. Im allgemeinen Falle eines anisotropen Mediums mit räumlicher Dispersion und optischer Nichtlinearität (nichtlineare Optik) sind D und E mittels eines nichtlokalen und nichtlinearen Funktionals miteinander verbunden, dessen Entwicklung bei Vernachlässigung magnetischer Effekte die folgende Form annimmt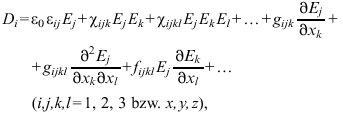


(1)

wobei über doppelt auftretende Indizes zu summieren ist. Die Summanden mit den zweiten und höheren Potenzen in E_i beschreiben die nichtlinearen Beiträge zu D, die mit den Ableitungen E_j/x_k entsprechen der räumlichen Dispersion.

Die klassische K. wird aus dem linearen Anteil von (1) D_i=ε₀ε_ijE_j oder, ausführlich geschrieben,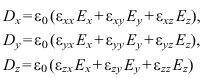


(2)

bei vorausgesetzter Parallelität zwischen der magnetischen Feldstärke H und der magnetischen Induktion B abgeleitet. Der symmetrische dielektrische Tensor ε_ij enthält maximal 6 verschiedene Komponenten, die in Kristallen mit vernachlässigbarer Absorption reell sind, und die sich in einem bestimmten, mit dem Kristalle verbundenen rechtwinkligen Koordinatensystem auf die drei Hauptdielektrizitätskonstanten

und

reduzieren. Die Achsen dieses Koordinatensystems heißen optische Symmetrieachsen. Dabei sind n_x, n_y und n_z die Hauptbrechungsindizes, aus denen die drei Hauptlichtgeschwindigkeiten c_x=c/n_x, c_y=c/n_y und c_z=c/n_z berechnet werden können, wobei c die Vakuumlichtgeschwindigkeit bedeutet.

Die Kristallsymmetrien haben entsprechende Symmetrieeigenschaften des ε-Tensors zur Folge. Für trikline Kristalle können wegen fehlender Symmetrie keine Aussagen über die Lage der optischen Symmetrieachsen bezüglich der kristallographischen Achsen gemacht werden. Monokline Kristalle dagegen besitzen genau eine Symmetrieebene, und in dieser Ebene müssen zwei der Symmetrieachsen liegen. Rhombische (genauer orthorhombische) Kristalle besitzen drei zueinander orthogonale kristallographische Achsen, und mit diesen fallen die Symmetrieachsen zusammen. Von den optischen Symmetrieachsen wohl zu unterscheiden sind die optischen Achsen oder Achsen der Isotropie. Sie sind dadurch definiert, daß zu den zugehörigen Richtungen (wie im isotropen Falle) nur eine Wellenausbreitungsgeschwindigkeit (Normalengeschwindigkeit, s.u.) gehört, so daß eine in Richtung einer optischen Achse sich ausbreitende Welle keine Doppelbrechung erfährt.

In all den genannten Fällen sind die drei Hauptbrechungsindizes voneinander verschieden. Die betreffenden Kristalle sind daher optisch zweiachsig (s.u.). Bei Kristallen des tri-, tetra- und hexagonalen Systems sind zwei der kristallographischen Achsen gleichwertig, entsprechend sind die zugehörigen Hauptbrechungsindizes gleich. Die zur Beschreibung der Lichtausbreitung im Kristalle verwendeten Flächen (s.u.) werden dadurch rotationssymmetrisch. Die Folge davon ist, daß die beiden optischen Achsen in eine zusammenfallen, die mit der Rotationsachse identisch ist. Die Kristalle sind optisch einachsig.

Aus den Maxwellschen Gleichungen ergibt sich bei Ausbreitung des Lichtes in Gestalt einer ebenen Welle A exp{-iω(t-(n/c)rn)} mit der Kreisfrequenz ω und der Wellennormalenrichtung (Einheitsvektor) n bei Vorliegen des (von n abhängigen) Brechungsindexes n für die mit dieser Welle verbundenen elektrischen und magnetischen Feldgrößen der in Abb. 1 dargestellte prinzipielle Zusammenhang.

Es zeigt sich, daß E, D, n und s=E×H/|E×H| in einer Ebene senkrecht zu B bzw. H liegen, wobei die Wellenfronten senkrecht zu n orientiert sind, die Energie jedoch parallel zum Poynting-Vektor E×H längs s transportiert wird. Dieser im allgemeinen auftretende Unterschied zwischen dem Wellennormalenvektor n und dem die Strahlrichtung anzeigenden Richtungsvektor s für den Energietransport (die für isotrope Medien zusammenfallen) ist wesentlich für die Phänomene der K. Die Ausbreitungsgeschwindigkeit c_s (Strahlgeschwindigkeit = Energietransportgeschwindigkeit = Gruppengeschwindigkeit) längs s steht (bei Vernachlässigung der Dispersion des Mediums) zur Ausbreitungsgeschwindigkeit c_n (Phasen- oder Normalengeschwindigkeit) längs n im Verhältnis


(3)

Dabei bezeichnet α den Winkel zwischen n und s bzw. E und D (Abb. 1), den sogenannten Anisotropiewinkel, der sich in Abhängigkeit von der Ausbreitungsrichtung im Kristalle ändert. Der zum Brechungsindex n=c/c_n analoge Strahlenindex wird durch s=c/c_s definiert. Meistens wird unter der Polarisationsrichtung die Richtung des D-Vektors, der senkrecht zu n schwingt, verstanden. Allerdings existiert in der K. eine "Dualität", wonach der Übergang von der "Wellenbeschreibung" zur "Strahlenbeschreibung" durch Austausch der Vektoren n und s, D und E und weiterer Größen möglich ist.

Anisotrope Kristalle zeigen die Erscheinung der optischen Doppelbrechung: Eine auf den Kristall einfallende Lichtwelle wird im allgemeinen in zwei Wellen zerlegt, die senkrecht zueinander linear polarisiert sind. Im Spezialfalle einachsiger Kristalle verhält sich eine dieser Wellen, die ordentliche Welle, entsprechend dem Snelliusschen Brechungsgesetz sinψ₁/sinψ₂=n_o (mit ψ₁ als Einfalls- und ψ₂ als Brechungswinkel), die andere, die außerordentliche Welle, zeigt eine sich mit ψ₁ ändernde Brechzahl n_e.

Es ist üblich, die verschiedenen Erscheinungen der Lichtausbreitung in Kristallen durch Konstruktionen an räumlichen Flächen zu veranschaulichen. Folgende 8 Fälle sind zu unterscheiden (Tab. 1):

Von einem Punkte im Kristalle ausgehend kann man fragen, wie weit das Licht in einem gegebenen Zeitintervall gelangt, und zwar einmal längs der Normalenrichtung n und zum anderen längs der Strahlrichtung s. Da zu jeder Welle zwei Polarisationsmöglichkeiten mit unterschiedlichen Geschwindigkeiten gehören, gibt es zu jeder Richtung zwei solche Endpunkte. Es ergeben sich so die beiden zweischaligen Flächen in Tab. 1, Spalte 3, Punkt 1 und 3. In einigen Darstellungen werden die Strahl- bzw. die Normalengeschwindigkeit in der betreffenden Richtung abgetragen, in anderen die entsprechenden reziproken Brechungsindizes. Da letztere den genannten Geschwindigkeiten proportional sind, unterscheiden sich die Flächen jeweils nur im Maßstabe.

Man kann auch die zu den Geschwindigkeiten reziproken Indizes (Brechungsindex bzw. Strahlenindex) vom Ursprunge aus auftragen; es entstehen so die Flächen in Spalte 3, Punkt 2 und 4. Anstelle der zweischaligen Flächen können auch entsprechende einschalige Flächen (Spalte 2) benutzt werden (s.u.). Letztere sind geometrisch einfacher, aber die für die Lichtausbreitung relevanten Größen (z.B. die Brechungsindizes) müssen aus der Schnittfigur der einschaligen Fläche mit einer Ebene senkrecht zur Ausbreitungsrichtung abgelesen werden (Abb. 6).

Das einfachste Modell zur Veranschaulichung der Wellenausbreitung in Kristallen ist die Huygenssche Strahlenfläche, auch Strahlengeschwindigkeitsfläche genannt. Diese Fläche gibt an, wie weit sich von einem Punkte im Inneren des Kristalles aus das Licht in einem gegebenen Zeitintervalle in den verschiedenen Raumrichtungen ausbreitet. (Aufgetragen wird die Strahlgeschwindigkeit in Strahlrichtung.) Für jede der beiden Polarisationsmöglichkeiten entsteht so eine Fläche, die die Wellenfront der entsprechenden Huygensschen Elementarwelle darstellt (Abb. 2). Bei einem isotropen Kristalle ist die Huygenssche Strahlenfläche eine Kugel. Bei einem optisch einachsigen Kristalle erhält man für die ordentlichen Wellen eine Kugel, für die außerordentlichen Wellen ergibt sich ein Rotationsellipsoid, das die Kugel in zwei Punkten berührt. Die durch diese beiden Punkte hindurchgehende Gerade ist also dadurch ausgezeichnet, daß sie die Strahlrichtung anzeigt, für welche die beiden Strahlgeschwindigkeiten übereinstimmen. Bei optisch einachsigen Kristallen fällt sie mit der optischen Achse zusammen, der definitionsgemäß die gleiche Eigenschaft bezüglich der Normalenrichtung und -geschwindigkeit zukommt.

Bei einem Kristallschnitt senkrecht zur optischen Achse und senkrechtem Lichteinfall erfolgt daher keine Strahlaufspaltung. Die Strahlgeschwindigkeiten für die ordentliche und die außerordentliche Welle und die beiden Normalengeschwindigkeiten sind einander gleich. Diese Aussage ist für zweiachsige Kristalle zu modifizieren (s.u.).

Bei positiv optisch einachsigen Kristallen umschließt die Kugel das Rotationsellipsoid (Abb. 2a), da die Strahlgeschwindigkeit der außerordentlichen Wellen – ausgenommen in Richtung der optischen Achse – kleiner ist als die der ordentlichen Wellen. Bei negativ optisch einachsigen Kristallen umschließt das Rotationsellipsoid die Kugel (Abb. 2b). Mit dieser Strahlenfläche kann die Doppelbrechung für (seitlich begrenzte) Strahlen an einem einachsigen optischen Kristalle leicht entsprechend Abb. 3 verstanden werden: Die Einhüllenden der ordentlichen und der außerordentlichen Elementarwellen ergeben die neuen Wellenfronten, und die Strahlrichtungen s der Wellen sind durch die Berührungspunkte der Wellenfronten mit den Elementarwellen bestimmt. Hierbei ist s_o die Strahlrichtung der ordentlichen Welle und s_e die der außerordentlichen. Die ordentliche Welle ist senkrecht, die außerordentliche parallel zu dem durch die Normalenrichtung gehenden Hauptschnitt polarisiert. Unter einem Hauptschnitt versteht man dabei generell eine durch eine optische Achse gehende oder ihr parallele Ebene. Wäre der Kristall in Abb. 3 senkrecht zur optischen Achse geschnitten, so träte keine Strahlaufspaltung ein. Während für die Wellennormalen ein, wenn auch modifiziertes, Snelliussches Brechungsgesetz formuliert werden kann (alle Ausbreitungsrichtungen liegen in der Einfallsebene), ist das im Falle der außerordentlichen Welle für die Strahlrichtung nicht möglich. Im allgemeinen liegt letztere nicht in der Einfallsebene, ausgenommen den Fall, daß die Einfallsebene ein Hauptschnitt ist.

Bei optisch zweiachsigen Kristallen ist die Strahlenfläche ein zweischaliges Gebilde mit Flächen 4. Ordnung. Die zu einer vorgegebenen Strahlrichtung s=(s_x, s_y, s_z) gehörigen zwei Werte der Strahlgeschwindigkeit c_s ergeben sich als die beiden Wurzeln der Gleichung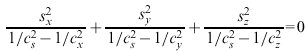


, (4)

wobei c_x, c_y und c_z die Hauptlichtgeschwindigkeiten bedeuten (s.o.). Abb. 4 zeigt die Schnitte der Strahlenfläche mit den Koordinatenebenen für den Fall, daß c_x<c_y<c_z (n_x>n_y>n_z) gilt. Daran ist abzulesen, daß es zwei Strahlausbreitungsrichtungen im Kristalle gibt, bei denen die Strahlgeschwindigkeiten für beide Polarisationsfälle (einer für jeder Schale) zusammenfallen. Sie werden als Biradialen bezeichnet.

Zur Erklärung von Interferenzphänomenen, bei denen die Strahlbegrenzungen meist keine Rolle spielen, ist es wichtiger, nicht die Strahlrichtungen s, sondern die Richtungen n der Wellennormalen zu betrachten. Trägt man die Wellennormalengeschwindigkeit c_n (Phasengeschwindigkeit) in Normalenrichtung n auf, so erhält man die ebenfalls zweischalige Normalenfläche. Die zu einer vorgegebenen Normalenrichtung n=(n_x, n_y, n_z) gehörigen, den beiden Polarisationsfällen entsprechenden Werte von c_n können dabei aus der Fresnelschen Normalengleichung


(5)

berechnet werden. Durch eine punktweise geometrische Konstruktion nach Abb. 5 kann die Normalenfläche aber auch aus der Strahlenfläche gewonnen werden: Man lege im Punkte P an die Strahlenfläche S die Tangentialebene T (Wellenfront mit der Normalen n, die zur Strahlrichtung s gehört) und fälle vom Ursprung das Lot auf T. Der Durchstoßpunkt Q des Lotes ist dann ein Punkt der Normalenfläche N. Letztere ist somit die "Fußpunktfläche" zur Strahlenfläche. Die zweite Schale der Strahlenfläche ist in dem in Abb. 5 gezeigten Schnitte ein Kreis, der durch die obige Konstruktion in sich übergeht. Die Existenz zweier Schalen der Strahlenfläche hat zur Folge, daß zu jedem gegebenen s im allgemeinen zwei n gefunden werden können. Umgekehrt gehören zu jedem gegebenen n zwei s.

Werden bei gegebenem n statt der beiden Wellennormalengeschwindigkeiten die entsprechenden Brechungsindizes direkt aufgetragen, so entsteht die für einachsige Kristalle in Abb. 2 gezeichnete zweischalige Indexfläche. Sie entspricht der Dispersionsbeziehung ω=ω(k) mit k als Wellenzahlvektor, die sich mit dem Ansatz einer ebenen Welle im Kristalle aus der Wellengleichung ergibt, und zwar gibt sie die aus der Dispersionsbeziehung bei festgehaltenem ω folgende Abhängigkeit des Betrages von k von der Ausbreitungsrichtung wieder. In Abb. 5 wäre sie einzuzeichnen als zweischalige Kombination aus Kreis und Ellipse, die S und N umschließt und anstelle von 1/n_x, 1/n_y, 1/n_z die Halbachsen n_x, n_y, n_z aufweist (vgl. Abb. 2).

Daß zur Veranschaulichung der kristalloptischen Erscheinungen statt der komplizierten zweischaligen Flächen einschalige Flächen, wie z.B. Ellipsoide, geeignet sind, wurde bereits von A. J. Fresnel gezeigt. Das Fresnelsche Ellipsoid erhält man, wenn man die beiden Strahlgeschwindigkeiten bzw. die durch die Division durch c daraus entstehenden reziproken Strahlenindizes nicht in Strahlrichtung s aufträgt, sondern senkrecht dazu in Richtung der elektrischen Feldstärkevektoren E für die beiden Polarisationsfälle. Für einachsige Kristalle ergibt sich ein Rotationsellipsoid, für zweiachsige Kristalle ein dreiachsiges Ellipsoid.

Geben wir anstelle der Strahlrichtung s nun die Normalenrichtung n für die Wellenausbreitung vor und tragen senkrecht zu n in Richtung der beiden möglichen Vektoren der dielektrischen Verschiebung D, d.h. der beiden Polarisationsrichtungen, die zugehörigen Brechungsindizes ab, so erhalten wir die in der K. am häufigsten verwendete Fletchersche Indikatrix (Abb. 6), auch Indexellipsoid, Normalenellipsoid oder Cauchysches Polarisationsellispoid genannt. Beschrieben wird dieses Ellipsoid durch die Gleichung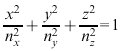


(6)

wobei n_x, n_y und n_z die Hauptbrechungsindizes bezeichnen (s.o.). Es ist wie das Fresnelsche Ellipsoid für einachsige Kristalle ein Rotationsellipsoid, für zweiachsige Kristalle ein dreiachsiges Ellipsoid. Werden die der Fletcherschen Indikatrix zugrunde liegenden Konstruktionen nicht mit dem Brechungsindex, sondern mit der dazu reziproken Wellennormalengeschwindigkeit durchgeführt, so ergibt sich als einschalige Fläche kein Ellipsoid, sondern ein Ovaloid 4. Grades.

Anhand der Fletcherschen Indikatrix kann man die wesentlichen Größen bei der Ausbreitung einer Welle in Normalenrichtung n sehr einfach nach Abb. 6 konstruieren: Wir schneiden die Indikatrix mit einer Ebene, die senkrecht zu n und durch das Zentrum verläuft. Die sich ergebende Schnittellipse S hat zwei Halbachsen, deren Längen die beiden Brechungsindizes n₁, n₂ darstellen, die ihrerseits die Ausbreitungsgeschwindigkeit der beiden möglichen, senkrecht zueinander polarisierten Wellen bestimmen. Deren D-Vektoren sind parallel zu der entsprechenden Halbachse der Schnittellipse gerichtet. Breitet sich das Licht speziell in Richtung einer der Halbachsen der Fletcherschen Indikatrix, also einer der optischen Symmetrieachsen (s.o.) aus, so liegen die D-Vektoren der beiden Teilwellen in Richtung der anderen beiden Halbachsen. In diesem Spezialfalle sind also die beiden Teilwellen in Richtung der optischen Symmetrieachsen polarisiert, weshalb deren Richtungen auch als Hauptschwingungsrichtungen bezeichnet werden. Bei optisch einachsigen Kristallen fällt die Rotationsachse der Indikatrix mit der optischen Achse des Kristalles zusammen. Wenn die rotationssymmetrische Indikatrix mit der Ebene senkrecht zu n gemäß Abb. 6 geschnitten wird, zeigt es sich, daß eine Halbachse der entstehenden Ellipse, also ein Brechungsindex n_o unabhängig von n immer denselben Wert hat, während der andere Brechungsindex n_e mit der Einfallsrichtung variiert. Der erste Brechungsindex bezieht sich daher auf die ordentliche, der zweite auf die außerordentliche Welle. Aus der in Abb. 6 erläuterten Konstruktion an der Indikatrix ergibt sich, daß die ordentliche Welle senkrecht zu dem durch n gehenden Hauptschnitte und die außerordentliche Welle in diesem Hauptschnitte schwingt. Die Polarisationsrichtung ist also auf sehr einfache Weise mit dem genannten Hauptschnitte verknüpft.

Ein Entartungsfall liegt vor, wenn n mit der Rotationsachse der Indikatrix zusammenfällt. Dann entartet die Schnittellipse zu einem Kreise, was bedeutet, daß der Polarisationszustand beliebig und der Brechungsindex (und damit auch die Normalengeschwindigkeit) stets der gleiche ist. Die Rotationsachse ist daher zugleich die optische Achse. Für eine Wellennormale senkrecht zur optischen Achse ergibt sich eine Schnittellipse, deren Halbachsen sich um den maximal erreichbaren Wert unterscheiden. Der Brechungsindex n_e für die außerordentliche Welle weicht also hier am weitesten vom Brechungsindex n_o der ordentlichen Welle ab. Bei positiv einachsigen Kristallen ist n_o<n_e und bei negativ einachsigen Kristallen ist n_o>n_e (optischer Charakter "+" oder "-"). Die Indikatrix hat für positiv einachsige Kristalle eine in Richtung der Rotationsachse langgestreckte Form, bei negativ einachsigen Kristallen ist die Ausdehnung in Richtung der Rotationsachse kürzer als der Durchmesser des Kreisschnittes.

Da n_o und n_e beide von der Wellenlänge λ abhängen, ist es auch möglich, daß ein Kristall je nach Spektralbereich positiv oder negativ einachsig sein kann. So ist z.B. der Kristall des Benzils (C₆H₅CO)₂ oberhalb von λ=420,2 nm positiv einachsig und darunter negativ einachsig.

Bei optisch zweiachsigen Kristallen ist die Indikatrix ein dreiachsiges Ellipsoid (Abb. 6). Die senkrecht zu beliebigen Wellennormalen durch das Zentrum der Indikatrix gelegten Schnitte sind im allgemeinen Ellipsen, nur zwei ausgezeichnete Richtungen von n führen zu Kreisen. Die zugehörigen Wellennormalenrichtungen kennzeichnen die beiden optischen Achsen. Sie werden auch als Binormalen bezeichnet. Für diese Richtungen tritt bei fehlender Absorption nur eine einzige Welle auf, deren Polarisationszustand beliebig sein kann. Die Winkelhalbierende des spitzen bzw. des stumpfen Winkels zwischen beiden Binormalen wird als spitze bzw. stumpfe Bisektrix bezeichnet oder auch als erste bzw. zweite Mittellinie. Der Winkel zwischen den optischen Achsen (der optische Achsenwinkel) 2V (Abb. 5) wird auch zur Charakterisierung der zweiachsigen Kristalle verwendet. Er berechnet sich für n_x>n_y>n_z aus der Beziehung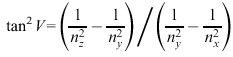


(7)

Ein zweiachsiger Kristall wird als positiv oder als negativ bezeichnet, je nachdem ob 2V ein spitzer Winkel (<90°) oder ein stumpfer Winkel (>90°) ist. Dies wird verständlich, wenn man in Abb. 5 beispielsweise V gegen Null gehen läßt. Dann wird die z-Achse zur optischen Achse eines Kristalles mit n_o=n_y=n_z<n_x=n_e, also eines positiv einachsigen Kristalles mit der optischen Achse entlang der Abszisse (vgl. Abb. 2). Die Biradialen und die Binormalen haben unterschiedliche Richtungen, denn der Winkel zwischen beiden Biradialen 2V_s (Abb. 5) bestimmt sich aus der Relation


(8)

Da die Untersuchung von Kristallen bevorzugt durch Interferenzen in Kristallen erfolgt und dafür die Wellennormalenrichtung n maßgeblich ist, wird der Begriff optische Achsen auf die Binormalen angewendet, während die Biradialen auch als Strahlenachsen oder sekundäre optische Achsen bezeichnet werden.

Zur Veranschaulichung der Doppelbrechung von Wellenfronten an einer Grenzfläche Luft-Kristall wird bevorzugt die Indexfläche verwendet, weil sie die im Kristalle zulässigen Wellenzahlvektoren k festlegt. An der Grenzfläche ist dafür zu sorgen, daß die Projektion des k-Vektors der einfallenden Welle gleich der Projektion des k-Vektors der beiden Wellenausbreitungsmoden auf die Grenzfläche wird. In Abb. 7 sind die mit 2π/λ₀ (λ₀ Vakuumwellenlänge) multiplizierten Indexflächen im Schnitt dargestellt, und zwar bedeutet S_i die Indexfläche für das isotrope Medium (Luft), S_o die Schale der Indexfläche für die ordentliche Welle im Kristalle und S_e die entsprechende Schale für die außerordentliche Welle. Der Wellenzahlvektor k_i der einfallenden Welle legt auf S_i den Punkt P_i fest, durch den die Normale N zur Grenzfläche G zu legen ist. Die Schnittpunkte von N mit S_e und S_o bestimmen die beiden Wellenzahlvektoren k_o und k_e, und die beiden Brechungsgesetze ergeben sich trigonometrisch aus dieser Konstruktion.

Aus den Werten für die Hauptbrechungsindizes kann über die daraus konstruierbaren o.g. Flächen das optische Verhalten der Kristalle vollständig beschrieben werden, wobei Temperatur- und Wellenlängenabhängigkeit unter Umständen berücksichtigt werden müssen. Bei merklicher Absorption treten zu den reellen Komponenten der ε_ik in (1) imaginäre Anteile hinzu (absorbierende Kristalle, Pleochroismus). In der Materialgleichung (1) sind mit ∂E_j/∂x_k die Effekte der räumlichen Dispersion und der optischen Aktivität, mit E_j E_k und E_j E_k E_l die Effekte der nichtlinearen Optik, aber auch die elektrooptischen Effekte verbunden. Können die Komponenten des ε-Tensors durch magnetostatische Felder beeinflußt werden, so liegen die magnetooptischen Effekte vor.

Die Anwendungen der K. umfassen die zum Umgange mit polarisiertem Lichte notwendigen Elemente wie Polarisatoren, aber auch Lichtmodulatoren und Bauelemente für die nichtlineare Optik. Grundsätzliche Untersuchungsmethoden der Kristallographie und Mineralogie beruhen auf den Erscheinungen der K. (Polarisationsmikroskop). In Tab. 2 sind Brechungsindizes verschiedener Kristalle aufgelistet.

Kristalloptik 1: Ausbreitung einer ebenen Welle in einem Kristalle. n Wellennormale, s Strahlrichtung, E elektrische Feldstärke, D dielektrische Verschiebung, H magnetische Feldstärke, B magnetische Induktion, W Wellenfronten, SB Strahlbegrenzung.

Kristalloptik 2: Schnitt durch die Huygenssche Strahlenfläche (--) in der Normierung c=1 und die Indexfläche (--) für einen positiv (a) (z.B. Quarz) und einen negativ (b) (z.B. Calcit) einachsigen Kristall. OA optische Achse, S Strahlenfläche, I Indexfläche, O und AO Schale für die ordentliche und außerordentliche Welle.

Kristalloptik 3: Huygenssche Konstruktion zur Beschreibung der Doppelbrechung an einem Kalkspatrhomboeder. AA ankommende, OO ordentliche und EE außerordentliche Wellenfront, o ordentlicher und e außerordentlicher Strahl, OA optische Achse.

Kristalloptik 4: Symmetrieebenen der Huygensschen Strahlenfläche eines zweiachsigen Kristalles. BR Biradialen, n_x, n_y, n_z Hauptbrechungsindizes, c Vakuumlichtgeschwindigkeit, V_S halber Winkel zwischen den Biradialen.

Kristalloptik 5: Zusammenhang zwischen Normalenfläche N und Strahlenfläche S in der Normierung c=1 für einen zweiachsigen Kristall mit n_x>n_y>n_z (Hauptbrechungsindizes). BR Biradiale, BN Binormale, s Strahl-, n Normalenrichtung, V bzw. V_S halber Winkel zwischen den Binormalen bzw. Biradialen.

Kristalloptik 6: Fletchersche Indikatrix mit Konstruktion der Brechungsindizes und der Richtungen der dielektrischen Verschiebung D. S Schnittellipse, n Richtung der Wellennormale, n₁ usw. Brechungsindizes.

Kristalloptik 7: Hamiltonsche Konstruktion für die Brechung an einem negativ einachsigen Kristalle. S_o und S_e Indexflächen des Kristalles, S_i Indexfläche des Außenmediums (Luft), G Grenzfläche, N Normale dazu, OA optische Achse, k_i usw. Wellenzahlvektor.