mikroskopische Abbildung, Erzeugung eines vergrößerten Bildes eines Objektes, dessen Einzelheiten mit bloßem Auge nicht wahrnehmbar bzw. nicht auflösbar sind, mit Hilfe eines Mikroskops. Die Beschreibung der m. A. kann nicht nur rein strahlenoptisch erfolgen, es muß vielmehr infolge des maßgeblichen Einflusses der Beugung die wellenoptische Betrachtung hinzugenommen werden.

1) Strahlengang im Mikroskop. Im Gegensatz zur vergrößernden Abbildung einer Lupe, die gelegentlich auch als "einfaches Mikroskop" bezeichnet wird, ist die Abbildung im zusammengesetzten Mikroskop zweistufig. Die Abbildung erfolgt im einfachsten Falle durch Objektiv und Okular (Abb. 1a). Sie sind dabei so angeordnet, daß das vom Objekt OB erzeugte umgekehrte, vergrößerte Zwischenbild O'B' in der vorderen Brennebene des Okulars liegt. Das Strahlenbündel, das die Abbildung des außeraxialen Objektpunktes B bewirkt, verläßt das Okular als paralleles Strahlenbündel. Ein auf Unendlich akkommodiertes Auge sieht den außeraxialen Bildpunkt in Richtung B″ liegen, während der axiale Bildpunkt in Richtung der optischen Achse gesehen wird. Die vergrößernde Wirkung des Mikroskops ist durch den Winkel bestimmt, den das ins Auge einfallende Parallelbündel mit der optischen Achse bildet.

Die Augenpupille befindet sich etwa am bildseitigen Brennpunkt F'_Mikr des Mikroskops, der der Schnittpunkt aller im Objektraum parallel einfallenden Hauptstrahlen ist (Mikroskopbeleuchtung). Diese Stelle engster Einschnürung aller an der m. A. beteiligten Strahlenbündel ist die Austrittspupille AP des Mikroskops (auch "Augenkreis" oder "Ramsdenscher Kreis" genannt). Der Abstand von der bildseitigen Brennebene des Objektivs bis zur objektseitigen Brennebene des Okulars wird als optische Tubuslänge t bezeichnet; sie ist für die Mikroskopvergrößerung bedeutsam und von der mechanischen Tubuslänge zu unterscheiden. Aufgrund vieler Vorteile – insbesondere in der Auflicht- und Polarisationsmikroskopie – findet in neuzeitlichen Mikroskopen mehr und mehr die Unendlich-Optik Anwendung (Abb. 1b). Von einem Objekt OB wird das umgekehrte, vergrößerte Zwischenbild O'B' durch ein Objektiv mit unendlicher Bildweite und eine nachgeordnete Tubuslinse erzeugt, wobei der Abstand zwischen Objektiv und Tubuslinse innerhalb gewisser Grenzen frei wählbar ist, ohne daß dadurch die Lage des Zwischenbildes bezüglich der Tubuslinse oder die Größe des Zwischenbildes beeinflußt wird.

2) Vergrößerung des Mikroskops. Bei Objektiven mit endlicher Bildweite (Abb. 1a) ergibt sich die Vergrößerung Γ

des Mikroskops aus dem Produkt des Abbildungsmaßstabes des Objektivs

und der Vergrößerung des Okulars Γ

:Γ

=β

Γ

.

Mittels der Brennweiten von Objektiv f

_bj und Okular f

_k sowie der optischen Tubuslänge t kann die Mikroskopvergrößerung auch durch folgende Gleichung ausgedrückt werden: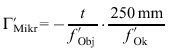

wobei die genannten Größen in mm anzugeben sind.

Bei Objektiven mit unendlicher Bildweite (Abb. 1b) ist bei der Vergrößerung des Mikroskopes noch ein Tubusfaktor q_Tub zu berücksichtigen, der vom Hersteller angegeben wird. Es gilt Γ

=Γ

q_TubΓ

.

Der optische Aufbau nach Abb. 1b entspricht der Abbeschen Zerlegung des zusammengesetzten Mikroskops in ein Objektiv mit Lupenwirkung und in ein Fernrohr. Die spezifische Aufgabe des Objektivs besteht in der Änderung der Divergenz von Strahlenkegeln großen Öffnungswinkels. Die Wirkung der nachgeordneten Optik entspricht der eines Fernrohres, wobei die spezifische Okularwirkung auf der Richtungsänderung von engen Strahlenbündeln beruht.

Um die Leistungsfähigkeit des Mikroskops hinsichtlich des Auflösungsvermögens (s.u.) voll auszunutzen, ist eine Mindestvergrößerung erforderlich. Andererseits ist es nicht zweckmäßig, die Vergrößerung des Mikroskops beliebig groß zu wählen, weil oberhalb einer bestimmten Vergrößerung keine weiteren Struktureinzelheiten sichtbar gemacht werden können. Nach E. Abbe liegt der Bereich der nutzbaren oder förderlichen Vergrößerung des Mikroskops etwa zwischen dem 500- und 1000fachen der (objektseitigen) numerischen Apertur A des Mikroskopobjektivs. Innerhalb dieses Bereiches werden die an der Auflösungsgrenze liegenden Objekteinzelheiten im Mikroskop deutlich getrennt gesehen, und zwar an der unteren bzw. oberen Grenze der förderlichen Vergrößerung unter einem Sehwinkel von 4' bzw. 2'. Zwischen dem Durchmesser d_AP der Austrittspupille des Mikroskops, der numerischen Apertur A und der Mikroskopvergrößerung Γ

besteht der Zusammenhang d_AP=-500A/Γ

. Die untere Grenze der förderlichen Vergrößerung, bei der gemäß dieser Gleichung die Austrittspupille einen Durchmesser von 1 mm hat, bezeichnet man auch als Normalvergrößerung. Als leere Vergrößerung wird die über die obere Grenze der förderlichen Vergrößerung hinausgehende Vergrößerung bezeichnet. Ihr ist ein Austrittspupillendurchmesser von 0,5 mm zugeordnet. In besonderen Fällen kann Übervergrößerung angewendet werden, z.B. um Objekte zu zählen. Doch sind dabei folgende Nachteile zu beachten: Abnahme der Bildhelligkeit mit dem Quadrat des Austrittspupillendurchmessers, Zunahme von Störungen durch entoptische Erscheinungen und Unsauberkeiten besonders im Okularbereich, Minderung des Kontrastes sowie mangelnde Konturschärfe.

3) Wellenoptische Abbildung von Selbstleuchtern: Auflösungsgrenze. Die geometrische Optik erklärt wohl die m. A. in großen Zügen, aber zur Beschreibung von feineren Einzelheiten, was z.B. die Entstehung des mikroskopischen Bildes oder das Auflösungsvermögen des Mikroskops angeht, muß man die wellenoptische Betrachtungsweise heranziehen, d.h. die Gesetze der Interferenz und Beugung. Ein leuchtender Punkt, z.B. realisiert als kleine Öffnung in einer dünnen Metallschicht (Sterntest) wird wegen der Wellennatur des Lichtes als Beugungsfigur abgebildet, die aus einem hellen zentralen Scheibchen besteht, das von abwechselnd dunklen und hellen Ringen umgeben ist, deren Helligkeit nach außen stark abnimmt (Airy-Scheibchen).

Ein selbstleuchtendes Objekt kann man sich in einzelne leuchtende Punkte zerlegt denken. Da die von den einzelnen Punkten ausgehenden Wellen nicht kohärent sind, interferieren sie nicht miteinander, so daß im Bilde die Intensitäten (Beleuchtungsstärken) der einzelnen Beugungsfiguren an den Stellen, wo sie sich überlappen, zu summieren sind. Man spricht in diesem Falle von inkohärenter Abbildung. Sie bildet bei der m. A. die Ausnahme. Jedoch gibt es auch in der Mikroskopie wichtige Anwendungen der inkohärenten Abbildung. So können die fluoreszierenden Objekte in der Fluoreszenzmikroskopie und die Infrarotstrahlung emittierenden Objekte der Emissions-IR-Mikroskopie als "Selbstleuchter" aufgefaßt werden. Weiterhin ist die inkohärente Abbildung die Grundlage für die beugungstheoretische Bewertung der Bildgüte bei der m. A. (Definitionshelligkeit).

Zwei leuchtende Objektpunkte erscheinen als vollständig getrennt, wenn zwischen den beiden zentralen Beugungsscheibchen der den Objektpunkten zugeordneten Beugungsfiguren ein absolutes Minimum mit der Intensität Null liegt (Grenze der totalen Auflösung). Erfahrungsgemäß werden jedoch zwei benachbarte Bildpunkte auch dann noch als getrennt wahrgenommen, wenn sie sich zum Teil überdecken, so daß das dazwischenliegende relative Minimum etwa 80% der im Zentrum des Beugungsscheibchens vorhandenen Intensität beträgt. Das ist der Fall, wenn das Zentrum des einen Beugungsscheibchens auf das erste Minimum bzw. den ersten dunklen Ring des zweiten Beugungsscheibchens fällt. Selbstleuchtende Objektpunkte werden danach gerade noch getrennt abgebildet, wenn ihr Abstand d≥0,61λ/A ist (Rayleigh-Auflösungsvermögen für den Kohärenzparameter S=1, Auflösungsvermögen 1)), wobei A die numerische Apertur und λ die Wellenlänge bezeichnen.

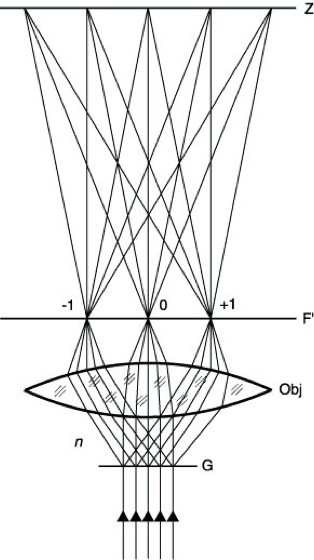
4) Wellenoptische Abbildung von Nichtselbstleuchtern: Auflösungsgrenze. Zur Erklärung der m. A. bei nichtselbstleuchtenden Objekten (Abbesche Theorie des Mikroskops) ging E. Abbe (1840 bis 1905) von strukturierten Objekten aus, insbesondere von solchen mit periodischen Strukturen. Im einfachsten Falle betrachtete er ein Gitter (ein Objekt mit regelmäßiger Streifung) mit der Gitterkonstante d, das von parallelem kohärenten Licht durchstrahlt wird (Abb. 2). Zur Erzeugung dieses Lichtbündels dient z.B. eine nahezu punktförmige Lichtquelle im vorderen Brennpunkt eines nicht dargestellten Kondensors. Die Spalten des Gitters sind nach dem Huygensschen Prinzip Ausgangsort kohärenter Wellen, die sich überlagern und infolge von Interferenz in Abhängigkeit von der Ausbreitungsrichtung verstärkt oder geschwächt werden. In den Richtungen, die durch die Bedingung dnsinσ/λ=0, 1, 2, ... festgelegt sind (Beugungsgitter), ergibt sich durch Interferenz Helligkeit; in den dazwischen liegenden Richtungen erhält man dagegen Dunkelheit. Dabei bezeichnen σ den Winkel zwischen der optischen Achse und der Strahlrichtung maximaler Helligkeit, n die Brechzahl des hinter dem Gitter befindlichen Mediums und λ die Wellenlänge des benutzten Lichtes in Luft. In der bildseitigen Objektivebene entstehen daher Beugungsbilder (primäres Interferenzbild) 0-, ±1-, ±2-, ...ter Ordnung der Lichtquelle. Die Zahl der in der Objektivöffnung erscheinenden Maxima hängt ab von der numerischen Apertur A=nsinσ des Objektivs, von der Wellenlänge des Lichtes und der Gitterkonstante des Objekts. Das in der Bildebene des Objektivs entstehende Zwischenbild, das durch das Okular beobachtet wird, ist von der Beugungserscheinung in der Brennebene des Objektivs abhängig und entsteht als sekundäre Interferenzerscheinung. Die Struktur des Objekts wird getreu wiedergegeben, wenn alles von diesem gebeugte Licht vollständig zur Wirkung gelangt. Damit überhaupt ein Bild zustande kommt, müssen mindestens zwei Beugungsmaxima durch das Objektiv hindurchtreten, da zur Interferenz wenigstens zwei Anteile nötig sind. Kommt durch Abblenden der anderen nur das Beugungsbild 0ter Ordnung zur Wirkung, dann ist es hinsichtlich der Abbildung genauso, als wenn kein Objekt vorhanden wäre. Eine Abnahme der Zahl der zur Wirkung kommenden Maxima verringert also die Objektähnlichkeit des Bildes. Feine Objektstrukturen beugen das Licht so stark, daß es am Objektiv vorbeigeht und nicht zur Abbildung beitragen kann.

Die Auflösungsgrenze beim Gitter ist dann erreicht, wenn gerade noch zwei benachbarte Maxima des primären Beugungsbildes von der Objektivöffnung zum Bildaufbau zugelassen werden. Das ist bei senkrecht einfallendem Licht (Abb. 2) für d=λ/A der Fall. Bei schief einfallendem Licht (Mikroskopbeleuchtung) gilt d = λ/(2A). Bei Beleuchtung mit einer ausgedehnten Lichtquelle liegt die Auflösungsgrenze zwischen λ/A und λ/(2A).

Durch gezielte Eingriffe in das primäre Interferenzbild (Fourier-Transformation in der Optik) kann die m. A. stark verändert werden, wie dies z.B. beim Phasenkontrastverfahren geschieht.

Eine moderne Ausgestaltung und Weiterentwicklung hat die Abbesche Theorie der Bildentstehung im Mikroskop durch die Anwendung der Fourier-Transformation erfahren. Sie bildet das mathematische Rüstzeug, um auf der Grundlage der partiell kohärenten Abbildung, d.h. bei üblichen Beleuchtungsaperturen A_Bel, die kleiner sind als die numerische Apertur A_Obj des Objektivs, beliebig gestaltete Objekte in ihrem Abbildungsverhalten theoretisch zu untersuchen. Es hat sich herausgestellt, daß die seit langem in der praktischen Mikroskopie übliche Regel, die Beleuchtungsapertur als 2/3 A_Obj zu wählen, durch die Theorie der partiell kohärenten Abbildung für die meisten Anwendungsfälle als zweckmäßig bestätigt wird.

5) Schärfentiefe. Bei der Scharfeinstellung eines mikroskopischen Präparates ergibt sich ein gewisser Spielraum, den man als Einstellungenauigkeit oder auch als Schärfentiefe auffassen kann. Die Schärfentiefe bei der m. A. kommt zustande durch die axiale Ausdehnung der Beugungserscheinung des mikroskopischen Bildes (wellenoptische Schärfentiefe t_w) und den bildseitig zulässigen Unschärfekreis (geometrisch-optische Schärfentiefe t_g), bedingt durch die begrenzte Auflösung des Auges oder eines anderen Empfängers, und durch die Fähigkeit des Auges zu akkommodieren (Akkommodationstiefe t_a). Der Einfluß der Akkommodation kann dadurch ausgeschaltet werden, daß in der Brennebene des Okulars eine Strichmarkierung angeordnet wird, die gleichzeitig mit dem Objekt scharf gesehen werden muß. Die wellenoptische Schärfentiefe t_w=nλ/A² ist nur von der numerischen Apertur A des Objektivs abhängig und sinkt mit steigender Apertur stark ab. Hochaperturige Objektive haben deshalb sehr geringe Schärfentiefe, jedoch hohes Tiefenauflösungsvermögen (Auflösungsvermögen).

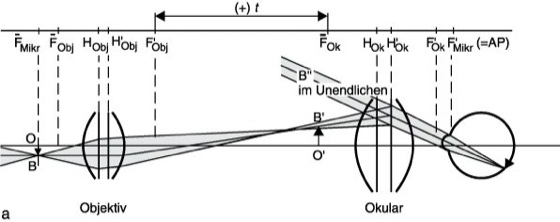
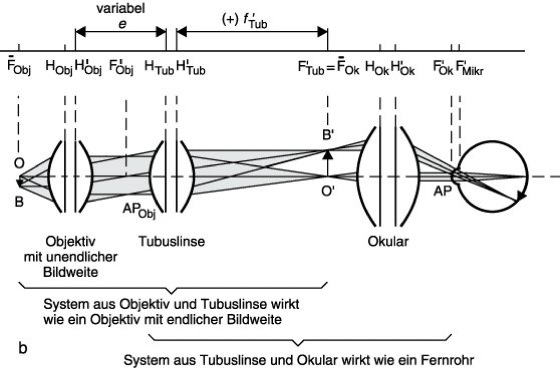
Mikroskopische Abbildung 1: Abbildungsstrahlengang im zusammengesetzten Mikroskop bei Mikroskopobjektiven mit endlicher (a) und unendlicher (b) Bildweite.

, F' Brennpunkte, f' Brennweite; H, H' Hauptebenen, t optische Tubuslänge, AP Austrittspupille.

Mikroskopische Abbildung 2: Zur Abbeschen Theorie des Mikroskops. G Gitter, Obj Objektiv, F' hintere Brennebene des Objektivs, Z Zwischenbildebene, n Brechzahl.