Optikmodellierung, ein wesentlicher Teil der konstruktiven Optik, die den Entwurf und die Optimierung optischer Systeme sowie deren Produktionsbetreuung aus konstruktiver Sicht umfaßt. Zu einem geforderten optischen System werden in der O. alle geometrischen und alle Materialparameter einschließlich ihrer Toleranzen berechnet. Die Technologie der Modellierung basiert auf mathematischen Funktionsmodellen, mit deren Hilfe im numerischen Experiment auf Computern die Eigenschaften eines optischen Systems bestimmt werden. Grundlage der Algorithmen sind die Gesetze der Lichtausbreitung und der Wechselwirkung des Lichtes mit strukturierten Medien. Dabei wird eine zeitfreie skalare Wellentheorie zur Beschreibung der Lichtausbreitung verwendet.

Der Prozeß der O. gliedert sich in die Phasen der Ansatzbildung, der Optimierung, der Produktionsvorbereitung und der Produktionsbetreuung.

a) Die Ansatzphase beinhaltet die Auswahl eines Startsystems für die Lösung einer gegebenen Aufgabenstellung. In der Regel versucht der Optikmodellierer, geleitet von seiner Erfahrung und grundsätzlichen Kenntnissen über Typeigenschaften, aus einem Archiv vorhandener Lösungen für optische Systeme einen geeigneten Typ auszuwählen. Die Typauswahl stellt einen entscheidenden Schritt zur Aufgabenlösung dar.

Grundsätzliche Bedeutung haben dabei paraxiale Beziehungen, mit denen charakteristische Abbildungsverhältnisse, z.B. der Abbildungsmaßstab, die Haupt-, Knoten- und Brennpunktlagen fixiert werden. Außerdem spielen hierbei einfache Näherungen zur Beschreibung der Abbildungsfehler wie Öffnungsfehler, Koma, Astigmatismus, Bildfeldwölbung, Verzeichnung und chromatische Fehler eine wichtige Rolle.

b) In der Optimierungsphase versucht man, mit einem gewählten Ansatz zur Lösung der gestellten Aufgabe zu gelangen. Methodisch stehen heute dafür hochentwickelte CAD-Systeme zur Verfügung. Da es sich um nichtlineare Vektoroptimierung handelt, kann die Optimierung nur schrittweise in einem ständigen Dialog zwischen Optikmodellierer und Computer erfolgreich vorgenommen werden. Oftmals sind auch taktische Maßnahmen am Systemaufbau, z.B. das Aufspalten einer Linse, seitens des Optikmodellierers sinnvoll, um den Optimierungsprozeß zu beschleunigen oder überhaupt weiterzubewegen. Auch die Wahl der in die Optimierung einzubeziehenden Systemparameter obliegt dem Optikmodellierer. Er kann damit ebenfalls wesentlich auf den Erfolg eines Optimierungsverfahrens bei einer konkreten Aufgabenstellung einwirken.

c) In der Produktionsvorbereitungsphase wird – ausgehend von einem optimierten optischen System, das die optischen, konstruktiven und wesentliche technologische Bedingungen erfüllt – eine Tolerierung aller Fertigungs- und Materialparameter vorgenommen. Die Festlegung der Toleranzen ist selbst ein Optimierungsproblem, wobei als Kriterium die minimalen Produktionskosten, bei Sicherung der optischen Leistung des Systems, fungieren. Durch Vorsehen von Justierparametern im optischen System kann das zulässige Toleranzvolumen vergrößert werden.

d) Die Produktionsbetreuung durch O. wird erforderlich bei Tolerenzen, die material- oder bearbeitungsseitig nicht ohne weiteres eingehalten werden können. Beispielsweise können die Brechzahlwerte von Glasschmelze zu Glasschmelze sich so stark ändern, daß eine Nachoptimierung auf der Basis der Schmelzmeßwerte für das optische System gerechnet werden muß. Ein anderer typischer Fall sind Abweichungen der Linsenmittendicken oder Zentrierungen über die zulässige Toleranz hinaus. Hier kann durch individuelle Paarungs- und Justiervorschrift für die Montage der Optikteile eine erhöhte Gutausbeute an optischen Systemen erreicht werden. Das Durchrechnen solcher Paarungs- und Justiervorschriften kann im voraus für angenommene Toleranzüberschreitungen erfolgen. Bei Hochleistungsoptiken erfolgt die Durchrechnung in der O. anhand der konkreten Meßwerte pro Teil, und es ergeben sich so für jedes optische System individuelle Montagevorschriften.

Grundlage für alle Berechnungen in der O. ist die Durchrechnung von Stützstrahlen durch das optische System (Strahldurchrechnung) sowie die Interpolation der Wellenfläche aus diesen Strahlen im Bildraum. Die Abb. veranschaulicht das grundsätzliche Vorgehen. Für jeden isoliert betrachteten Objektpunkt Q wird ein Strahlenbündel unter Berücksichtigung der Symmetrieverhältnisse generiert. Bei rotationssymmetrischen optischen Systemen genügt es in der Regel, die Stützstrahlen in meridionaler und sagittaler Richtung zu bilden. Die Stützungsvorschrift (Wahl der Anzahl und Lage der Stützungspunkte in der Eintrittspupille) stellt meistens einen Kompromiß aus optischen und mathematischen Überlegungen dar. Mit der Strahldurchrechnung fallen die Wellenaberrationen punktweise an der Bezugskugel des Bündels um den Aufpunkt Q' an. Dies ist eine Kugel mit einem sinnvoll gewählten (grundsätzlich beliebigen) Radius, auf der die optische Weglänge des Bündelstrahls definitionsgemäß einen konstanten Wert besitzt. Die Wellenaberration wird als Differenz der optischen Weglängen von Bündel- und Bezugsstrahl definiert. Aus den punktweise berechneten Wellenaberrationen kann dann durch Interpolation die gesamte Wellenaberration, und damit auch die Wellenfläche, bestimmt werden. Die Wellenaberration wird dabei meist als eine Reihenentwicklung nach den Zernikeschen Kreispolynomen angesetzt.

Eine andere Möglichkeit der Bestimmung der Wellenaberration beruht auf der Berechnung der Queraberrationen. Darunter versteht man die Abweichungen der Punkte, in denen die Bündelstrahlen die Gaußsche Bildebene durchstoßen, vom Gaußschen Bildpunkt. Aus ihnen lassen sich im Falle eines rotationssymmetrischen optischen Systems die ersten partiellen Ableitungen der Wellenaberration nach den Polarkoordinaten ρ und ϕ punktweise berechnen und daraus die Wellenaberration selbst.

e) Die Bewertung des erreichten Systemzustandes stellt sich dem Optikmodellierer als zentrale Aufgabe während des gesamten Modellierungsprozesses. Die Bewertung der optischen Leistung (optische Bewertung) hat Vorrang gegenüber der konstruktiven, der technologischen und der ökonomischen Bewertung. Sie liefert Aussagen über die Abbildungsqualität eines Systems. Aufgrund der großen Differenziertheit in den Qualitätsansprüchen an optische Systeme steht dem Optikmodellierer ein umfangreiches Spektrum an optischen Bewertungsfunktionen zur Verfügung, aus dem er je nach Aufgabenstellung einen passenden Bewertungsvektor zusammenstellt. Bei noch nicht optimierten optischen Systemen, also im Ansatzstadium, ist es wenig sinnvoll, wellenoptische Bewertungskriterien wie z.B. die Definitionshelligkeit oder das wellenoptische Gauß-Moment anzuwenden. Traditionell wird hier einfach mit Queraberrationen gearbeitet und z.B. im Sinne eines minimalen Zerstreuungskreises der Queraberrationen eine Optimierung pro Bildpunkt vorgenommen. Noch weniger rechenaufwendig ist die Anwendung der klassischen Seidelschen Bildfehlertheorie. Sie liefert Näherungsformeln für die geometrisch bedingten Aberrationen an optischen Systemen. Außerdem gibt sie mit den Flächenteilkoeffizienten Auskunft über innere Widersprüche in einem System und eignet sich daher eigentlich sehr gut zur Unterstützung konstruktiver Überlegungen beim Entwurf optischer Systeme. Ihre Anwendung unterliegt jedoch der einschneidenden Beschränkung auf den achsnahen Raum. Diese Schwäche konnten auch Bildfehlertheorien höherer Ordnung nicht überwinden. Wesentlich besser eignet sich hier die geometrische Grundbewertung nach Wartmann, die eine Verallgemeinerung der Seidel-Theorie für außeraxiale Bildpunkte darstellt. Sie hat den Vorzug der einfachen, schnellen Berechenbarkeit sowie der Gültigkeit für beliebig schlechte optische Systeme. Zugleich ermöglicht sie einen reibungslosen Übergang zu wellenoptischen Kriterien in einem fortgeschrittenen Optimierungsstadium.

Moderne Hochleistungssysteme können nur mittels wellenoptischer Bewertungskriterien im Endstadium der Optimierung erreicht werden. Die in der O. heute wichtigsten sind die Definitionshelligkeit, der relative Bildkontrast und das wellenoptische Gauß-Moment. Während sich die Definitionshelligkeit besonders für die Optimierung beugungsbegrenzter optischer Systeme eignet, bildet der relative Bildkontrast ein wirksames Kriterium für Mittelklasse-Optik, z.B. Bildmeßobjektive. Das wellenoptische Gauß-Moment eignet sich für Systeme, die nur niedrige Ortsfrequenzen übertragen. Für Analysezwecke, insbesondere im Endstadium der O., ist es erforderlich, die wellenoptischen Kriterien für ein konkretes optisches System mit höherer Genauigkeit zu berechnen. Ein wesentliches Kriterium stellt die optische Übertragungsfunktion dar. Sie kann einmal über die Fourier-Transformation der Punktbildverwaschungsfunktion berechnet werden. Diese Methode eignet sich für optische Systeme mit hohem Auflösungsvermögen bei gleichzeitiger Forderung nach hohem Kontrast. Andererseits bewährt sich die Methode der Berechnung der optischen Übertragungsfunktion über das Duffieux-Integral der Pupillenfunktion. Das gilt insbesondere für optische Systeme im niedrigen Ortsfrequenzbereich.

Die Berechnung konstruktiver und technologischer Bewertungsfunktionen erweist sich in der Regel einfacher als die der optischen Bewertungsfunktionen. Die Einbeziehung der ökonomischen Bewertungsfunktionen in die O. bereitet heute oft noch Schwierigkeiten, da die funktionellen Zusammenhänge zwischen Kosten und Systemparametern eine sehr komplexe Beschreibung des Systems verlangen, die weit über das hinausgeht, was in der O. im engeren Sinne benötigt wird.

Für die Steuerung der Optimierungsverfahren ist es notwendig, die einzelnen Komponenten des Bewertungsvektors im Verhältnis zueinander zu wichten. Die Struktur der Steuerfunktion für die Optimierung hat im allgemeinen die Form der gewichteten Quadratsumme der Differenzen zwischen Bewertungs- und Zielkomponenten. Das Optimierungsproblem besteht dann darin, das Minimum der Steuerfunktion unter der durch die konstruktiven und technologischen Restriktionen gegebenen Nebenbedingung zu finden.

Bei den nichtlinearen Vektoroptimierungsverfahren lassen sich zwei Gruppen unterscheiden, die in der O. erfolgreich zur Anwendung gelangen: die Ableitungsverfahren und die ableitungsfreien Verfahren. Die erste Gruppe basiert auf der angenäherten Lösung der Minimumsforderung mittels einer Gaußschen Normalgleichung, in der Ableitungsmatrizen von m Bewertungskomponenten nach n Optimierungsvariablen auftreten. Typische Werte für m liegen bei 100 und darüber, für n bei 30 und mehr. Mit diesem Gauß-Newton-Verfahrenstyp werden stets nur lokale Minima der Steuerfunktion erreicht. Das Verfahren ist auch unter dem Namen "Methode der kleinsten Quadrate mit Dämpfung" oder DLS-Verfahren (DLS Abk. für engl. damped least square, "gedämpfte kleinste Quadrate") bekannt. Es wurde für die praktischen Anwendungen in der O. entwickelt. Als ein Vertreter der Gruppe der ableitungsfreien Verfahren kann das stochastische Simplexverfahren genannt werden, bei dem Startpunkte ausgewürfelt werden. Es zeichnet sich im Gegensatz zum DLS-Verfahren durch eine globalisierte Suche im Funktionsgebirge der Bewertung aus und eignet sich so in erster Linie für die Suche alternativer Systemansätze, die ihrerseits dann mit dem DLS-Verfahren weiter zu optimieren sind.

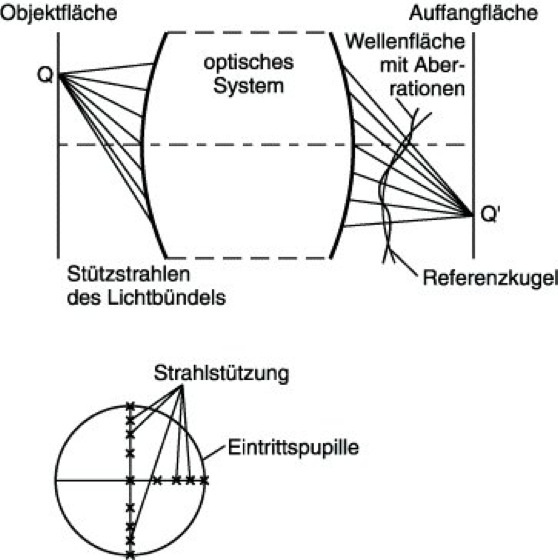
Optikmodellierung: Berechnung der Wellenfläche für die Abbildung Q – Q'.