optische Aktivität, optisches Drehvermögen, Drehung der Polarisationsebene, Rotationspolarisation, Gyration; eine von F. Arago 1811 am Quarz und von J. B. Biot 1815 an Zucker und Terpentin festgestellte Eigenschaft bestimmter Substanzen, die Polarisationsebene linear polarisierten Lichtes bei dessen Durchgange zu drehen. Die Drehung ist proportional zur durchstrahlten Länge. Neben der natürlichen o. A. kann eine o. A. auch erst durch äußere Magnetfelder hervorgerufen werden (Faraday-Effekt).

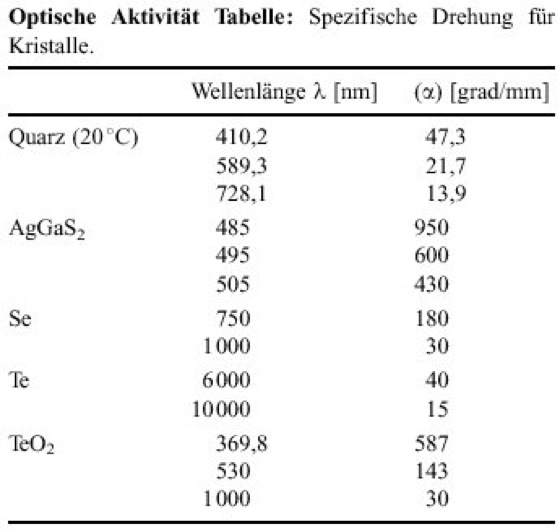
Die Ursache der o. A. liegt bei Kristallen in einer schraubenförmigen Kristallstruktur (Kristallsymmetrien ohne Symmetriezentrum) und bei Flüssigkeiten und Lösungen in einer Schraubenstruktur der Moleküle (ebenfalls ohne Symmetriezentrum) selbst. Eine schraubenförmige Kristallstruktur wurde in der Reuschschen Glimmerkombination, auch Glimmersäule genannt (E. Reusch 1869) durch eine wendeltreppenartige Anordnung von nicht drehenden, aber natürlich doppelbrechenden Glimmerplättchen nachgebildet und damit eine Rotationspolarisation erzeugt. Bei Flüssigkeiten und Lösungen ist nach van't Hoff und le Bel die o. A. an eine asymmetrische Molekülform gebunden. Beispielsweise ist in Abb. 1 ein asymmetrisches Kohlenstoffatom dargestellt, bei dem die nach den Ecken eines regulären Tetraeders gerichteten Valenzen des C-Atoms durch vier verschiedene Atome oder Radikale abgesättigt werden. Da zwei spiegelbildliche Formen des Moleküls existieren, die nicht durch Drehung ineinander überführt werden können (optische Isomerie), wird von beiden Formen eine unterschiedliche Drehung der Polarisationsebene hervorgerufen.

Zur theoretischen Beschreibung der o. A. im Rahmen der Maxwellschen Gleichungen ist in der Materialgleichung ein der räumlichen Ableitung der elektrischen Feldstärke E proportionaler Beitrag zur dielektrischen Verschiebung D – das bedeutet die Berücksichtigung der Verhältnisse an z.B. 10^-9 bis 10^-10 m entfernten Nachbarpunkten (z.B. an den Nachbaratomen) des Mediums – (Kristalloptik) in Betracht zu ziehen, d.h., es ist zu schreiben


(1)

(ε₀ Dielektrizitätskonstante des Vakuums), wobei über doppelt auftretende Indizes zu summieren ist. (Derartige Ansätze wurden zuerst 1882 von W. Gibbs gemacht.) Der zweite Summand in (1) beschreibt die räumliche Dispersion. Die Berechnung des Gyrationstensors 3. Stufe g_ijk aus molekülphysikalischen Vorstellungen heraus gelang M. Born und G. W. Oseen 1915 im Rahmen der Gitteroptik. Bei fehlender Absorption gilt g_ijk= -g_jik mit reellen Tensorkomponenten.

Mit vorgegebenem Wellenzahlvektor k einer sich im Kristalle ausbreitenden Welle bzw. mit dem zugehörigen Normalenvektor n=k/|k| kann durch die Beziehung

der Gyrationsoder Rotationsvektor G mit den Komponenten G_i definiert werden. Dabei bezeichnen ω die Kreisfrequenz, c die Lichtgeschwindigkeit und e_ikl den vollständigen antisymmetrischen Einheitstensor 3. Stufe, der folgendermaßen definiert ist: Es gilt e_ikl = 1, wenn ikl eine gerade, e_ikl = -1, wenn ikl eine ungerade Permutation von 1 2 3 ist, und e_ikl=0, wenn zwei und mehr Indizes übereinstimmen. Dann wird aus (1)


(2)

Aus dem Gyrationsvektor werden die Gyration g=G_in_i und der Gyrationstensor zweiter Stufe g_ij abgeleitet, der die Beziehung G_i=g_ijn_j befriedigt. Zu dem Tensor g_ij gehört in Analogie zur Kristalloptik die Gyrationsfläche, die angibt, wie groß die reziproke Quadratwurzel aus |g| in Lichtausbreitungsrichtung ist.

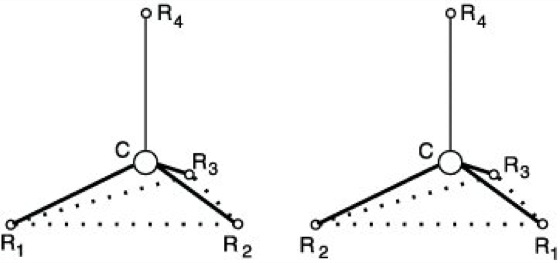
Manche Autoren bezeichnen als Gyrationsfläche auch die Fläche, die durch Abtragen der vorzeichenbehafteten Gyration g in Lichtausbreitungsrichtung entsteht. Ein Beispiel für einen einachsigen Kristall der Symmetrie

m ist in Abb. 2 zu sehen.

Bei einem isotropen Medium, wie z.B. NaClO₃ oder Flüssigkeiten, ist der Gyrationsvektor parallel zur Lichtausbreitungsrichtung gerichtet G_i = g_isn_i, und die Materialgleichung enthält nach (2) nur die beiden Parameter ε und g_is


(3)

Durch (3) wird ausgedrückt, daß eine bestimmte transversale Komponente von D auch durch die dazu senkrechte Transversalkomponente von E beeinflußt wird. Aus der Dispersionsbeziehung zwischen der Wellenzahl k und ω folgen die Brechungsindizes n(ω)_± für die beiden möglichen Wellen zu


(4)

Dabei bezieht sich n(ω) auf den Fall g_is=0. Das Verhältnis der beiden Transversalkomponenten von D ergibt sich zu ±i. Es entstehen also eine rechts zirkular und eine links zirkular polarisierte Welle. Für anisotrope Kristalle wird (4) komplizierter.

Die o. A. kann so verstanden werden, daß eine linear polarisierte Welle in der Substanz in zwei entgegengesetzt zirkular polarisierte Wellen gleicher Intensität zerlegt wird, die sich mit unterschiedlichen, durch n_± festgelegten Geschwindigkeiten ausbreiten. Beim Austritt aus der Substanz setzen sich beide Wellen wieder zu einer linear polarisierten Welle zusammen, allerdings mit gedrehter Polarisationsebene.

Bringt man zur Messung zwischen einen Polarisator und einen dazu senkrecht eingestellten Analysator die optisch aktive Substanz, so wird das Gesichtsfeld aufgehellt. Muß man bei einer Beobachtungsrichtung entgegen der Lichtrichtung den Analysator zur Herstellung von Lichtauslöschung aus diesem aufgehellten Zustande nach rechts (links) drehen, so liegen Rechts(dextrogyre, r,+)- oder Links(lävogyre, l,-)-Substanzen vor.

Bei Kristallen wird als spezifische Drehung (α) der Drehwinkel α je mm durchlaufene Kristalldicke definiert. Einige Werte sind in der Tabelle zu finden. Bei reinen Flüssigkeiten wird die spezifische Drehung [α] auf 100 mm Schichtdicke, bei aktiven Lösungen auf 1 g Substanz in 100 ml Lösung und ebenfalls 100 mm Schichtdicke bezogen. Die spezifische Drehung ist also [α]=100 α/(lc) mit α als Drehungswinkel bei einer Schichtdicke l in dm und einer Konzentration c in g/100 ml. Die spezifische Drehung ist im allgemeinen unabhängig von der Konzentration (Biotsches Gesetz), falls keine chemische Reaktion zwischen Lösungsmittel und aktiver Substanz stattfindet.

Das molekulare Drehvermögen (Molekularrotation) ist durch [m]=[α]·Molekulargewicht/100 definiert. Für Rohrzucker ist [α]=66,5°.

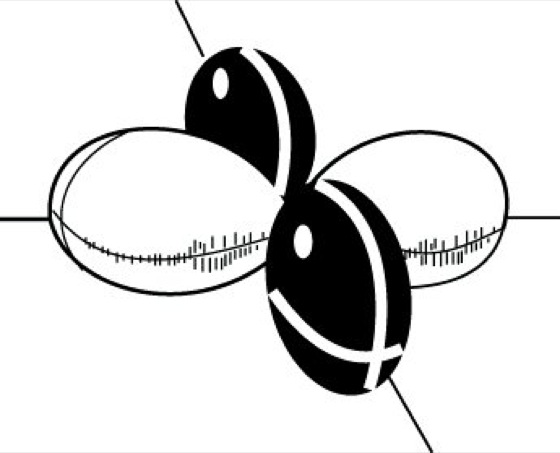
Im Inneren eines nicht absorbierenden optisch aktiven Kristalles breiten sich im allgemeinen parallel zu einer gegebenen Wellennormalenrichtung n zwei entgegengesetzt elliptisch polarisierte Wellen (privilegierte Schwingungen) mit zwei entsprechenden unterschiedlichen Brechungsindizes aus (Abb. 3). Die großen Achsen der Schwingungsellipsen liegen parallel zu den Schwingungsrichtungen des D-Vektors, die zur Richtung n bei verschwindender Gyration gehören würden. Ist n parallel zu einer Binormalen (Kristalloptik) gerichtet, so entstehen zwei zueinander entgegengesetzt zirkular polarisierte Wellen mit unterschiedlichen Brechungsindizes n₊ und n_- (zirkulare Doppelbrechung). Es ergibt sich (α)=-180°|n₊-n_-|/λ₀ grad mm^-1 mit λ₀ als Vakuumwellenlänge. Sind die beiden Grundmoden, die sich in einem Kristalle mit unterschiedlichen Brechungsindizes ausbreiten, nicht zirkular, sondern elliptisch polarisiert, so spricht man von elliptischer Doppelbrechung.

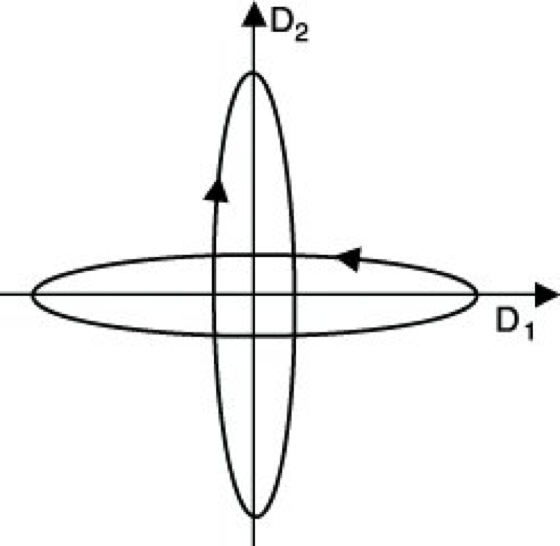
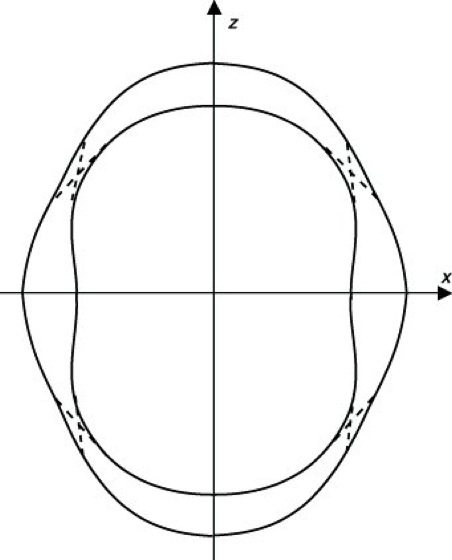
Die Normalen- und die Strahlenfläche (Kristalloptik) bestehen bei optisch aktiven Kristallen aus zwei nicht miteinander verbundenen Flächen (Abb. 4). Kristallpaare, die in ihrer Struktur bis auf Spiegelung identisch sind, werden optische Antipoden (optische Modifikationen) genannt; sie sind beide entgegengesetzt optisch aktiv. Ein Beispiel sind die beiden Modifikationen des Quarzes, Rechts- und Linksquarz. Flüssige Kristalle zeigen eine starke o. A. (Schadt-Helfrich-Effekt).

Das Drehvermögen ist wellenlängen- und temperaturabhängig. Die spezifische Drehung wird meist für 20°C und Natrium-D-Licht (Wellenlänge 589,3 nm) angegeben, ausgedrückt durch α^D₂₀. Für Quarz ist α^D₂₀=21,724 grad mm^-1. Weitere Werte finden sich in der Tabelle.

Die Wellenlängenabhängigkeit des Drehvermögens wird als Rotationsdispersion bezeichnet. Sie läßt sich außerhalb der Absorptionskante in guter Näherung durch die Biotsche Formel α=A/λ²+ B/λ⁴+C/λ⁶ beschreiben, wobei in vielen Fällen das erste Glied schon ausreichend ist. A, B und C sind Konstanten. Die Drehung ist für kurzwelliges Licht größer als für langwelliges (normale Rotationsdispersion, Tab.). Dagegen spricht man von anomaler Rotationsdispersion, wenn die Drehung mit zunehmender Wellenlänge anwächst. Das ist in der Nähe der Absorptionskante der Fall. In Verbindung mit Rotationsdispersion kann unterschiedliche Absorption der rechts und der links zirkular polarisierten Welle auftreten (Rotationsdichroismus, zirkularer Dichroismus). Insbesondere bei Lösungen findet man unterschiedliche Farberscheinungen, je nachdem, ob bei Weißlichtbeleuchtung rechts oder links zirkular polarisiertes Licht betrachtet wird. Eine Folge der Absorption in optisch aktiven Medien ist u.a. die Umwandlung von linear polarisiertem Licht in elliptisch polarisiertes.

Frisch zubereitete Lösungen ändern die Drehung im Laufe der Zeit in Richtung auf einen Endwert (Multirotation, Mutarotation).

Experimentell wird die Drehung durch Polarimeter, in der Zuckerindustrie durch Saccharimeter bestimmt. Anwendungen findet die Bestimmung der o. A. in der Zuckerindustrie, die der Rotationsdispersion in organischer Chemie und Biochemie.

Optische Aktivität 1: Die beiden optisch isomeren Formen eines optisch aktiven Moleküls.

Optische Aktivität 2: Gyrationsfläche eines einachsigen Kristalles mit der Symmetrie

m. Die weißen Flächen entsprechen positiver, die schwarzen negativer Gyration.

Optische Aktivität 3: Polarisationsellipsen der beiden Wellenausbreitungsmoden bei Doppelbrechung und gleichzeitiger optischer Aktivität. D₁, D₂ dielektrische Verschiebung.

Optische Aktivität 4: Schnitt durch die Normalenfläche eines zweiachsigen optisch aktiven Kristalles. Die punktierten Verbindungen ergeben die Normalenfläche eines nicht aktiven Kristalles.