Phasenkontrastverfahren, ein optisches Verfahren, mit dem die unsichtbaren, geringen Phasenänderungen, die das Licht in oder an mikroskopischen oder makroskopischen Objekten erleidet, in Intensitätsänderungen umgewandelt und damit sichtbar gemacht werden. Dies wird dadurch erreicht, daß bei der Abbildung dieser Objekte das ungebeugte (direkte Licht) gegenüber dem am Objekt gebeugten in der Phase und Amplitude verändert wird durch Eingriffe in das Beugungsspektrum des Objektes in der Pupillenebene. Ausgehend von der in der Mikroskopie in der Regel angewandten Köhlerschen Beleuchtungsanordnung verwendet man zunächst als Aperturblende eine kleine Zentralblende 1, auf die die Lichtquelle abgebildet wird (Abb. 1). Die von jedem Punkte dieser Blende ausgehenden Strahlen durchsetzen als Parallellichtbündel die Objektebene 3. Ein solches Bündel entspricht einer ebenen Welle. Ist in der Objektebene kein Objekt vorhanden, wird das gesamte von der Blende 1 ausgehende Licht in der Objektivbrennebene 6 vereinigt. Von dort aus verteilt es sich gleichmäßig über den ausgeleuchteten Teil der Zwischenbildebene 8. Ein in der Objektebene befindliches Objekt 4 lenkt einen Teil des Lichtes 9 durch Beugung aus seiner Richtung ab. In der Zwischenbildebene entsteht durch Interferenz zwischen direktem (10) und gebeugtem (9) Licht das Bild 4' des Objektes 4. Jedes normale Hellfeldobjektiv hat die Aufgabe, die durch das Objekt hervorgerufenen Amplituden- und Phasenbeziehungen in der Zwischenbildebene zu reproduzieren.

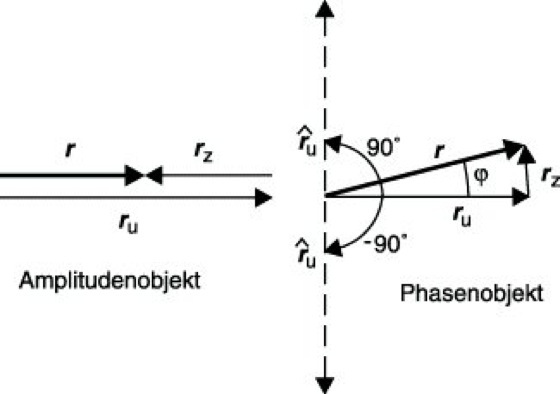
Wir betrachten nun die Wirkung eines Amplituden- und Phasenobjektes etwas genauer (Abb. 2). Wir beschreiben den Einfluß des Objektes auf das hindurchgehende Licht dadurch, daß wir zu dem (die komplexe Amplitude repräsentierenden) Vektor r_u des einfallenden und ungestört hindurchgegangenen Lichtes einen Zusatzvektor r_z addieren, der dem gebeugten Licht entspricht. Bei einem Amplitudenobjekt sind r_z und r_u einander entgegengerichtet, so daß die Länge des resultierenden Vektors r kleiner ist als die von r_u; das Objekt erscheint damit dunkler gegenüber seiner Umgebung. Ein reines Phasenobjekt dagegen dreht den Vektor r_u um einen kleinen Winkel ϕ, ohne jedoch seine (für die Intensität maßgebliche) Länge zu verändern. Der Zusatzvektor r_z steht daher näherungsweise senkrecht auf r_u. Der Winkel ϕ ergibt sich dabei aus der Dicke d des Objektes, der Brechzahldifferenz Δn zur Umgebung und der Wellenlänge λ zu ϕ=360°dΔn/λ.

Das Grundprinzip des P. besteht nun darin, daß man mit Hilfe eines in der Objektivbrennebene angebrachten Phasenplättchens, dessen Größe dem Bild der Aperturblende entspricht, die Phase des direkten (ungebeugten) Lichtes um ±90° ändert. Im Diagramm der Abb. 2 bedeutet das eine Drehung des Vektors r_u um ±90°. Gilt das Minuszeichen – das Phasenplättchen ist dann niedriger brechend als seine Umgebung –, so sind der gedrehte Vektor

und r_z antiparallel und die Situation ist die gleiche wie bei einem Amplitudenobjekt. Das Phasenobjekt, dessen Brechzahl größer als die seiner Umgebung ist, erscheint daher dunkel auf hellem Grunde (positiver Phasenkontrast). Gilt das Pluszeichen – das Phasenplättchen ist dann höher brechend als seine Umgebung –, so sind

und r_z parallel, und damit vergrößert sich die Länge des resultierenden Vektors im Vergleich zu der von r_u. Das Phasenobjekt erscheint somit hell auf dunklem Grunde (negativer Phasenkontrast). Wird durch das Phasenplättchen nur das direkte Licht beeinflußt, so spricht man vom strengen P. Werden infolge der endlichen Größe des Bildes der Aperturblende und damit durch das in seiner Ausdehnung notwendig größere Phasenplättchen in der Objektivbrennebene auch Anteile des gebeugten Lichtes beeinflußt, wird das P. als nichtstreng bezeichnet.

Der Bildkontrast wird größer, wenn man das direkte Licht nicht nur in der Phase verändert, sondern auch noch in der Intensität schwächt. Das Phasenplättchen wird deshalb noch mit einer absorbierenden Schicht versehen. Blendet man das direkte Licht in der Objektivbrennebene vollständig aus, so hat man eine Dunkelfeldanordnung (zentrales Dunkelfeld). Im Unterschied zur Dunkelfeldmikroskopie gelangt auch das direkte Licht ins Objektiv und wird erst in der Objektivbrennebene zurückgehalten. Ist das verwendete Licht nicht monochromatisch, dann sind auch bei farblosen Objekten und farblosem Einbettungsmittel Farbkontraste im Phasenkontrastbild möglich (farbiger Phasenkontrast).

Das P. kann sowohl im Durchlicht als auch im Auflicht angewandt werden. Es eignet sich am besten für Strukturen, die die Phase nur wenig ändern. Zum Messen wird es selten benutzt, da die beobachtete Intensität nur für einen kleinen Bereich der Phasenverschiebung (um 0°) der letzteren proportional ist.

Der Wunsch nach erhöhter Lichtstärke im Bilde erzwingt die Verwendung größerer Aperturblenden und damit ein Abgehen von den Forderungen des strengen P. Im Phasenkontrastbild treten dann helle Höfe um die Objekte auf (Haloeffekt) sowie Scheinstrukturen. Außerdem werden oft zu kleine Abmessungen der Objekte vorgetäuscht. Diese Effekte werden beobachtet, sobald die Breite des Phasenplättchens den Wert 0,2 λ/sinα überschreitet, wobei sinα die Apertur des Phasenplättchens bezeichnet.

Technische Durchführung und Anwendungen. Das P. wurde von F. Zernike (geb. 1888, Nobelpreis 1953) im Jahre 1932 ursprünglich zum Prüfen von Hohlspiegeln und Beugungsgittern entwickelt, jedoch bald darauf von ihm auf das Mikroskop übertragen. Hier fand es seine größte Verbreitung. Beim Phasenkontrastmikroskop wird im Durchlicht ein Phasenkontrastkondensor, im Auflicht ein Vertikal-Phasenkontrastilluminator benutzt. Diese besitzen meist eine Revolverscheibe mit zentrierbaren Ringblenden verschiedenen Durchmessers, die wahlweise eingeschaltet werden können. In der hinteren Brennebene der Phasenkontrastobjektive befinden sich die phasenverschiebenden und absorbierenden Elemente (Phasenplatte). Meistens ist die phasenändernde Schicht ringförmig (Phasenring). Phasenstreifen sind selten, da sie nicht frei von Azimutaleffekten sind. Sie erfordern Kondensorblenden in Spaltform. Die Phasenkontrastobjektive sind durch die Buchstaben Ph oder ähnlich gekennzeichnet; gelegentlich werden auch Phasenverschiebung und Absorption angegeben.

Die Anwendungen der Phasenkontrastmikroskopie sind sehr zahlreich. Im Durchlicht hat sie vor allem für die Zytologie und Bakteriologie Bedeutung gewonnen, weil man mit ihrer Hilfe ungefärbtes, im besonderen auch lebendes Material kontrastreich darstellen kann. In neuerer Zeit wird häufig die Refraktometrie lebender Zellen durchgeführt, weil deren Brechungsindex ihrer Trockenmasse proportional ist. Makroskopische P. werden zum Prüfen der Politur und Schlierenfreiheit hochwertiger Optik und von Beugungsgittern sowie zur Refraktometrie von Gasen und Flüssigkeiten verwendet. Mit dem P. wird dabei die Gleichheit der Brechzahlen beim Immersionsverfahren (Brechzahlbestimmung 4)) festgestellt.

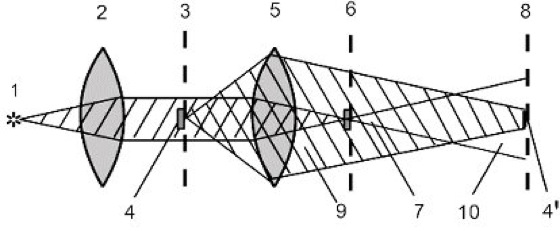
Phasenkontrastverfahren 1: Strahlengang im Phasenkontrastmikroskop. 1 Zentralblende, 2 Kondensor, 3 Objektebene, 4 Phasenobjekt, 4' Bild des Phasenobjektes, 5 Objektiv, 6 Objektivbrennebene, 7 Prismenplättchen, 8 Zwischenbildebene, 9 gebeugtes Licht, 10 direktes Licht.

Phasenkontrastverfahren 2: Prinzip des Phasenkontrastverfahrens. Erläuterung im Text.