rasteroptische Erscheinungen, optische Erscheinungen, die bei Durchstrahlung von zwei aufeinandergelegten Rastern mit einem parallelen Lichtbündel zu beobachten sind. Von besonderem Interesse sind die Moiré-Erscheinungen, die dann auftreten, wenn sich die beiden Raster nur wenig unterscheiden. Im einfachsten Falle bestehen die Raster aus äquidistanten geradlinigen hellen und dunklen Streifen. Kombiniert man zwei derartige Raster, die einen ein wenig verschiedenen Streifenabstand (Rasterperiode) besitzen, so miteinander, daß die Rasterlinien zueinander parallel sind, so beobachtet man als Moiré-Bild (kurz Moiré genannt) ein neues Raster mit einer stark vergrößerten Periode. Dieser Effekt läßt sich mathematisch am einfachsten beschreiben, wenn man annimmt, daß die Transparenzverteilungen der beiden Raster von der Form T₁∝1+cos(2πx/p₁) bzw. T₂∝1+cos(2πx/p₂) sind, wobei p₁ und p₂ die Rasterperioden bezeichnen. Die Gesamttransparenz T ist dann durch das Produkt der Einzeltransparenzen T₁ und T₂ gegeben. Unter Verwendung des Additionstheorems cosαcosβ = 1/2[cos(α+β) + cos(α-β)] ergibt sich so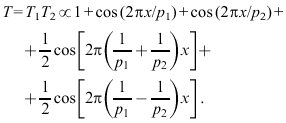


.

Durch optische Filterung, z.B. unscharfe Abbildung, werden die Anteile mit den hohen Ortsfrequenzen unterdrückt, so daß schließlich ein niederfrequentes Moiré-Bild mit dem Intensitätsverlauf

entsteht. Dessen Periode ist um so größer, je weniger sich die Einzelperioden p₁ und p₂ voneinander unterscheiden.

Ebenfalls ein Moiré-Muster in Gestalt abwechselnd heller und dunkler Streifen ergibt sich, wenn zwei identische Raster um einen kleinen Winkel Θ gegeneinander verdreht werden. Die Moiré-Streifen stehen dann senkrecht zu der Winkelhalbierenden der Rasterlinien (Abb. 1). Die Mitten der hellen Moiré-Streifen gehen durch die Schnittpunkte der Mitten der dunklen Rasterstreifen. Der Abstand der Moiré-Streifen beträgt


,

wobei p die Rasterperiode bezeichnet. Verschiebt man eines der Raster um eine Periode, so verschiebt sich das Moiré-Bild um S. Wenn sich das eine Raster mit der Geschwindigkeit v_R bewegt, verschiebt sich daher das Moiré-Muster mit der Geschwindigkeit


.

Moiré-Bilder entstehen auch unter allgemeineren Bedingungen. Z.B. können aus konzentrischen Kreisen bestehende Raster oder verformte Streifenraster (s.u.) verwendet werden. Die Lage der auftretenden Moiré-Kurven ist stets dadurch bestimmt, daß (wie im obigen Falle zweier gegeneinander verdrehter Raster) die Mitten der hellen Moiré-Kurven durch die Schnittpunkte der Mitten der dunklen Rasterkurven hindurchgehen.

Anwendung finden die r. E. in Entfernungsmessern und Wegmeßsystemen sowie bei der Messung von topographischen Abweichungen und Deformationen. Zur Wegmessung lassen sich zwei gleichartige Raster verwenden, wobei ein kurzes Raster an einem langen Rastermaßstabe vorbeigeführt wird. Durch optoelektronische Abtastung der Moiré-Erscheinungen im Durchlicht oder Auflicht läßt sich eine Vorwärts/Rückwärts-Zählung in Bruchteilen der Rasterperiode p vornehmen. Durch Interpolation gelangt man in den Submikrometerbereich. Auch zur Vermessung der Topographie von Körperoberflächen lassen sich Raster nutzen. Durch schräge parallele Beleuchtung unter dem Einfallswinkel ϕ wird das Schattenbild eines Rasters auf die Oberfläche z(x,y) projiziert und durch das Raster hindurch unter dem Winkel Ψ zur Flächennormale beobachtet (Abb. 2). Das Raster befindet sich dabei in unmittelbarer Nähe der Oberfläche. Man sieht ein Höhenlinienbild der Oberfläche, wobei sich die Höhe von einer Höhenlinie zur benachbarten um z=p/(tanϕ+tanΨ) ändert.

Die Empfindlichkeit der Messung läßt sich in weiten Grenzen durch die Wahl von p, ϕ und Ψ variieren. Zur Messung von Deformationen werden Raster auf die Oberfläche aufgeklebt und z.B. symmetrisch mit zwei kohärenten Bündeln unter einem Winkel ±ϕ beleuchtet, wobei ϕ mit dem Winkel übereinstimmt, unter dem die erste Beugungsordnung (bezüglich des Rasters) auftritt (Abb. 3). Bei Beobachtung senkrecht zum Raster überlagern sich zwei Wellen, die die Rasterdeformationen als Wellenfrontdeformationen wiedergeben. Sie erzeugen ein Interferenzbild, aus dem auf die Deformation geschlossen werden kann.

Eine andere, öfters verwendete Methode zur Bestimmung der Deformation von festen Körpern ist die folgende. Man stellt zunächst ein zweidimensionales durchsichtiges Modell des Körpers her und bringt darauf ein Raster in Gestalt äquidistanter geradliniger Streifen an. Unter dem Einfluß äußerer Kräfte verformt sich das Modell und mit ihm das Raster. Auf das deformierte Modell wird nun eine durchsichtige Platte mit dem ursprünglichen (nicht verformten) Raster gelegt und die Moiré-Erscheinung beobachtet. Die dabei auftretenden hellen Moiré-Kurven sind die geometrischen Orte aller Punkte, die in der zu den ursprünglichen Rasterstreifen senkrechten Richtung die gleiche Verschiebung erfahren haben. Der Wert der genannten Verschiebung ändert sich dabei von einer Moiré-Kurve zur nächsten um den Streifenabstand des ursprünglichen Rasters. Auf diese Weise lassen sich, wenn man bei der Herstellung des Moiré-Bildes die Streifen des ursprünglichen Rasters einmal in x- und einmal in y-Richtung orientiert, die Verschiebungen vollständig bestimmen. Die Verzerrungen (Elemente des Verzerrungstensors) ergeben sich aus den Verschiebungen durch partielle Differentiation nach x und y. Diese partiellen Ableitungen können aus den genannten Moiré-Bildern z.B. durch graphische Differentiation ermittelt werden. Auf direktem Wege lassen sie sich dadurch bestimmen, daß man entweder das Moiré-Bild zweier identischer, gegeneinander verschobener photographischer Kopien des deformierten Rasters erzeugt oder indem man ein Moiré-Bild zweiter Ordnung ("Moiré des Moiré") herstellt. Letzteres geschieht, indem man zwei photographische Kopien des bei der Kombination des ursprünglichen Rasters mit dem deformierten Raster auftretenden Moiré-Bildes (Moiré 1. Ordnung) gegeneinander verschoben aufeinanderlegt.

Die einzelnen Moiré-Techniken werden verschiedentlich unter dem Begriff Moiré-Interferometrie zusammengefaßt. Moiré-Erscheinungen werden in der Dupligrammetrie auch zur Auswertung von Interferogrammen genutzt.

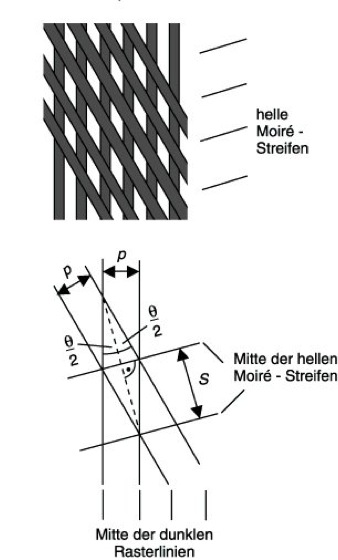
Rasteroptische Erscheinungen 1: Moiré-Streifen an zwei gegeneinander verdrehten Rastern.

Rasteroptische Erscheinungen 2: Rastertopographie. Durch schräge Beleuchtung wird ein Schattenbild eines Rasters auf die Objektfläche projiziert, welches bei der Beobachtung durch das Raster ein topographisches Streifenbild erzeugt.

Rasteroptische Erscheinungen 3: Rasteroptische Methode zum Nachweis von Deformationen.