Spannungsoptik, Wissenschaftsgebiet zur Untersuchung von Spannungen und Verformungen von beanspruchten Bauteilen durch Messung der Spannungsdoppelbrechung an Modellen (die Ergebnisse werden mit Ähnlichkeitsgesetzen auf die Originalbauteile übertragen) oder in spannungsoptisch empfindlichen Schichten, die auf das Originalbauteil aufgebracht werden, oder an durchsichtigen Originalteilen (Polymere, Glas) zur Qualitätssicherung. Die theoretischen Grundlagen der S. sind die Gesetze der Kristalloptik und der Mechanik. Die Beanspruchung erzeugt im vorher optisch isotropen Körper eine optische Anisotropie, die mit einem Polariskop gemessen wird und mit dem Indexellipsoid beschrieben werden kann. Dessen Hauptbrechungsindizes n₁, n₂ und n₃ stehen mit den drei Hauptnormalspannungen σ₁, σ₂ und σ₃, in einem Punkte in folgendem Zusammenhang (Maxwell-Ansatz)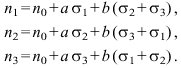

Dabei ist n₀ der Brechungsindex des Materials im Ausgangszustand, a und b sind Materialkonstanten, die von der Wellenlänge des Lichtes abhängig sein können. Ersetzt man in den obigen Gleichungen die Spannungen σ durch die Hauptdehnungen ε, so gelangt man zu dem Neumann-Ansatzn₁=n₀+a'ε₁+b'(ε₂+ε₃) usw. (a'≠a, b'≠b). Am einfachsten lassen sich "ebene Modelle" (Scheiben, die in ihrer Ebene belastet sind) untersuchen. Sie weisen einen "ebenen" Spannungszustand auf: σ₁ und σ₂ sind über die Scheibendicke d konstant, die senkrecht zur Scheibenebene gerichtete Hauptnormalspannung σ₃ ist gleich 0. Dann wird bei senkrechter Durchstrahlung der Scheibe mit parallelem, polarisiertem Licht der optische Gangunterschied s der in den Hauptspannungsrichtungen schwingenden Teilstrahlen s = d(n₁-n₂) = d(a-b)(σ₁-σ₂) bzw. der auf die Wellenlänge λ bezogene relative Gangunterschied m mit Kλ=(a-b)/λ:

Dies ist die Grund- oder Hauptgleichung der S.

Eine Messung von m, der Isochromatenordnung, liefert die Differenz der Hauptnormalspannungen, die doppelt so groß wie die festigkeitsrelevante maximale Schubspannung τ_max ist. Die wellenlängenabhängige Materialkonstante Kλ wird spannungsoptische Konstante genannt. In der Glas- und Polymerforschung, wo die innere Struktur der Werkstoffe die größere Rolle spielt, werden dagegen die Konstanten a und b als photoelastische Konstanten, ihre Differenz (a-b) als spannungsoptische Konstante bezeichnet. Die Maßeinheit ist hier das Brewster (1 Brewster = 1 TPa^-1). In der Technik versteht man unter der spannungsoptischen Konstanten meist die Größe fσ=1/Kλ (Einheit N/Ordnung·mm).

Die Messung der Spannungsdoppelbrechung erfolgt in einer spannungsoptischen Apparatur, einer hochwertigen Ausführung des Spannungsprüfers. In diesem Polariskop wird zunächst Licht mit definierter Polarisation (linear oder zirkular) erzeugt. Nach Durchstrahlung des Modells wird der veränderte, im allgemeinen elliptische Polarisationszustand analysiert (Ellipsometrie).

Durchstrahlt man das Modell mit linear polarisiertem Licht, so ergibt sich die Intensität I des aus dem Analysator austretenden Lichtes bei gekreuzter Stellung der Polarisationsfilter (Dunkelfeld) zu

Dabei ist I₀ die primäre auf das Modell fallende Intensität und α der Winkel zwischen der durch die Polarisatorstellung bestimmten Schwingungsrichtung des elektrischen Feldstärkevektors und einer Hauptnormalspannungsrichtung im Modell. Im monochromatischen Licht ergeben sich dunkle Linien für m=0, 1, 2, ... Sie heißen Isochromaten oder Isochromen und kennzeichnen Orte gleicher maximaler Schubspannung. Im weißen Licht sind sie farbige Linien, da jeweils eine bestimmte spektrale Komponente des Lichtes durch Interferenz ausgelöscht wird. Die Isochromate 0. Ordnung ist dabei immer schwarz.

Schwarze Linien entstehen nach obiger Formel auch, wenn α=0 oder π/2 ist, d.h., wenn die Schwingungsrichtung des linear polarisierten Lichtes mit einer Hauptnormalspannungsrichtung im Modell übereinstimmt. Diese Linien heißen Isoklinen (Richtungsgleichen). Sie markieren Modellpunkte mit gleicher Hauptspannungsrichtung. Bei Drehung des Polarisationskreuzes wandern die Isoklinen über das Modell, während die Isochromaten ihre Lage nur mit der Größe der Belastung ändern. Aus einer Schar von Isoklinen läßt sich das Netz der Hauptnormalspannungslinien ermitteln.

Eine Beobachtung der Isochromaten allein, ohne Störung durch die Isoklinen, kann im zirkular polarisierten Licht erfolgen. Für die Intensität der austretenden Strahlung gilt dann I=I₀sin²mπ im Dunkelfeld, im Hellfeld, d.h. bei Parallelstellung von Polarisator und Analysator, gilt I=I₀cos²mπ. Im Dunkelfeld beobachtet man demnach Isochromaten ganzzahliger Ordnung (m=0, 1, 2, ...), im Hellfeld halbzahliger Ordnung (m=1/2, 3/2, 5/2, ...). Dazwischen liegende Ordnungen lassen sich durch Verwendung eines Kompensators sichtbar machen. Beispiele für Isochromaten und Isoklinen zeigen Abb. 1 und 2.

Aus den gemessenen Werten der Isochromatenordnung und den Isoklinen können die Hauptnormalspannungen σ₁ und σ₂ auch einzeln entweder numerisch oder mit zusätzlichen Meßverfahren ermittelt werden. Vielfach geben auch schon die Isochromaten als Linien konstanter Hauptschubspannung Aufschluß über die Beanspruchung. Abb. 3 zeigt ein Beispiel aus der Materialforschung.

Zur Untersuchung räumlicher Spannungszustände wird meist das Einfrierverfahren eingesetzt. Streulichtverfahren und integrale Spannungsoptik dienen überwiegend zur Qualitätsüberwachung in der Polymer- und Glasproduktion. Für direkte Messung an Originalbauteilen ist das Oberflächenschichtverfahren sehr gut geeignet (s. Farbtafel ). Die S. läßt sich auch in Verbindung mit kurzzeitphotographischen und elektronischen Hilfsmitteln zur Untersuchung zeitlich veränderlicher Vorgänge (z.B. Schwingungen, Bruchvorgänge, Ausbreitung von Stoßwellen) einsetzen (Abb. 4).

Die Photoplastizität und die Photoviskoelastizität befassen sich speziell mit plastischen Verformungen und Kriecherscheinungen.

Die Modellwerkstoffe sind heute überwiegend Epoxidharze, Polyesterharze und Polycarbonate; für das Einfrierverfahren fast ausschließlich Epoxidharze. Teilweise neigen sie jedoch zur Ausbildung des Nulleffekts.

Geschichtliches. Die Spannungsdoppelbrechung wurde 1816 von D. Brewster an Gläsern entdeckt. Er erkannte auch schon ihre Bedeutung für die Praxis. Die physikalische Interpretation wurde um 1845 durch F. Neumann (Dehnungsansatz) und 8 Jahre später von J. C. Maxwell (Spannungsansatz) gegeben. Anwendungen sind seit etwa 1900 bekannt, vor allem durch A. Mesnager; er arbeitete überwiegend mit Modellen aus Glas und erfand das Oberflächenschichtverfahren.

Mit der Entdeckung geeigneter Kunststoffe setzte um 1910 durch E. G. Coker eine rasche Entwicklung der ebenen S. ein. Wesentliche Beiträge stammen von M. M. Frocht, L. Föppl und E. Mönch. Das Einfrierverfahren zur Untersuchung räumlicher Spannungsverteilungen wurde 1936 durch G. Oppel begründet.

Spannungsoptik 1: Isochromaten in einem mittig belasteten Balkenträger, aufgenommen mit Natriumlicht im zirkularen Hellfeld.

Spannungsoptik 2: Isochromaten und Isoklinen (gestrichelt nachgezeichnet) in einem mittig belasteten Balkenträger; linear polarisiertes weißes Licht.

Spannungsoptik 3: Isochromaten längs einer Glasfaser (Länge 3 mm, ∅ 80 μm) in einer Polycarbonatmatrix (Dicke 450 μm), aufgenommen mit einem Laserscanning-Mikroskop. Oben: Faser unzerstört, kurz vor dem Riß; unten: Faser im rechten Drittel gerissen.

Spannungsoptik 4: Stoßbelastete Scheibe mit Riß. Isochromatenaufnahmen mit einer Cranz-Schardin-Hochgeschwindigkeitskamera im monochromatischen Licht.