Speckle (engl., "Fleckchen"), Granulation, eine Vielstrahlinterferenzerscheinung, hervorgerufen von Wellen, die von vielen kohärenten aber stochastisch verteilten Lichtquellen herrühren. Die Phasenbeziehungen zwischen den Wellen sind dabei zufälliger Natur. Im allgemeinen ist die Erscheinung des S. ein störender Effekt, sie wird aber in der Meßtechnik vielfältig genutzt. Zur Erzeugung von Speckle-Bildern genügt die Beleuchtung einer streuenden Fläche im Auflicht oder Durchlicht (Abb. 1) mit dem Lichte eines Lasers. Das Speckle-Muster ist eine kontrastreiche Interferenzerscheinung. Dabei interferieren in einem jeden Punkte P der Auffangebene die Streuwellen, die von den verschiedenen Streuzentren ausgehen. Die Phase einer Streuwelle ist durch die Phase der Laserwelle an dem betreffenden Streuzentrum und dessen Abstand vom Aufpunkte P bestimmt. Wegen der großen räumlichen Kohärenz der Laserstrahlung ändert sich deren Phase zeitlich an allen Streuzentren um genau den gleichen Wert. Die für die Intensitätsverteilung im Speckle-Bild maßgeblichen Phasenbeziehungen zwischen den Streuwellen bleiben davon unberührt, so daß das Speckle-Muster zeitlich konstant ist. Wegen der zufälligen räumlichen Verteilung der Streuzentren hat auch das Speckle-Bild zufälligen Charakter. Bewegt man sich über die Auffangebene, so findet man für die Intensität am häufigsten den Wert Null. Die Streuung

der Intensität ist gleich dem Mittelwert

der Intensität über die Speckle-Verteilung. Die Feinheit der auftretenden Struktur, ausgedrückt durch die "Speckle-Korngröße" Δy, hängt von der zugelassenen Apertur sinφ und der Wellenlänge λ ab, und zwar gilt Δy=λ/(2sinΦ). Deshalb tritt S. bei der optischen Abbildung als Bildstörung auf. Das betrifft besonders die hohen Ortsfrequenzen. Als Vielstrahlinterferenzmuster kann das S. auch als statischer Informationsträger für verschiedenartige Meßverfahren dienen.

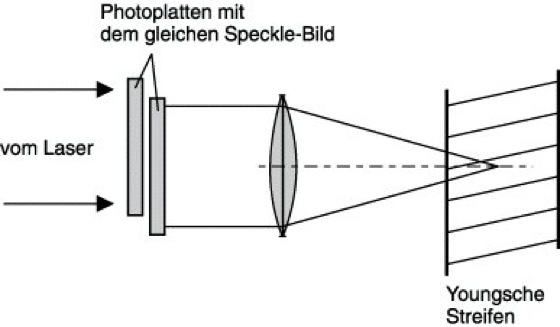
Speckle-Korrelationstechniken (Speckle-Photographie). Zwei gleiche, auf je einer Photoplatte aufgenommene, gegeneinander ein wenig verschobene Speckle-Bilder werden von Laserlicht durchstrahlt (Abb. 2). Mit einer Linse wird das räumliche Fourier-Spektrum (Beugungsbild) erzeugt. Dieses enthält Youngsche Interferenzstreifen, deren Abstand umgekehrt proportional zur Größe der Verschiebung ist und die senkrecht zu der Verschiebungsrichtung liegen. Die Zweiplattenmethode läßt sich auch in eine Doppelbelichtungstechnik umwandeln, wobei die Photoplatte zwischen der ersten und der zweiten Exposition verschoben wird. Die Youngschen Streifen zeigen an, daß die beiden Speckle-Bilder miteinander korreliert sind. Sie treten nicht auf, wenn keine Korrelationen bestehen. Auf diesem Umstande beruht die folgende Speckle-Korrelationstechnik: Eine nach der Doppelbelichtungstechnik hergestellte Aufnahme zweier etwas unterschiedlicher Speckle-Verteilungen (oder die entsprechende Kombination zweier Photoplatten) wird in einem optischen System auf eine Auffangebene abgebildet (Abb. 3). In der Fokalebene der Linse L₁ ist eine Doppelschlitzblende so angeordnet, daß die Mitten der Schlitze mit den Minima der beiden Youngschen Streifen der ersten Beugungsordnung zusammenfallen. Das mit der Linse L₂ erzeugte Bild ist dann von dunklen Streifen, den Korrelationsstreifen, durchzogen, welche die Stellen anzeigen, an denen die beiden Speckle-Muster miteinander korreliert sind.

Mit einer derartigen Korrelationstechnik lassen sich (z.B. durch mechanische Spannungen verursachte) Verrückungen in der ebenen Oberfläche eines Objektes nachweisen. Man verwendet dazu eine schräge Objektbeleuchtung aus zwei zur Oberflächennormale symmetrischen Richtungen (Abb. 4). In diesem Falle gehen von jedem Streuzentrum zwei Streuwellen aus, die von jeweils einer der zwei kohärenten Laserwellen erzeugt werden und daher miteinander interferieren. Verschiebt sich ein Oberflächenelement an der Stelle x in x-Richtung um eine kleine Strecke d_x, so ändert sich der Gangunterschied zwischen den genannten Streuwellen um 2 d_x sin Θ. Die Folge davon ist eine Intensitätsänderung an der betreffenden Stelle des Speckle-Bildes. (Die Verschiebung d_x ist so klein, daß die damit verbundene Verschiebung des Bildpunktes kleiner als die Speckle-Korngröße ist.) Bei einer Verschiebung des Oberflächenelementes um d_x=λ/(2 sinΘ) erreicht der Gangunterschied gerade den Wert λ; das bedeutet, die Intensität durchläuft dabei eine volle Periode. Wendet man daher die Speckle-Korrelationstechnik auf zwei Speckle-Bilder an, von denen eines vor und eines nach der Verformung aufgenommen wurde, so geben die auftretenden Korrelationsstreifen Auskunft über die stattgefundenen Verrückungen. Sie markieren Orte gleicher Verrückung (in x-Richtung), wobei sich der Wert der Verrückung von Streifen zu Streifen um λ/(2sinΘ) ändert. Bemerkenswert ist, daß eventuell zusätzlich erfolgende Verrückungen in den anderen beiden Koordinatenrichtungen keinen Einfluß auf die Messung haben.

Die durch die Verformung der Oberfläche verursachte Änderung des Speckle-Musters kann auch so gemessen werden, daß man die Photoplatte durch eine Detektormatrix ersetzt und die Speckle-Korngröße durch Abblenden größer macht als die empfindliche Fläche der Einzeldetektoren. Auf diese Weise können Verrückungen photoelektrisch ermittelt werden.

Die Speckle-Korrelationstechnik kann auch zur Subtraktion zweier Bildinhalte verwendet werden. Die Aufgabe besteht darin, zwei als Transparenzverteilungen (Dias) vorliegende Bilder, die sich nur an einzelnen Stellen unterscheiden, zu vergleichen und die Unterschiede aufzuzeigen. Man bringt zu diesem Zwecke die beiden Bilder nacheinander vor ein und dieselbe Photoplatte und photographiert ein Speckle-Bild, das z.B. bei Durchstrahlung einer Mattscheibe entsteht, durch das jeweilige Bild hindurch. Vor der zweiten Aufnahme verschiebt man die Photoplatte nur ein wenig. Die doppelbelichtete Photoplatte wird nun mit parallelem Lichte durchstrahlt und mit Hilfe eines Objektivs auf eine Auffangebene abgebildet. In der Fokalebene des Objektivs wird ein undurchsichtiger Schirm mit einem Spalte so angeordnet, daß dessen Mitte mit dem Minimum eines Youngschen Streifens zusammenfällt. In der Auffangebene wird dann die Differenz der beiden Bildinhalte sichtbar.

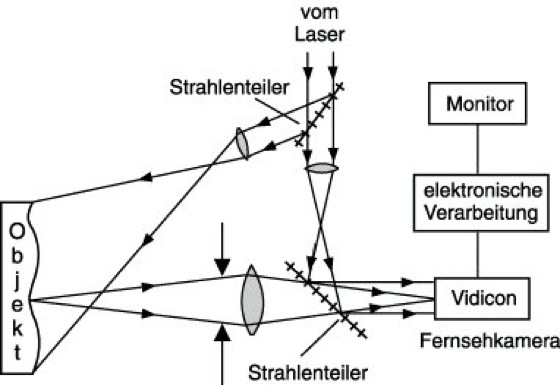
Speckle-Interferometrie. Dabei wird dem vom Objekt erzeugten stochastischen Felde ein deterministisches oder ein ebenfalls stochastisches Referenzwellenfeld überlagert. Es besteht eine starke Analogie zur Hologramminterferometrie. Technisch besonders bedeutsam ist die "elektronische Speckle-Interferometrie" (ESPI). Dabei wird mit einer hochauflösenden Fernsehkamera (Abb. 5) das Speckle-Feld des Objektes mit einer angepaßten Referenzwelle auf der Photokathode des Vidikons überlagert. Durch geeignete Wahl der Öffnungsblende wird das Speckle-Korn so groß gemacht, daß das S. örtlich aufgelöst werden kann. Das von der Kamera gelieferte elektrische Signal läßt sich speichern und mit Signalen von Folgezuständen subtraktiv oder multiplikativ überlagern. Auf diese Weise sind zeitgemittelte und Doppelexpositionsaufnahmen möglich. Von Vorteil ist das Fehlen chemischer Zwischenschritte. Nachteilig ist die begrenzte laterale und Tiefenauflösung.

Speckle-Astronomie. Die durch die Turbulenz der Atmosphäre verursachte Szintillation der Sterne begrenzt die bei konventionellen photographischen Aufnahmen mit langer Belichtung erreichbare Winkelauflösung auf 1 Bogensekunde. Mit Hilfe der Speckle-Technik ist es möglich, den störenden Einfluß der Atmosphäre zu eliminieren und so zu einer deutlich höheren Auflösung stellarer Objekte zu gelangen, die lediglich durch die Beugung am Teleskop begrenzt wird. Man geht dazu folgendermaßen vor: Mit Hilfe eines Teleskopes werden unter Verwendung eines Bildverstärkers kurzzeitig viele Einzelaufnahmen des Objektes gemacht (etwa 100 Bilder pro Sekunde). Eine jede von ihnen zeigt ein Speckle-Bild des Objektes, das jedoch wegen des sich ändernden Zustandes der Atmosphäre von Aufnahme zu Aufnahme verschieden ist. Von den einzelnen Bildern wird jeweils die Fourier-Transformierte (Beugungsbild) erzeugt und photographiert. Dann wird über viele (etwa 1000) derartige Aufnahmen gemittelt. An diesem gemittelten Beugungsbild wird erneut eine Fourier-Transformation vorgenommen. Dadurch erhält man das Ensemble-Mittel der Autokorrelationsfunktion für die Intensität im beugungsbegrenzten Bilde des Objektes. Insbesondere bei der Beobachtung von Doppelsternen läßt sich so eine erhebliche Steigerung der Auflösung erreichen (um einen Faktor 30 bis 50 je nach Teleskop).

Rauhigkeitsmessungen. Das Speckle-Muster ist auch von der Rauhtiefe einer Oberfläche abhängig. Rauhigkeitsmessungen können so ausgeführt werden, daß man mit Hilfe der Doppelbelichtungstechnik zwei Speckle-Bilder der Oberfläche photographiert, wobei die zweite Aufnahme entweder bei geänderter Richtung oder bei veränderter Wellenlänge des zur Beleuchtung dienenden Laserlichtes erfolgt. Nach dem in Abb. 2 dargestellten Verfahren werden dann Youngsche Streifen erzeugt, aus deren Kontrast auf die Rauhtiefe geschlossen werden kann.

Speckle 1: Entstehung von Speckle durch Vielstrahlinterferenzen. P Punkt der Auffangebene (Auffangpunkt).

Speckle 2: Youngsche Streifen als Ergebnis der Überlagerung gleichartiger, aber verschobener Speckle-Bilder.

Speckle 3: Speckle-Korrelationstechnik. Ph Photoplatte mit 2 Speckle-Bildern; L₁, L₂ Linsen, B Blende, A Auffangebene.

Speckle 4: Anordnung zum Nachweis von "in-plane"-Bewegungen eines Objektes.

Speckle 5: Elektronische Speckle-Interferometrie (ESPI).