Sterninterferometer, Gerät zur interferometrischen Bestimmung des Winkeldurchmessers von Sternen. Die verfügbaren Teleskope vermögen Fixsterne räumlich nicht aufzulösen. Das Sternlicht erzeugt nämlich in der Brennebene des Teleskops ein Beugungsscheibchen, dessen Gestalt durch die Apertur des Teleskops bestimmt wird, mit der tatsächlichen Ausdehnung des Sterns jedoch nichts zu tun hat. Hier erzielte A.A. Michelson einen bedeutenden Fortschritt durch Anwendung einer interferometrischen Methode.

Das S. nach Michelson. Bei diesem Gerät (Abb.) fällt das Sternlicht auf zwei in einem Abstand d angebrachte Spiegel S1 und S2, die es über zwei Umlenkspiegel S3 und S4 in ein Teleskop schicken, in dessen Brennebene es fokussiert wird. Zusätzlich in den Strahlengang gebracht sind Filter, die dafür sorgen, daß die Beobachtung bei einer bestimmten Wellenlänge erfolgt. Die von irgendeinem kleinen Bereich der Sternoberfläche kommenden, auf S1 und S2 fallenden Lichtstrahlen, die wegen der großen Entfernung des Sternes als parallel angesehen werden können, erzeugen in der Brennebene des Teleskops eine Interferenzfigur in Gestalt geradliniger, äquidistanter Streifen. Sie ist dadurch bedingt, daß die beiden Spiegel nicht genau unter 45° gegen die Teleskopachse geneigt sind (Interferenzen gleicher Dicke). Das von einem anderen Bereich der Sternoberfläche ausgesandte Licht, das unter einem geringfügig veränderten Winkel auf die Spiegel trifft, liefert wegen des auftretenden Gangunterschiedes dsinα≈dα, wobei α den Winkelunterschied bezeichnet (Abb.), ein gegenüber dem ersten verschobenes Interferenzmuster. Die bei der Beobachtung stattfindende Überlagerung der von allen Stellen der Sternoberfläche erzeugten Interferenzmuster ergibt dann ein mehr oder weniger verwaschenes Interferenzbild. Seine Sichtbarkeit ist offenbar dann drastisch vermindert, wenn der Gangunterschied zwischen zwei Strahlen, von denen der eine vom linken und der andere vom rechten Rande des Sternes ausgeht, in die Größenordnung der Wellenlänge λ des Lichtes gelangt (oder noch größer ist), d.h., wenn dα₀

λ gilt, wobei α₀ den gesuchten Winkeldurchmesser des Sternes bezeichnet. Damit kann man aus einer Messung der Sichtbarkeit des Interferenzbildes auf den Sterndurchmesser schließen. Zur genaueren Auswertung benutzt man die theoretische Kurve für die Sichtbarkeit, die sich nach dem van Cittert-Zernike-Theorem für den Fall leicht ausrechnen läßt, daß man den Stern durch eine gleichförmig leuchtende Kreisscheibe idealisiert. Das Ergebnis ist die in Abb. 2 zu Kohärenzintervall dargestellte Kurve, wobei für v die Größe α₀d/λ einzusetzen ist. diese Kurve erreicht für


(1)

zum ersten Male den Wert Null. Die Messung des Sterndurchmessers α₀ erfolgt nun in der Weise, daß man den Spiegelabstand d, beginnend mit kleinen Werten, so lange vergrößert, bis das Interferenzbild verschwindet. Der so erhaltene kritische Wert von d ist nichts anderes als das Kohärenzintervall für das (spektral gefilterte) Sternlicht. Setzt man ihn in (1) ein, so erhält man α₀. Nach diesem Verfahren wurden Sterndurchmeser bis herab zu etwa 0,02″ bestimmt.

Bei Spiegelabständen von vielen Metern machen sich jedoch zwei Schwierigkeiten bemerkbar. Erstens müssen wegen der endlichen Bandbreite Δλ der (gefilterten) Strahlung die beiden, über S1 bzw. S2 verlaufenden Lichtwege von einem Punkte der Sternoberfläche bis zur Fokalebene äußerst genau übereinstimmen (bei Δλ=5 nm bis auf 0,01 mm), da sonst ein Wellenlängenunterschied ≈Δλ einen optischen Wegunterschied

λ zur Folge hat, der das Interferenzmuster zum Verschwinden bringt. Es werden so bei sehr großen Spiegelabständen extrem hohe Anforderungen an die mechanische Stabilität der Interferometerarme gestellt. Des weiteren wird eine äußerst präzise Mitführung des Instrumentes verlangt. Zweitens wird die Beobachtung des Interferenzbildes durch die atmosphärischen Szintillationen erschwert.

Die genannten Schwierigkeiten konnten in den fünfziger Jahren von R.H. Brown und R.Q. Twiss durch eine neuartige Nachweistechnik überwunden werden.

Das S. nach Brown und Twiss. Diese beiden Forscher ersetzten in der Michelsonschen Apparatur die beiden äußeren Planspiegel durch Reflektoren (Hohlspiegel), die das einfallende Sternlicht jeweils auf einen Photomultiplier fokussierten. Gemessen wurden Korrelationen zwischen den Photoströmen in der Weise, daß letztere nach schmalbandiger Verstärkung elektronisch miteinander multipliziert wurden. Der zeitliche Mittelwert dieses Produkts ergab das Meßsignal, das nichts anderes ist als die räumliche Korrelationsfunktion G⁽²⁾(r₁,r₂;0) (Korrelationsfunktionen des Strahlungsfeldes). Da die primären Meßgrößen (momentane) Intensitäten sind, befreit man sich so mit einem Schlage von allen mit Phasenänderungen bzw. -fluktuationen zusammenhängenden Störeinflüssen. Tatsächlich erhält man mit dem geschilderten Verfahren die gleiche Information wie beim Michelsonschen S. Dort wird nämlich auf dem Wege über die Sichtbarkeit des Interferenzbildes die Korrelationsfunktion G⁽¹⁾(r₁,r₂;0) (ihrem Betrage nach) gemessen (Interferenz), und wegen des für thermisches Licht gültigen Zusammenhanges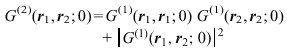


(2)

zwischen den Korrelationsfunktionen 1. und 2. Ordnung kann durch Messung von G⁽²⁾(r₁,r₂;0) ebenfalls |G⁽¹⁾(r₁,r₂;0)| bestimmt werden. G⁽²⁾(r₁,r₂;0) zeigt als Funktion des Abstandes d=|r₂-r₁| ein ausgeprägtes Maximum an der Stelle d=0 (der Kurvenverlauf ist ganz ähnlich wie beim photon bunching, Photonenstatistik), aus dessen Abfall der Sterndurchmesser ermittelt werden kann. Brown und Twiss bestimmten 1956 auf diese Weise den Durchmesser des Sirius. Später wurde in Narrabri (Australien) eine weiträumige Beobachtungsstation errichtet. Dort wurden die Reflektoren auf zwei Eisenbahnwagen montiert, die sich auf einem Schienenkreis mit einem Radius von 188 m bewegen können. Mit diesem Aufbau lassen sich Sterndurchmesser bis herab zu 0,0005″ messen.

Sterninterferometer: Michelsonsches Sterninterferometer. B Blende; S1, S2 verschiebbare Spiegel; S3, S4 feststehende Umlenkspiegel.