Lexikon der Physik: Atomspektrum
Atomspektrum, die Wellenlängen- bzw. Frequenzfolge, die durch die spektrale Zerlegung der von Atomen emittierten bzw. absorbierten elektromagnetischen Strahlung entsteht.
Die grundlegende Bedeutung der Analyse der Atomspektren für das Verständnis der Struktur der Atome formulierte Sommerfeld bereits 1919, also noch vor der Entwicklung der modernen Quantentheorie: "Seit der Entdeckung der Spektralanalyse konnte kein Kundiger zweifeln, daß das Problem des Atoms gelöst sein würde, wenn man gelernt hätte, die Sprache der Spektren zu verstehen. [...] Alle ganzzahligen Gesetze der Spektrallinien und der Atomistik fließen letzten Endes aus der Quantentheorie. Sie ist das geheimnisvolle Organon, auf dem die Natur der Spektralmusik spielt und nach dessen Rhythmus sie den Bau der Atome und Kerne regelt."
Ein Atom emittiert elektromagnetische Strahlung, wenn die Atomhülle von einem angeregten Zustand in einen energetisch niedriger liegenden Zustand oder in den Grundzustand übergeht. Die gebräuchlichsten Arten atomarer Anregung sind:
1) Thermische Anregung im elektrischen Lichtbogen bei Temperaturen von 6000 bis 8000°C oder im elektrischen Funken bei Temperaturen von 10000 bis 20000°C.
2) Fluoreszenzanregung, vor allem Resonanzfluoreszenzanregung, durch die Einstrahlung von absorptionsfähigem Licht, z.B. Laserlicht.
3) Stoßanregung durch Stöße mit Elektronen und anderen Atomen.
Bei verschieden starker Anregung entstehen unterschiedliche Spektren der gleichen Substanz: Im Lichtbogen erscheinen vorwiegend die Spektren der neutralen Atome, im Funkenspektrum hauptsächlich die Spektren ein- oder mehrfach ionisierter Atome. Man bezeichnet danach z.B. mit Fe I das Bogenspektrum des (neutralen) Eisenatoms; mit Fe II, III, ... die vom einfach, zweifach usw. ionisierten Eisenatom herrührenden Funkenspektren des Eisens. Es sind Funkenspektren bis zum Ionisationsgrad 20 und höher bekannt.
In den Frequenzen oder Wellenzahlen der Spektrallinien der Atome und Ionen lassen sich deutliche Gesetzmäßigkeiten erkennen, die die energetische Struktur der Atomhülle widerspiegeln. Beim Vergleich verschiedener Spektren gilt der spektroskopische Verschiebungssatz: Jedes Spektrum eines Ions vom Ionisationsgrad n ist im wesentlichen analog gebaut wie das Spektrum des Ions vom Ionisationsgrad n + 1 des nächsten Elements im periodischen System mit um 1 höherer Ordnungszahl, da der Charakter jedes Spektrums weitgehend durch die Zahl der Valenzelektronen des Atoms oder Ions bestimmt wird.
In den Spektren der Atome mit bis zu vier Valenzelektronen sind die Linien vorwiegend in Serien angeordnet. An die stärkste Linie mit niedrigster Wellenzahl schließt sich eine Folge von Linien mit wachsender Wellenzahl, aber abnehmender Intensität an, wobei der Wellenzahlabstand von Glied zu Glied kleiner wird. Diese Serie von Linien strebt einer echten Häufungsstelle am kurzwelligen Ende zu, der Seriengrenze. Jenseits der Seriengrenze liegt ein kontinuierliches Spektrum, das Seriengrenzkontinuum.
Einelektronenspektren: Die einfachste Struktur weisen die Spektren des Wasserstoffs, des einfach ionisierten Heliums und der weiteren Ionen mit nur einem einzigen Elektron auf, die weitgehend in den Röntgenbereich fallen (Röntgenspektrum, Wasserstoffspektrum). Die Wellenzahlen lassen sich mit großer Genauigkeit durch die Balmer-Formelλ-1 = RZ2(1/n2 – 1/m2) darstellen. Hierbei bedeuten R die Rydberg-Konstante, Z die Ordnungszahl und n und m ganze Zahlen 1, 2, 3,... Die Spektren der Einelektronensysteme lassen sich auf der Grundlage des Bohrschen Atommodells (Bohrsche Theorie) deuten, dem zufolge die Elektronen nur diskrete Energiewerte En,m annehmen können, zwischen denen Übergänge unter Emission oder Absorption von Licht gemäß der Bohrschen FrequenzbedingungEn – Em = hν möglich sind. Damit ergeben sich eine theoretische Ableitung der Balmer-Formel und ein Wert für die Rydberg-Konstante, der zahlenmäßig sehr gut mit dem empirisch gefundenen übereinstimmt. Bereits vor der Formulierung des Bohrschen Atommodells fand W. Ritz (1908), daß durch Addition und Subtraktion der Wellenzahlen zweier Spektrallinien eines Atoms meist die Wellenzahl einer weiteren Linie entsteht (Ritzsches Kombinationsprinzip). Die Größen Tn = – En/( ![]()
c) werden als spektroskopische Terme bezeichnet. Da die Energien En der gebundenen Zustände negativ sind, sind die zugehörigen Terme positiv. Eine graphische Darstellung der Energiezustände der Atome ist das Termschema, in dem die Terme nach ihrer Größe geordnet als horizontale Geraden aufgetragen sind (Abb. 1-3). Die Vertikalabstände der Geraden geben direkt die Wellenzahlen λ-1 der Spektrallinien wieder. Der tiefste Term mit n = 1 ist der Grundterm des Atoms (oder Ions), er hat den größten Termwert. Für n ![]()
∞ erreicht man die Termseriengrenze, die der Energie Null entspricht. Erfolgt die Anregung des Elektrons durch Licht der Frequenz ν, so wird die betreffende Linie absorbiert. Das Seriengrenzkontinuum entsteht durch einen Übergang des Elektrons aus einem gebundenen Zustand En in einen Zustand, bei dem es sich außerhalb des Atomverbands mit zusätzlicher kinetischer Energie bewegt.
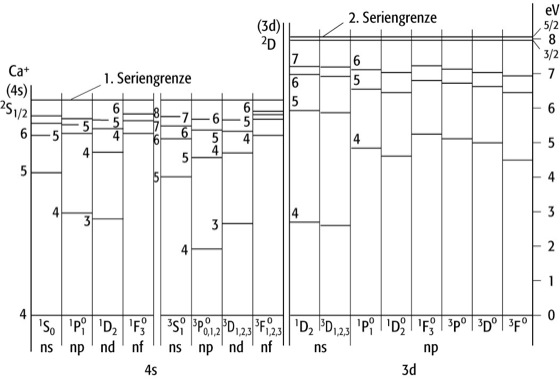
Spektren von Mehrelektronen-Atomen: Die Spektren der Atome oder Ionen mit mehreren Elektronen in der Hülle sind komplizierter als die Einelektronenspektren des Wasserstoffs und der wasserstoffähnlichen Ionen. Relativ einfach sind die Spektren der Atome oder Ionen mit nur einem Valenzelektron, bei denen also die Hülle ein Elektron zusätzlich zu einer Edelgaskonfiguration enthält: die Alkaliatome (Abb. 1), die einfach ionisierten Erdalkaliatome etc. Bei niedrigen Anregungsenergien bleibt der relativ stabile Atomrumpf mit seiner Edelgaskonfiguration praktisch unverändert, so daß sich nur die Zustände des Leuchtelektrons verändern, die aber dennoch eine größere Mannigfaltigkeit als die nur durch n gekennzeichneten Zustände des Wasserstoffspektrums bilden. Die durch die Hauptquantenzahl n festgelegten Terme spalten in n verschiedene Unterniveaus auf. Empirisch lassen sich diese Serien durch die Formeln

(Rydberg-Formel, α und β sind die Rydberg-Korrekturen) oder
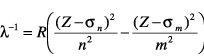
darstellen, wobei σn und σm Abschirmungskonstanten sind. Die allgemeinen Aussagen zum Wasserstoffspektrum (Kombinationsprinzip, Seriengrenze, Grenzkontinuum) bleiben voll gültig.
Im Rahmen der Quantenmechanik wird die Aufspaltung der n-Terme durch die Berücksichtigung des Bahndrehimpulses l ![]()
des Elektrons beschrieben. Für jedes n kann die Nebenquantenzahl l die Werte l = n – 1, ..., 0 annehmen, und es gibt zu jedem Wert von l eine besondere Termserie. Man bezeichnet die zu l = 0 gehörenden Terme mit dem Buchstaben s, zu l = 1 mit p, zu l = 2 mit d, zu l = 3 mit f usw. Die unter Lichtemission oder -absorption erfolgenden Übergänge gehorchen der Auswahlregel Δl = ± 1. Es gibt folgende wichtige Serien: 1s ![]()
np ist die Hauptserie; 2p ![]()
ns ist die scharfe Nebenserie; 2p ![]()
nd heißt diffuse Nebenserie; 3d ![]()
nf ist die Fundamentalserie (Bergmann-Serie).
In den Spektren von Atomen oder Ionen mit zwei Valenzelektronen (z.B. beim Helium oder Calcium, Abb. 2) gibt es mehrere Seriengrenzen; auf die Tatsache, daß diese Atome auch mehrere Termsysteme aufweisen, wird weiter unten eingegangen. Die erste Seriengrenze entspricht der Abtrennung des einen Leuchtelektrons von einem alkaliähnlichen Ion im Grundzustand als Ionisationsprodukt. Höher liegende Seriengrenzen sind auf Doppelanregungen zurückzuführen: Ein Elektron geht in die nächst höhere Anregungsstufe, während das andere Elektron seine Serie von Anregungszuständen bis zur Seriengrenze durchläuft. Das Ionisationsprodukt ist jetzt ein Alkaliion in einem angeregten Zustand. Auf diese Weise entstehen diskrete Anregungszustände des Atoms jenseits der ersten Ionisationsgrenze (negative Terme). Ähnliche höhere Seriengrenzen gibt es auch in anderen Spektren. Tabelle 1 zeigt als weiteres Beispiel für Atome mit zwei Valenzelektronen die Termwerte des Quecksilberatoms.
Atomspektrum 1: Termwerte des Quecksilberatoms.
| |||
| 1 184,96 nm | 1 546,07 nm | 1 253,65 nm | |
| 2 1013,98 nm | 2 435,83 nm | 2 578,97 nm | |
| 3 491,60 nm | 3 404,66 nm | 3 576,96 nm | |
| 4 579,07 nm | 4 296,73 nm | ||
| 5 434,75 nm | 5 313,16 nm | ||
| 6 1691,83 nm | 6 312,57 nm | ||
| 7 366,29 nm | |||
| 8 365,48 nm | |||
| 9 365,01 nm |
Feinstruktur: Im allgemeinen sind die Atomspektren bedeutend komplizierter als bisher dargestellt; dazu tragen folgende Faktoren bei (Atomtheorie):
1) die Coulomb-Wechselwirkung der Elektronen;
2) relativistische Korrekturen;
3) quantenelektrodynamische Strahlungskorrekturen;
4) Wechselwirkungen der Elektronen mit den Freiheitsgraden des Atomkerns (Hyperfeinwechselwirkungen).
Die relativistischen Korrekturen führen gemeinsam mit magnetischen Wechselwirkungen, die mit dem magnetischen Eigenmoment (Spinmoment) der Elektronen verknüpft sind, zur Feinstruktur der Atomspektren und umfassen bei einer Störungsrechnung erster Ordnung in ![]()
2/c2 hauptsächlich die Spin-Bahn- und Spin-Spin-Wechselwirkungen. Der größte Beitrag ist in der Regel die Wechselwirkung zwischen Bahnmoment und Spin des selben Elektrons; dieser Term ist in den meisten Fällen gemeint, wenn von Spin-Bahn-Kopplung gesprochen wird. Für die schwersten Atome (etwa ab Rubidium) werden auch die anderen relativistischen Effekte so groß, daß die Beiträge erster Ordnung oft nicht mehr ausreichen oder eine Störungsrechnung sogar überhaupt nicht mehr anwendbar ist. Die Berücksichtigung der endlichen Masse und Ausdehnung des Kerns sowie der Wechselwirkung der Elektronen mit den elektrischen und magnetischen Kernmomenten führt schließlich zur Hyperfeinstruktur.
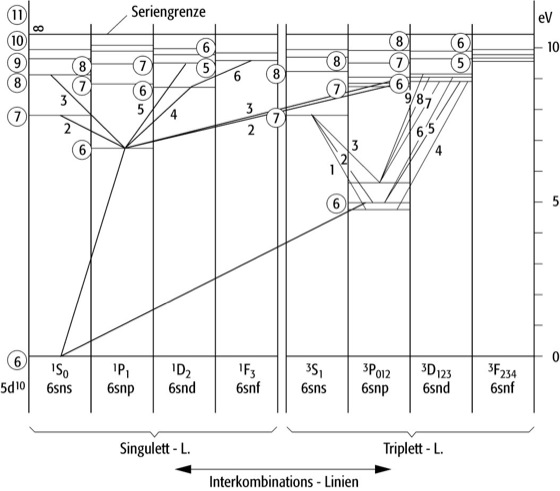
Die Feinstruktur äußert sich in der Multiplizität der Spektren. Bei den Spektren von Atomen mit einem Valenzelektron außerhalb einer abgeschlossenen Schale, also den Alkalien, und auch bei solchen Elementen, bei denen ein Elektron zum Schalenabschluß fehlt, den Halogenen, sind bei entsprechender experimenteller Auflösung alle Einzellinien als eng beieinanderliegende Doppellinien zu erkennen; man spricht daher von Dublettspektren. Bei diesen Atomen sind alle Zustände mit l > 0 verdoppelt, es existiert genau ein Termsystem, das Dublettsystem. Bei den zweiwertigen Elementen, die entweder zwei Elektronen außerhalb der Edelgasschale haben, den Erdalkalimetallen und Elementen der II. Nebengruppe, oder bei denen zwei Elektronen zu einer abgeschlossenen Schale fehlen, den Chalkogenen, gibt es zwei voneinander unabhängige Termsysteme: das Singulettsystem, das aus einfachen Zuständen besteht, und das Triplettsystem, das bei allen Zuständen außer den s-Zuständen eine Feinstruktur von je drei Zuständen zeigt (Abb. 3).
Im Verlauf der Zunahme der Zahl der äußeren Elektronen der Elemente im Periodensystem findet man folgende, als Multiplizitäten bezeichnete Aufspaltungen der einzelnen Terme:
| |||||||||
| Multiplizität | 2 | 1, 3 | 2, 4 | 1, 3, 5 | 2, 4 | 1, 3 | 2 | 1, 3 |
Es wechseln also geradzahlige und ungeradzahlige Multiplizitäten miteinander ab (spektroskopischer Wechselsatz). Mit Annäherung an eine Edelgasschale nehmen die auftretenden maximalen Multiplizitäten wieder ab.
DrehimpulskopplungundTermsymbolik: Im allgemeinen Fall, also bei mehr als einem Elektron, verwendet man zur Kennzeichnung der Feinstrukturniveaus und der zwischen ihnen auftretenden Strahlungsübergänge folgende drei Quantenzahlen: die Spinquantenzahl S des resultierenden Spindrehimpulses, die Drehimpulsquantenzahl L des resultierenden Bahndrehimpulses und die Gesamtdrehimpulsquantenzahl J.
Dies hat zur Voraussetzung, daß für die vektorielle Addition des Bahndrehimpulses und des Spins die sogenannte Russell-Saunders-Kopplung, auch LS-Kopplung genannt, gültig ist (Drehimpuls). Wie sich anhand experimenteller Untersuchungen zeigen läßt, trifft dies auf die meisten Atome – in Strenge allerdings nur für alle nicht zu schweren Atome – zu. Bei diesem Kopplungstyp ist die Wechselwirkung aller Bahndrehimpulse li der Elektronen und diejenige aller Spins si untereinander groß gegenüber der Wechselwirkung zwischen Bahndrehimpuls und Spin eines einzelnen Elektrons. So setzen sich zunächst die Bahndrehimpulse aller (äußeren) Elektronen zum resultierenden Bahndrehimpuls L, der den Termcharakter (Kennzeichnung mit Großbuchstaben S, P, D, F etc.) bestimmt, zusammen, und die Spins der Elektronen addieren sich dazu analog zum Gesamtspin S der Atomhülle. L und S schließlich addieren sich vektoriell zum Gesamtdrehimpuls J des Atoms.
Ein zweiter Drehimpulskopplungsytp, die sogenannte jj-Kopplung, tritt hauptsächlich bei den angeregten Zuständen schwerer Atome auf. Hier ist die Wechselwirkung zwischen Bahndrehimpuls und Spin der einzelnen Elektronen so groß, daß sich zunächst beide zu den Gesamtdrehimpulsen ji der Einzelelektronen zusammensetzen, die sich dann zum resultierenden Drehimpuls J des gesamten Atoms aufsummieren. Bei der jj-Kopplung gibt es also keinen Gesamt-Bahndrehimpuls L mehr, und damit entfällt auch die Möglichkeit, einen Term durch ein Symbol S, P, D, F, etc. zu kennzeichnen. LS- und jj-Kopplung führen zur gleichen Gesamtzahl der Feinstrukturterme, sie unterscheiden sich jedoch in der relativen Termlage. Im folgenden betrachten wir ausschließlich den Fall der LS-Kopplung und erläutern die sogenannte Termsymbolik.
Für bestimmte Werte von L und S durchläuft J alle Werte von L + S bis L – S, wobei sich benachbarte Werte um 1 unterscheiden und zu verschiedenen Werten der Spin-Bahn-Wechselwirkungsenergie gehören. Für S ≤ L gibt es 2S + 1, sonst 2L + 1 verschiedene J-Werte; demgemäß wird (für L S eigentlich unzutreffend) 2S + 1 allgemein als Multiplizität, mitunter auch als permanente Multiplizität bezeichnet. Im Singulettsystem ist S = 0, also J = L. Im Dublettsystem ist S = 1/2. Aus L und S bildet man dann die Werte
| ||||||
| J = 1/2 | 1/2, 3/2; | 3/2,5/2; | 5/2, 7/2; | 7/2, 9/2; | usw. |
Im Triplettsystem ist S = 1; hier gilt
| ||||||
| J = 1 | 0,1,2 | 1,2,3 | 2,3,4 | 3,4,5 | usw. |
Im Termsymbol wird die Multiplizität 2S + 1 oben links, der Wert von J unten rechts an die den verschiedenen L-Werten L = 0, 1, 2, ... zugeordneten Buchstaben S, P, D, angeschrieben, also z.B. 3D2 für S = 1, L = 2, J = 2.
Die magnetische Wechselwirkungsenergie bei einem Elektron ist proportional zu ls, bei mehreren Elektronen proportional zu
.
Dabei ergibt sich diese Darstellung für LS durch die Quantenzahlen J, L und S aus J2 = (L + S)2, J2 = ![]()
J(J + 1) und entsprechenden Gleichungen für L2 und S2. Da L und S konstante Werte haben, sind die Energiedifferenzen innerhalb des Multipletts proportional zu den Differenzen von J(J + 1). Für energetisch benachbarte Zustände ist ΔJ = 1, also Δ[J(J + 1)] = J(J + 1) – (J – 1)(J – 1 + 1) = 2J Daraus folgt die Landésche Intervallregel: Die Energie- bzw. Wellenzahlabstände benachbarter Terme eines Termmultipletts sind proportional zur größeren der beiden Quantenzahlen J.
Für die Reihenfolge der Feinstrukturterme gilt: Im allgemeinen liegt die Energie mit dem niedrigsten J am tiefsten (größte Ablösungsarbeit des Elektrons). Dies bezeichnet man als normale Termordnung. Die umgekehrte Ordnung tritt bei Termstörungen auf oder wenn statt 1, 2, ... Elektronen ebensoviele Löcher in abgeschlossenen Edelgasschalen die Termstruktur bedingen (z.B. Halogene und Chalkogene).
Über die Lage von Termgruppen gibt die Hundsche Regel Auskunft: Von den möglichen Multiplizitäten (Singuletts, Tripletts, u.a.) einer Elektronenkonfiguration liegt die Gruppe der höchsten Multiplizität am tiefsten; von den verschiedenen möglichen L-Zuständen liegen die mit dem größten L am tiefsten.
Von besonderem Interesse ist der Grundzustand des Atoms. Die spektroskopisch nachgewiesenen Grundzustände der ersten Elemente des Periodensystems zeigt Tabelle 2.
Atomspektrum 2: Spektroskopisch nachgewiesene Grundzustände der ersten Elemente des Periodensystems.
| |||
| 1 | H | 1s1/2 | |
| 2 | He | 1s0 | |
| 3 | Li | 2s1/2 | |
| 4 | Be | 1s0 | |
| 5 | B | 2p1/2 | |
| 6 | C | 3p0 | |
| 7 | N | 4s3/2 | |
| 8 | O | 3p2 | |
| 9 | F | 3p3/2 | |
| 10 | Ne | 1s0 |
Auswahlregeln: Bereits bei den einfachen Spektren eines einzigen Leuchtelektrons wird die Gesamtheit der Spektrallinien durch die atomaren Energieniveaus und die gültigen Auswahlregeln für Strahlungsübergänge bestimmt, durch die eine Vielzahl von energetisch durchaus möglichen Übergängen verboten werden. Diese Verbote folgen aus weiteren Erhaltungssätzen, nämlich für Gesamtdrehimpuls und Parität des Systems einschließlich des emittierten oder absorbierten Photons. Angeregte Zustände, die aufgrund der Auswahlregeln weder direkt noch indirekt mit dem Grundzustand kombinieren, werden als metastabile Zustände bezeichnet. Für die elektrische Dipolstrahlung, dem bei atomaren und molekularen Systemen (im Gegensatz zu Atomkernen) allein wesentliche Strahlungstyp, lauten die Auswahlregeln:
1) Für erlaubte Übergänge ist die Differenz ΔJ zwischen den Drehimpulsquantenzahlen der beiden miteinander kombinierenden Zustände 0, + 1 oder – 1, wobei Übergänge zwischen zwei Zuständen mit J = 0 verboten sind.
2) Für erlaubte Übergänge müssen die miteinander kombinierenden Atomzustände verschiedene Parität haben (Laportesche Auswahlregel). Die Parität bei einem einzelnen Elektron wird durch seinen Bahndrehimpuls l bestimmt; sie ist gerade, falls l gerade ist, und ungerade, falls l ungerade ist. Entsprechend bestimmt L die Parität des Gesamtzustandes der Elektronenhülle. Zur Kennzeichnung der Parität setzt man bei ungeraden Termen ein kleines o (von engl. odd "ungerade") oben rechts an das Termsymbol, z.B. ![]()
, während die geraden Terme nicht extra gekennzeichnet werden.
3) Das Umklappen eines Elektronenspins ist, auch bei Änderung der übrigen Quantenzahlen, sehr unwahrscheinlich. Dies führt zum Interkombinationsverbot, dem zufolge Übergänge zwischen Termsystemen verschiedener Multiplizitäten verboten sind.
Die Auswahlregeln gelten nicht bei anderen Prozessen, etwa bei der Anregung von Atomen durch Stöße.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.