Clusterphysik

Oliver Rattunde und Hellmut Haberland, Freiburg i. Brsg.

Bis vor wenigen Jahren gab es kaum Berührungspunkte zwischen der Physik der Atome und Moleküle und der Physik der kondensierten Materie. Erst in den späten 70er Jahren begann, was heute als Clusterphysik bezeichnet wird: die systematische Untersuchung einer Ansammlung von einigen wenigen (N = 4, 5, 6,...) bis hin zu mehreren zehntausend Atomen bzw. Molekülen, den sog. Clustern. Damit konnte eine Brücke zwischen den bisher getrennten Gebieten geschlagen werden.

Im Prinzip versucht die Clusterphysik, alle relevanten physikalischen und chemischen Eigenschaften der Materie als Funktion der Clustergröße, d.h. der Anzahl der Atome in einem Cluster, zu beschreiben. Typische Fragestellungen sind: Wie fängt ein Kristall an zu wachsen? Wie entwickelt sich aus der Ionisierungsenergie des Atoms oder Moleküls die Austrittsarbeit des Festkörpers? Ab welcher Clustergröße tritt Ferromagnetismus auf? Wie entwickelt sich aus dem magnetischen Moment des Atoms der Magnetismus des Festkörpers? Was bedeutet eigentlich Temperatur oder Schmelzen bei endlichen Systemen? Wie sind die katalytischen Eigenschaften? Diese Liste ließe sich beliebig verlängern.

Bei diesen Untersuchungen stellte es sich heraus, daß alle physikalischen und chemischen Eigenschaften von der Clustergröße abhängen. Das macht das Gebiet einerseits wissenschaftlich sehr interessant, andererseits ergeben sich Anwendungen in der Nanotechnologie, da man mit der Clustergröße einen Parameter in der Hand hat, mit dem man physikalische oder chemische Eigenschaften kontrolliert einstellen kann.

Eine grobe Einteilung der Cluster wird in der Regel anhand ihrer Größe vorgenommen:

- sehr klein: Die Anzahl der Atome pro Cluster ist N = 3 bis 10 oder 13. Für N ≤ 12 sind noch alle Atome an der Oberfläche. Die Konzepte und Methoden der Molekülphysik sind anwendbar. Physikalische Eigenschaften ändern sich oft sprunghaft mit N.

- klein: N = 10 oder 13 bis etwa 100. Es existieren viele isomere Strukturen mit ähnlicher Bindungsenergie. Molekulare Konzepte verlieren ihre Brauchbarkeit.

- mittel: N = 100 bis etwa 1000 oder 10 000. Einige – aber nicht alle – Eigenschaften streben langsam gegen ihren asymptotischen Wert.

- groß: N größer als etwa 10 000. Man spricht auch von kleinen Teilchen oder Mikrokristallen. Die Eigenschaften entwickeln sich gleichmäßig zu denen des Festkörpers.

Erste Experimente mit Clustern wurden schon vor 3500 Jahren in Ägypten durchgeführt, als man lernte, durch Zugabe von Metalloxiden Gläser oder Glasuren von Keramiken zu färben. Beim Erhitzen beginnen die Metallatome im Glas zu diffundieren und sich zu Clustern zusammenzulagern. Je nach Temperatur und Länge der Wärmebehandlung entstehen so unterschiedlich große Metallcluster. Mit Silber z.B. kann Glas von gelb über rot, violett, blau bis grau-grün gefärbt werden, wenn sich die Größe der Silbercluster von 0,1 bis 1,3 μm verändert. Dieses Phänomen kann im Rahmen der klassischen Mie-Theorie durch eine größenabhängige Plasmonresonanz der Metallelektronen erklärt werden. Dieses Beispiel zeigt schön, wie über die Größe eine physikalische Eigenschaft – hier die Farbe – eingestellt werden kann.

Man kann die Untersuchungen an Clustern grob in zwei Gruppen einteilen: 1) Untersuchungen an freien Clustern, bei denen Eigenschaften von Clustern im Vakuum untersucht werden, und 2) Studien an Clustern auf Oberflächen, bzw. Clustern, die mit Oberflächen wechselwirken (z.B. an ihnen gestreut werden) oder in andere Materialien eingelagert werden. Bei den ersteren handelt es sich fast immer um grundlegende Untersuchungen, während im letzteren Fall oft Anwendungen im Vordergrund stehen.

Untersuchungen an freien Clustern

Das Schema einer einfachen Apparatur zur experimentellen Untersuchung von Clustern zeigt Abb. 1 . Unter der Vielzahl von Clusterquellen ist die Laserverdampfungsquelle besonders populär geworden.

Mit einer derartigen Quelle wurde z.B. das in Abb. 2 dargestellte Massenspektrum von Kohlenstoff-Clustern erzeugt. Das Clusterwachstum kann durch Variation der Bedingungen in der Clusterquelle so beeinflußt werden, daß fast ausschließlich

zu sehen ist. Dessen fußballähnliche Struktur war zu Anfang heftig umstritten, wurde aber in einer Vielzahl von Experimenten und Rechnungen bestätigt. Es gibt eine ganze Reihe ähnlicher, hohler Kohlenstoffcluster (C₆₀, C₇₀, usw.), die sog. Fullerene. Für ihre Entdeckung und Untersuchung wurden R. E. Smalley, R. F. Curl und H. W. Kroto 1996 mit dem Nobelpreis für Chemie ausgezeichnet.

Abb. 3 zeigt ein weiteres Beispiel dafür, wie man in der Frühzeit der Clusterphysik mit einer einfachen Apparatur, wie Abb. 1 sie zeigt, interessante physikalische Ergebnisse erzielen kann. Dargestellt ist ein Massenspektrum heißer Natrium-Cluster. Die Cluster haben durch den Produktionsprozeß eine so hohe innere Anregung erhalten, daß sie zwischen Clusterquelle und Massenspektrometer Atome abdampfen. Für schwächer gebundene Cluster ist diese Abdampfung wahrscheinlicher, so daß ihre Intensität im Massenspektrum abnimmt und sich auf den stärker gebundenen Clustern ansammelt. Aus der hohen Intensität einiger Massen, z.B. denen mit 2, 8, 20 oder 40 Atomen pro Cluster, läßt sich also auf ihre höhere Stabilität gegenüber Abdampfen von Atomen und damit auch auf eine höhere atomare Bindungsenergie schließen.

Das Massenspektrum in Abb. 3 war der erste experimentelle Hinweis auf ein Modell, das nicht nur für Alkali-Cluster, sondern auch für alle Metalle von großer Bedeutung ist: das Modell des quasifreien Elektronengases, auch Jellium-Modell genannt. Das Modell ist verblüffend erfolgreich, wenn man bedenkt, mit welcher einfachen Annahme es auskommt: Die Coulomb-Wechselwirkung zwischen Elektronen und Kernen wird gleichmäßig (wie Marmelade, amerikanisch: jelly) ausgestrichen. Nur die Coulomb-Wechselwirkung der Elektronen untereinander wird vollständig berücksichtigt.

Es gab verschiedene Versuche, die optische Absorption mit einer Apparatur nach Abb. 1 zu messen. Dies ist heute aber fast ganz aufgegeben worden, da es zu einer charakteristischen Schwierigkeit kommt: Bei der Photoabsorption und der nachfolgenden, zum Nachweis notwendigen Ionisation bleibt der Cluster nur ganz selten intakt. Meist dampft er einige Atome oder auch größere Bruchstücke ab. In einer Apparatur nach Abb. 1 führt dieser auch Fragmentation genannte Prozeß dazu, daß man die gemessenen Signale im Massenspektrum nicht eindeutig einer definierten Clustergröße zuordnen kann. Man benötigt also eine zusätzliche Massenanalyse vor der Wechselwirkung mit den Photonen. Nun ist die Massentrennung neutraler Cluster schwierig und apparativ aufwendig, so daß meistens mit positiv oder negativ geladenen Ionen gearbeitet wird, wie in Abb. 4 schematisch wiedergegeben ist.

Abb. 4 zeigt noch eine Besonderheit: Es kann mit Clustern definierter Temperatur gearbeitet werden. Dazu schickt man die Cluster durch ein verdünntes Helium-Gas bekannter Temperatur. Durch die vielen Stöße mit den Helium-Atomen nehmen die Cluster eine kanonische Temperaturverteilung an, bei der sie im zeitlichen Mittel mit dem Gas keine Energie austauschen.

Abb. 5 zeigt Photoabsorptionsquerschnitte und relevante geometrische Strukturen für

und

. Diese Cluster haben 8 bzw. 10 Valenzelektronen, und da es im Jellium-Modell nur auf die Anzahl der Elektronen ankommt, ist

ein kugelsymmetrischer magischer Cluster (ebenso wie Na₈ und

) und

nicht. Daher sollte man für

eine und für

zwei oder drei intensive Absorptionslinien erwarten. Diese sieht man auch, aber nur bei so hohen Temperaturen, daß die Cluster flüssig sind. Die energetische Lage der Maxima läßt sich gut im Jellium-Modell berechnen, die Breite der Linien ist allerdings noch nicht ganz verstanden.

Bei tiefen Temperaturen (T = 35 K) sehen die Spektren anders aus: Man beobachtet zwei bzw. fünf schmalere Maxima ( Abb. 5 ). Bei tiefen Temperaturen führen die Atome nur noch kleine Schwingungen um die Gleichgewichtslage aus, der Cluster verhält sich also wie ein großes Molekül mit einer festen geometrischen Struktur. Entsprechend interpretiert man die Linien in Abb. 5b als nicht aufgelöste elektronische Übergänge in einem kalten

-Molekül.

Bei der Beschreibung der optischen Spektren ändert sich also die Art des physikalischen Konzeptes mit der Temperatur. Bei tiefen Temperaturen, wenn die Atome im Cluster noch nicht beweglich sind, verwendet man Konzepte der Molekülphysik, bei hohen Temperaturen findet das aus der Festkörperphysik stammende Jellium-Modell seine Anwendungen. Es sind heute Bestrebungen im Gange, das Jellium-Modell so zu erweitern, daß es auch gestattet, die kleinen, kalten Cluster zu berechnen. Genauso werden z.Zt. die ersten molekülphysikalischen Rechnungen für heiße Cluster gemacht. Durch diesen doppelten Zugang hat sich eine Breite der theoretischen Beschreibung ergeben, die zu tieferen Einsichten geführt hat.

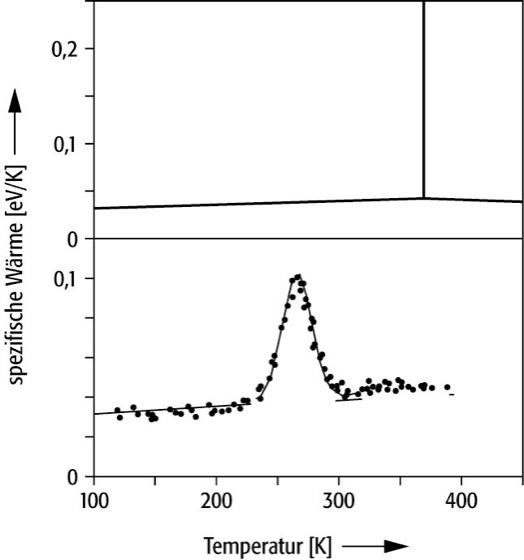
Neben den optischen lassen sich auch thermische Eigenschaften massenselektierter Cluster messen. Abb. 6 zeigt als Beispiel die spezifische Wärme von

. Diese ist definiert als Ableitung der inneren Energie U = U(T) nach der Temperatur T:

. Mit einer Apparatur nach Abb. 4 ist es möglich, Cluster definierter Temperatur T herzustellen. Zur Messung deren innerer Energie U benutzt man die Tatsache, daß das Fragmentationsmuster eines Clusters stark von dessen innerer Energie abhängt.

Die Alkalimetalle sind theoretisch besonders einfach zu beschreiben. Die für sie entwickelten Ideen sind aber oft auch auf andere Metalle anwendbar. Wie groß die Ähnlichkeit der verschiedenen Metalle sein kann, zeigt Abb. 7 . Aufgetragen ist die Differenz aus Ionisierungsenergie (IE) bzw. Elektronenaffinität (EA) und der Austrittsarbeit des Festkörpers. Die beiden Energien IE und EA werden benötigt, um ein Elektron von einem neutralen bzw. negativ geladenen Cluster zu entfernen:

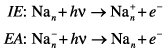
Cluster und Oberflächen

Bei einem typischen Experiment zur Untersuchung der Wechselwirkung von Clustern mit Oberflächen wird ein Clusterstrahl auf eine Oberfläche gerichtet und entweder die Streuung der Cluster an der Oberfläche oder häufiger die Eigenschaften der deponierten Cluster auf der Oberfläche studiert. Wichtig ist, wie bei vielen Experimenten der Oberflächenphysik, daß der Zustand der Oberfläche genau bekannt ist. Deshalb werden diese Experimente oft im Ultrahochvakuum durchgeführt. Aus der Vielfalt der Experimente soll hier nur eines diskutiert werden, bei dem die Oberflächendiffusion als Funktion der Clustergröße untersucht wurde.

Abb. 8 zeigt Transmissionselektronenmikroskopie-Aufnahmen von Antimon(Sb)-Inseln auf Graphit. Dazu wurden neutrale Sb-Cluster mit einer mittleren Größe von 4, 90 bzw. 240 Atomen pro Cluster mit geringer kinetischer Energie auf einer Graphit-Oberfläche (T = 300 K) deponiert. Sb-Cluster aller drei Größen sind bei Zimmertemperatur auf Graphit sehr beweglich und lagern sich zu unterschiedlich strukturierten Inseln zusammen. Man erkennt, daß sich kleine Cluster (N = 4) zu größeren Inseln mit kompakter Struktur zusammenlagern, wie dies auch bei der Oberflächendiffusion einzelner Atome beobachtet wird. Mit zunehmender Größe der auftreffenden Cluster ändert sich dieses Verhalten, und es entstehen neue, fraktale Strukturen auf der Oberfläche (Fraktale).

Anwendungen

Eine der Faszinationen der Clusterphysik besteht darin, daß sich aus grundlegenden Untersuchungen interessante Anwendungen ergeben können:

Die Firma IBM hat ein Verfahren entwickelt, bei dem ein Strahl sehr großer Argon-Cluster zum Reinigen von Halbleiterwafern benutzt wird. (Die Cluster sind so groß, daß IBM nicht von Clustern, sondern von Aerosolen spricht.) Die mit einer gekühlten Düsenstrahlquelle (Clusterquelle) erzeugten Ar-Cluster prallen unter 45° auf die Halbleiterstruktur und entfernen so kleine Staubpartikel, die hochintegrierten Chips gefährlich werden können.

Man kann die Erosionswirkung verstärken, indem man die Cluster ionisiert und dann elektrisch beschleunigt. Damit läßt sich nicht nur Staub entfernen, sondern die Oberfläche kann gezielt abgetragen oder geglättet werden. Derartige Verfahren werden z.Zt. in verschiedenen Labors für den industriellen Einsatz getestet und vorbereitet. Angeblich werden sie in Japan bereits eingesetzt, um komplizierte Brillengläser zu bearbeiten. Diese Form der Clustererosion beruht darauf, daß man Cluster aus Materialien verwendet, die bei Zimmertemperatur gasförmig sind. Richtet man hingegen einen Strahl aus metallischen Clustern auf eine Oberfläche, so verbinden sich diese bei Aufprall mit der Oberfläche (Clusterbeschichtung). Bei hoher Auftreffenergie der Cluster können auf diese Weise extrem glatte und gut haftende Schichten hergestellt werden.

Ein weiteres wichtiges Anwendungsgebiet ist die Katalyse, also die Aktivierung oder Beschleunigung chemischer Prozesse. Fast alle industriell eingesetzten Katalysatoren sind feinst verteilte Pulver auf einer chemisch inerten Unterlage. Da die Adsorptionswahrscheinlichkeit eines Moleküls auf einem Partikel (also der erste katalytische Schritt) stark von dessen Größe abhängt, ergeben sich vielfältige Möglichkeiten für Katalysatoren, die aus oder mit Clustern gefertigt werden.

Als C₆₀ zum ersten Mal in größeren Mengen produziert wurde, gab es unzählige Vorschläge für dessen Anwendung, von atomaren Kugellagern bis hin zu Behältern für die Endlagerung radioaktiver Atome (Fullerene). Davon ist bisher industriell noch nichts verwirklicht worden. Das gleiche gilt für die kleinen Fullerenröhren (engl. carbon nano tubes oder Buckyballs).

Der berühmte theoretische Physiker R. Feynman hat einmal geschrieben: "There is plenty of room at the bottom", wobei er meinte, daß man vieles noch viel kleiner bauen und konstruieren könnte. Diese Worte sind zum Motto der Nanotechnologie geworden. In diesem Wettlauf hin zu immer kleineren Strukturen wird die Clusterphysik eine wichtige Rolle spielen, sobald die Nanotechnologie in Größenbereiche vorstößt, bei denen sich physikalische oder chemische Eigenschaften der Materie als Funktion der Anzahl der verwendeten Atome oder Moleküle verändern.

Clusterphysik 1: Schema einer einfachen Apparatur zur Untersuchung von Clustern. Diese werden in einer Clusterquelle (CQ) erzeugt und treten durch eine konische Blende in eine separat bepumpte Kammer. Dort können sie durch Elektronen- oder Photonenbeschuß ionisiert, in einem Massenspektrometer (MS) nach Massen getrennt und in einem Detektor (D) nachgewiesen werden. Zwei Pumpen (P) sorgen für ein ausreichendes Vakuum.

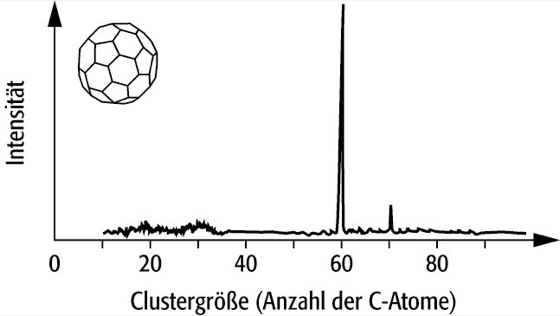
Clusterphysik 2: Dieses Massenspektrum von Kohlenstoff-Clustern wurde mit einer Apparatur wie in Abb. 1 aufgenommen. Variiert man die Bedingungen in der Clusterquelle, so ändert sich die Form des Massenspektrums. Aus der herausragenden Intensität bei Masse 720 (dies entspricht genau 60 C-Atomen) wurde auf die ungewöhnliche Stabilität des C₆₀ geschlossen.

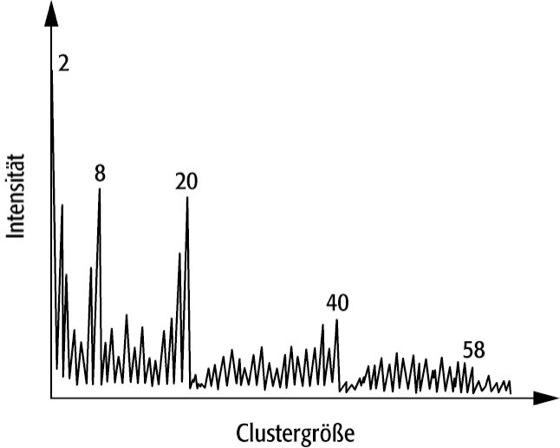
Clusterphysik 3: Massenspektrum heißer Natrium-Cluster. Einige Massen, die mit 2, 8, 20, 40 Atomen, haben eine höhere Intensität, für die der Begriff magische Cluster gebraucht wird. Bei heißen Clustern gibt es eine Korrelation zwischen höherer Intensität im Massenspektrum und größerer Bindungsenergie, d.h. höherer Stabilität des Clusters, die für Natrium im Rahmen des Jellium-Modells erklärt werden kann.

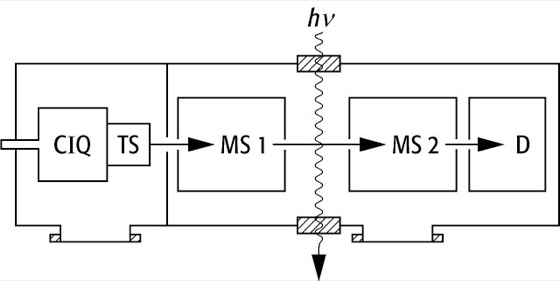
Clusterphysik 4: Schema einer Apparatur zur Untersuchung von optischen und thermischen Eigenschaften geladener Cluster. Die in der Clusterionenquelle (CIQ) erzeugten elektrisch geladenen Cluster nehmen in der Thermalisierungsstufe (TS) eine definierte Temperatur an. Im ersten Massenspektrometer (MS1) wird eine einzige Clustergröße selektiert, anschließend mit Licht aus einem Laser bestrahlt und die Photoprodukte in einem zweiten Massenspektrometer (MS2) getrennt. Durch die Massenselektion von MS1 wird das Problem der Fragmentation umgangen.

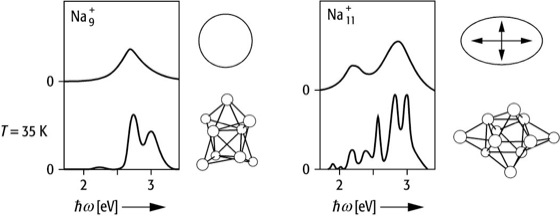
Clusterphysik 5: Optisches Absorptionsspektrum für feste (links, 35 K) und flüssige (rechts)

– und

-Cluster. Aufgetragen ist der Absorptionsquerschnitt pro Valenzelektron gegen die Photonenergie

in eV. Bei hohen Temperaturen zeigen sich breite Strukturen, deren Maxima sich gut durch eine im Jellium-Modell kugelförmige (

, links bzw. asphärische (

, rechts) Elektronenverteilung erklären lassen. Bei tiefen Temperaturen erhält man nicht aufgelöste elektronische Molekülbanden. Die Geometrie der festen Cluster und des entsprechenden Jellium-Tropfens ist rechts gezeichnet.

Clusterphysik 6: Vergleich der spezifischen Wärme des Na-Festkörpers (oben) mit der von

(unten). Die δ-funktionsartige Singularität am Schmelzpunkt verbreitert sich für endliche Systeme, und der Schmelzpunkt sinkt um etwa 20 bis 30 %.

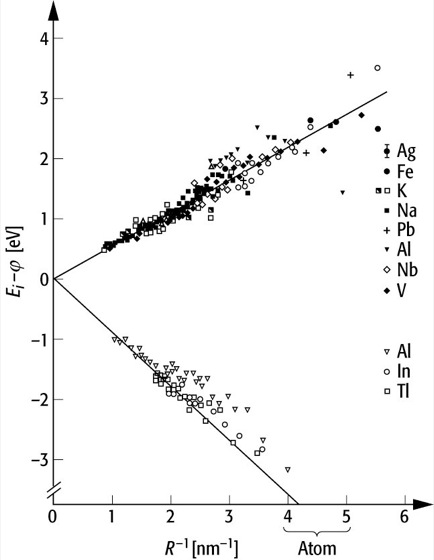
Clusterphysik 7: Größenabhängigkeit von Ionisierungsenergie (IE) und Elektronenaffinität (EA). Aufgetragen ist die Differenz IE – ϕ bzw. ϕ – EA, wobei ϕ die Austrittsarbeit des Festkörpers ist, gegen den reziproken Radius des als kugelförmig angenommenen Clusters. Beide Werte konvergieren für große Clusterradien R, d.h. R ^{- 1}

0, linear gegen den Wert der Austrittsarbeit des jeweiligen Festkörpers. Die Steigungen der eingezeichneten Geraden von ± e²/2 entsprechen dem Verlauf des klassischen Coulomb- und Bildladungspotentials für eine metallische Kugel mit Radius R. Die Abweichung der Meßpunkte von den Geraden wird auf quantenmechanische Effekte zurückgeführt.

Clusterphysik 8: Strukturen von Antimon-Inseln auf einer Graphitoberfläche. Werden Antimon-Cluster unterschiedlicher Größe bei Raumtemperatur auf Graphit deponiert, ergeben sich je nach Clustergröße Antimon-Inseln unterschiedlicher Struktur. In allen drei Fällen wurde die gleiche Menge Atome – jeweils eine Monolage – deponiert. Die Größe der Cluster bestimmt die Art der Oberflächendiffusion und somit die Struktur der Inseln.